个人主页：点我进入主页
专栏分类：C语言初阶 C语言进阶 数据结构初阶 Linux C++初阶 C++进阶 算法
欢迎大家点赞，评论，收藏。
一起努力，一起奔赴大厂
目录
一.二叉搜索树概念
二.实现
2.1插入
2.2遍历
2.3查找
2.4删除
2.4.1删除节点的左子树为空
2.4.2删除节点的右子树为空
2.4.3删除节点的左子树和右子树都不为空
编辑2.4.4代码
三.K-V模型
四.二叉搜索树的性能分析
一.二叉搜索树概念
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:若它的左子树不为空，则左子树上所有节点的值都小于根节点的值若它的右子树不为空，则右子树上所有节点的值都大于根节点的值它的左右子树也分别为二叉搜索树。
二.实现
2.1插入
插入遵循二叉树的规则，左子树都比父节点小，右子树都比父节点大，我们可以看下面图片：
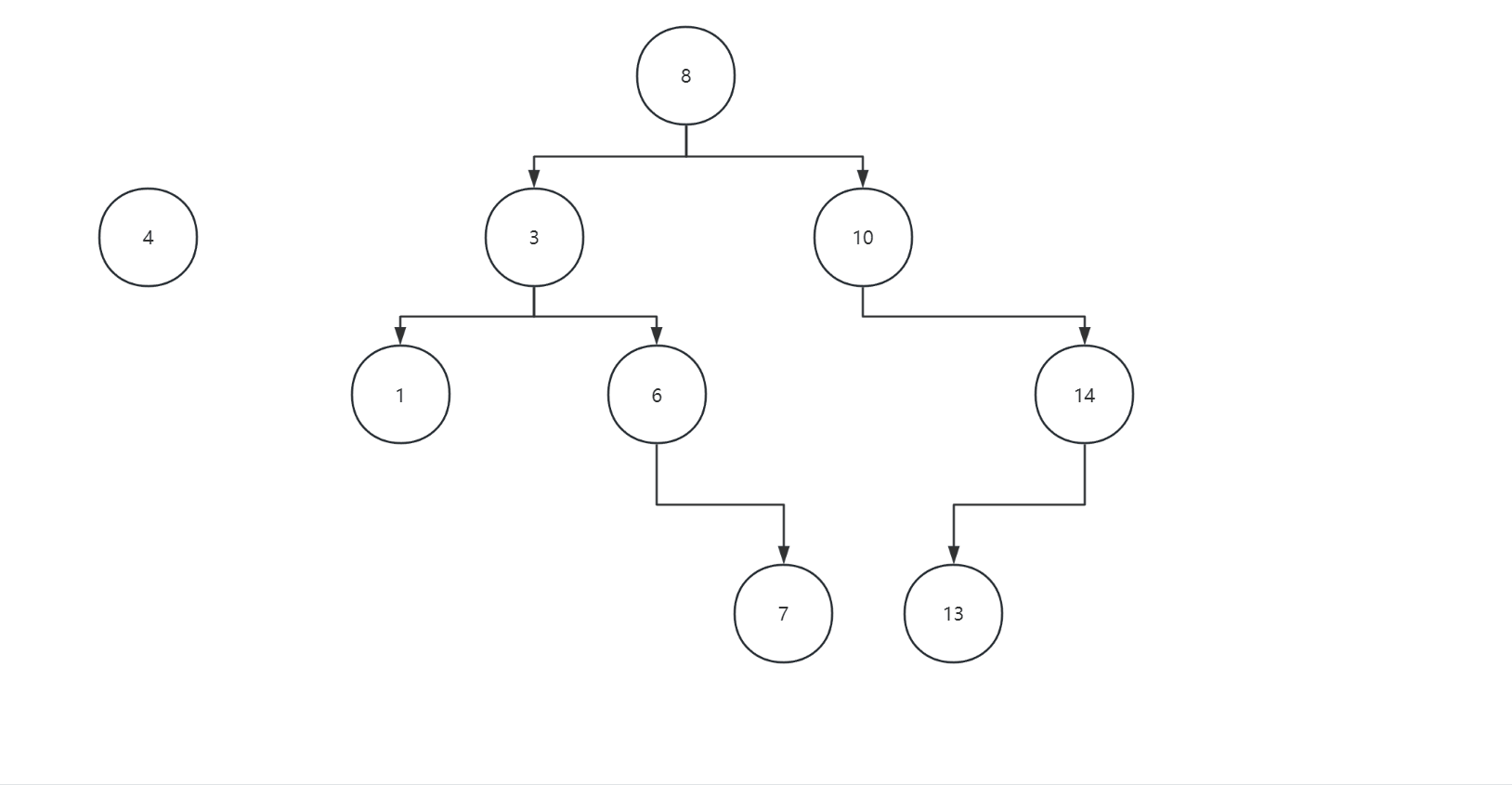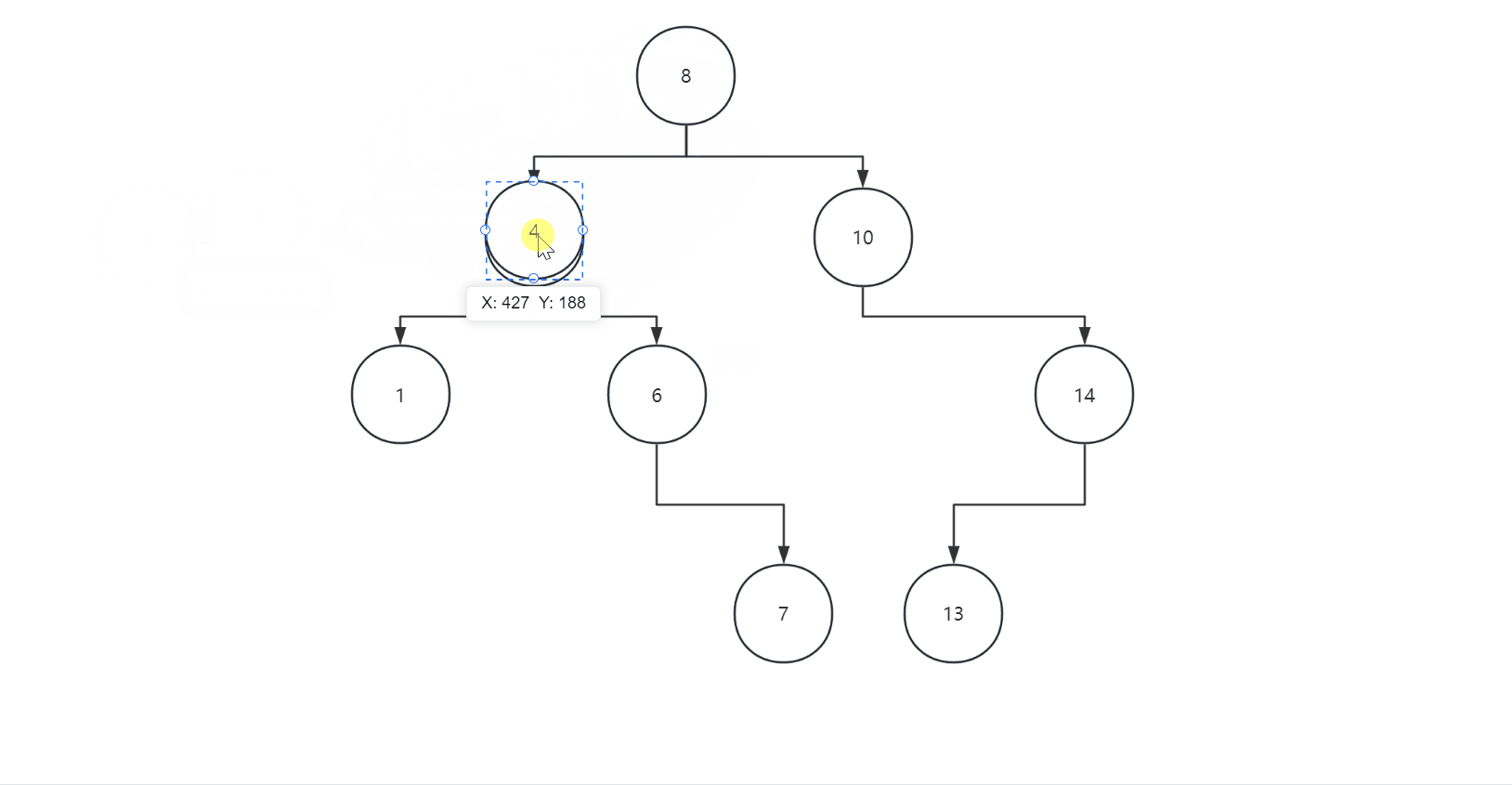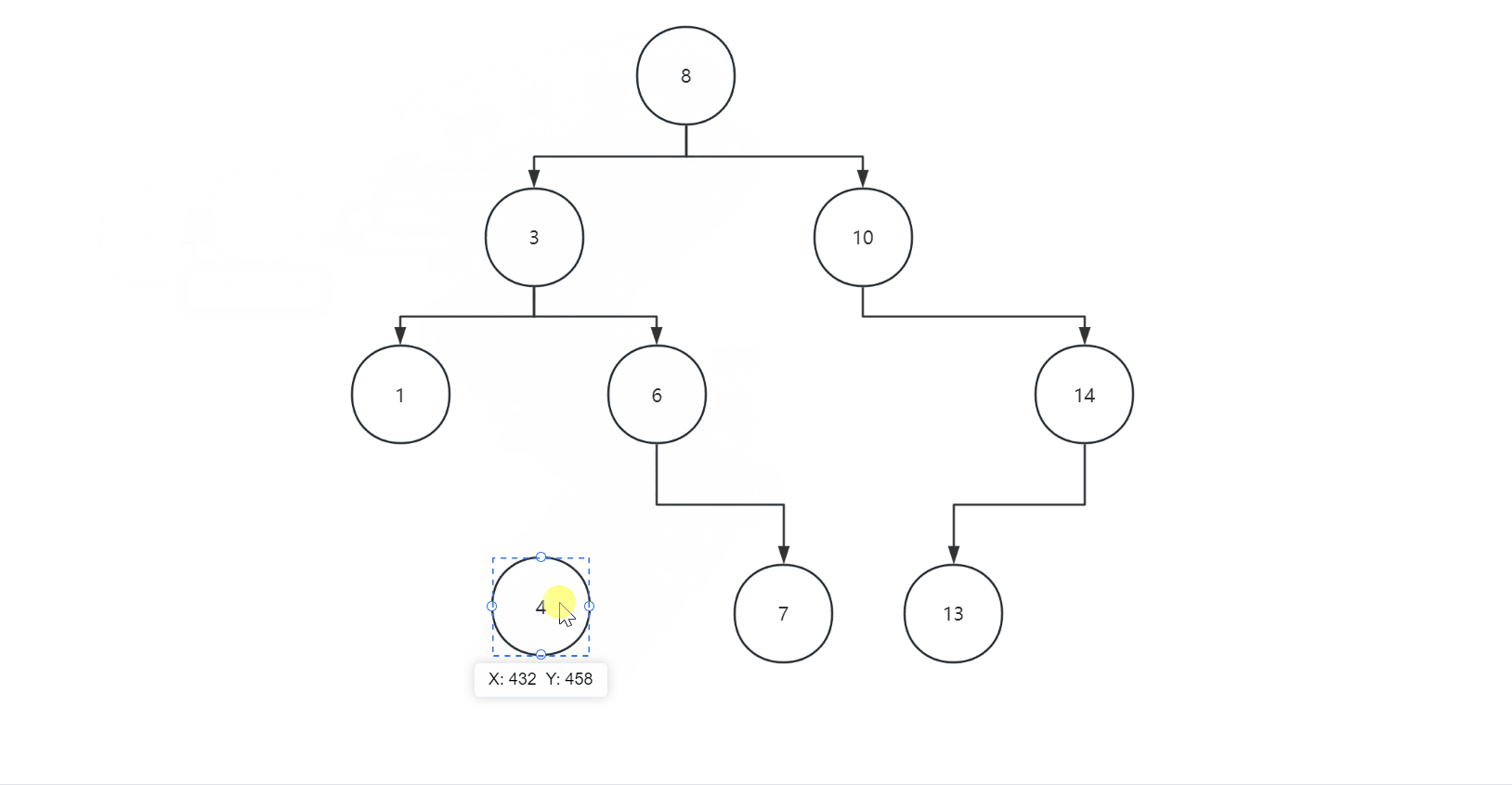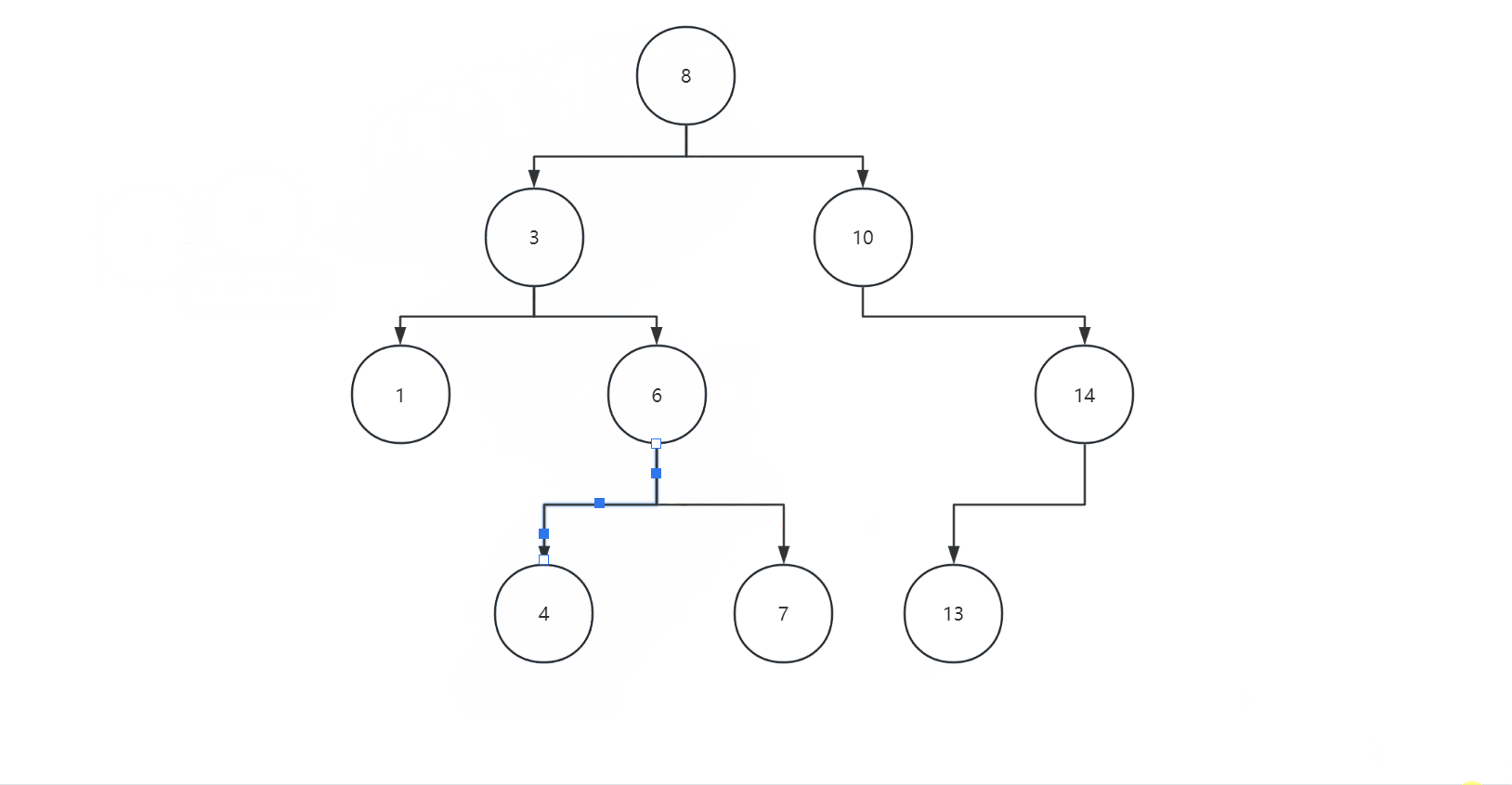
我们的代码如下：
bool insert(const K &key)
{
Node* newnode = new Node(key);
if (_root == nullptr) _root = newnode;
else
{
Node* cur = _root, *parent = nullptr;
while (cur)
{
parent = cur;
if (key < cur->_key) cur = cur->_left;
else if (key > cur->_key) cur = cur->_right;
else return false;
}
if (key < parent->_key) parent->_left = newnode;
else parent->_right = newnode;
}
return true;
}先判断时不是根节点，然后再根据二叉搜索树的规则进行插入。
2.2遍历
我们遍历就是二叉树的中序遍历，这样遍历就是天然有序的从小到大进行排序的数据，我们看代码：
public:
void InOrder()
{
_InOrder(_root);
}
private:
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}这里为什么会选择让函数在private里和public里呢？主要就是我们需要使用_root这个成员变量，我们可以使用缺省 ，但是会报错，我们想要使用成员变量我们就可以将函数封装在privae里面，然后调用就可以了。
2.3查找
二叉搜索树的查找和插入类似，我们查找某一个值就相当于插入某一个值，根据插入规则就可以找到某一个值，我们看下面图片：
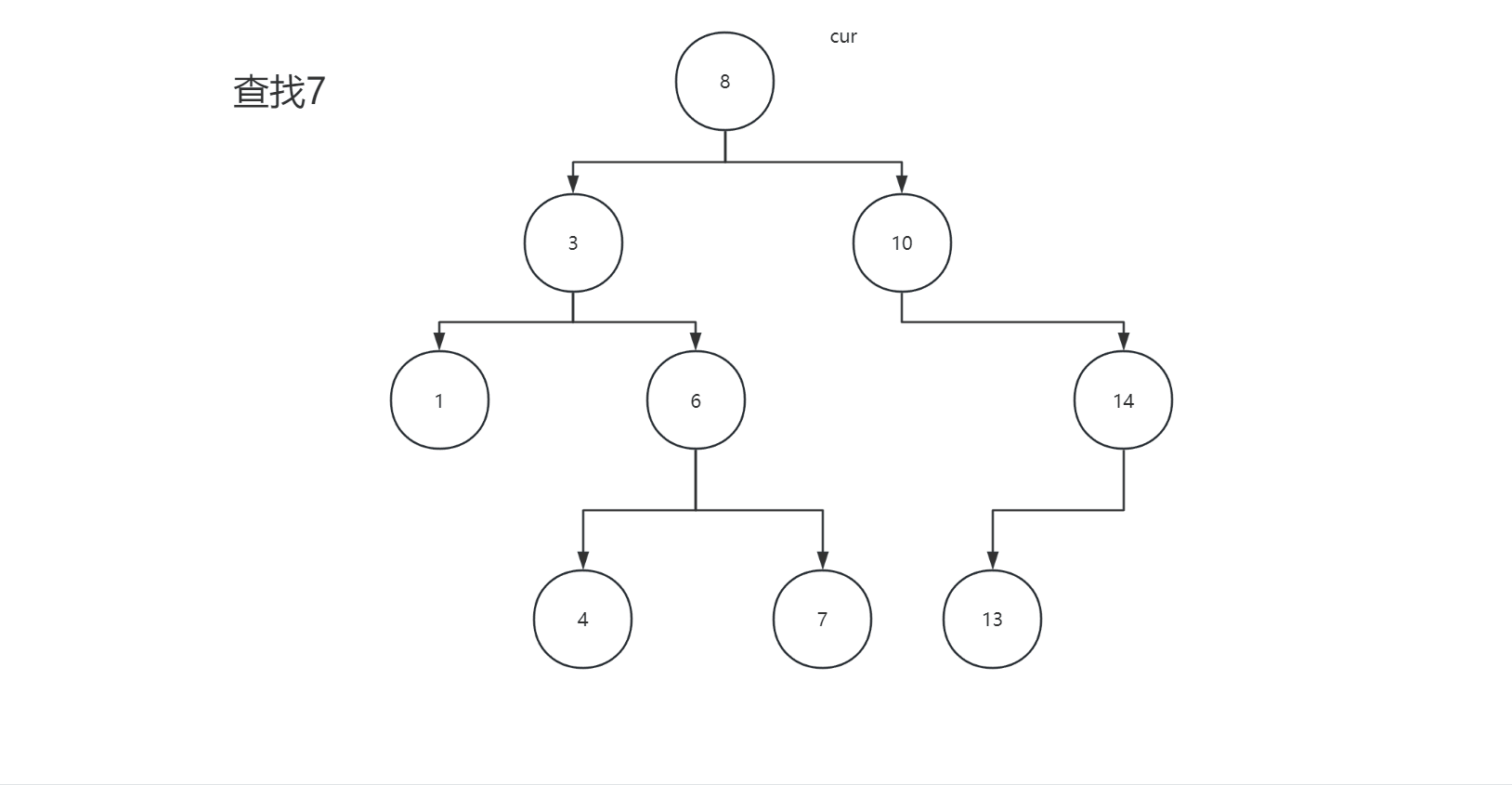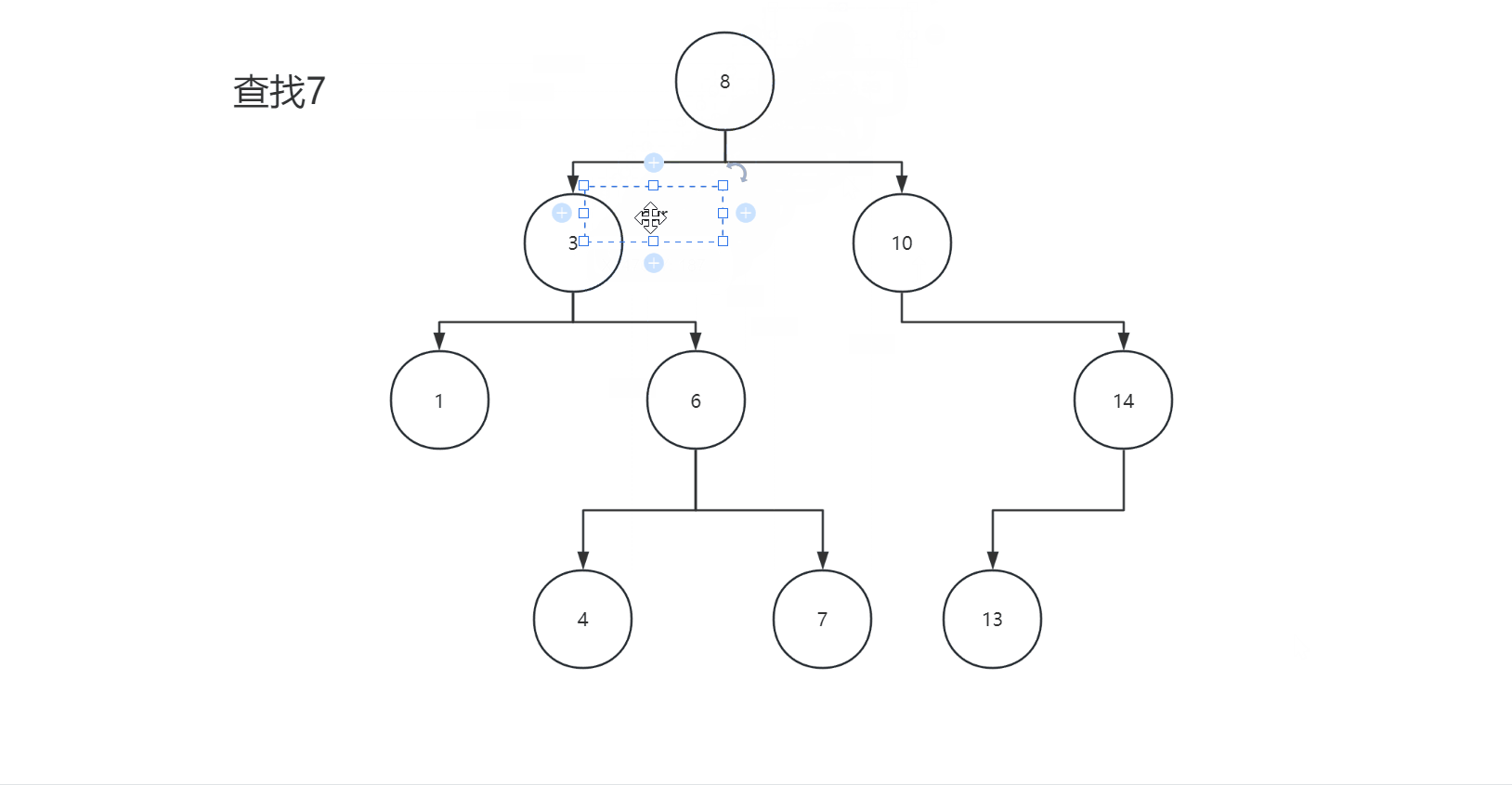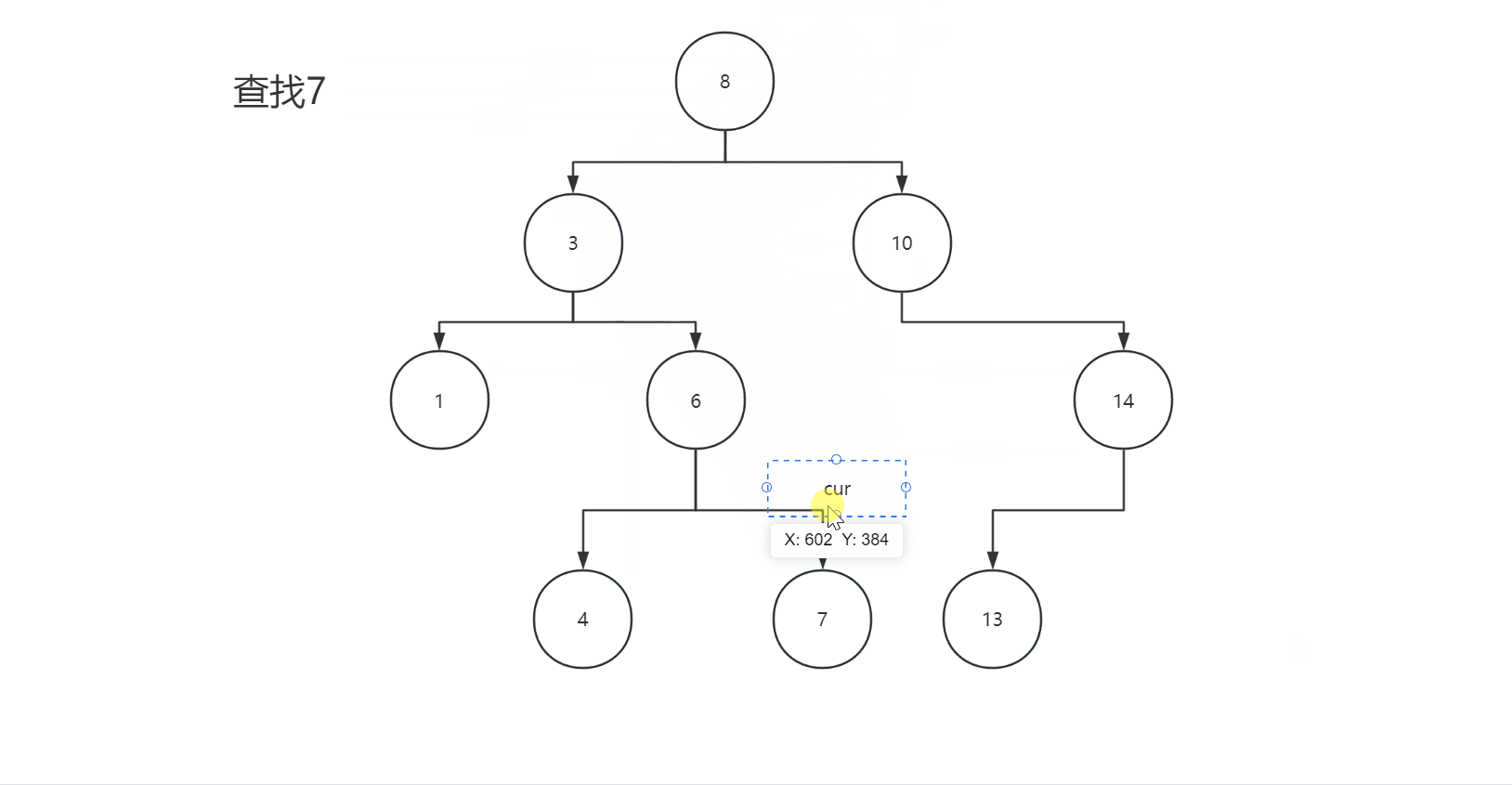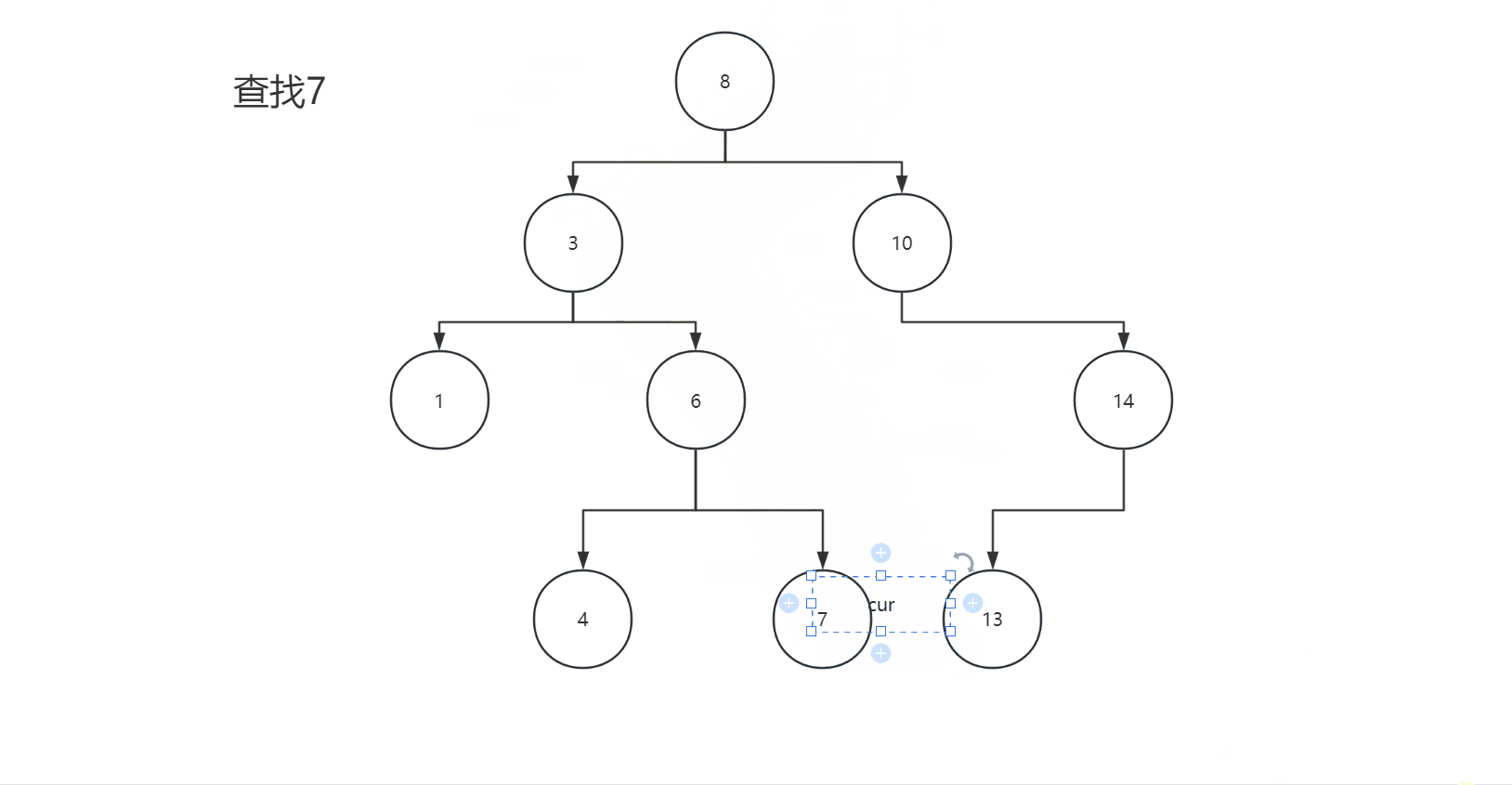
我们看代码：
bool Find(const K &key)
{
Node* cur = _root;
while (cur)
{
if (key < cur->_key) cur = cur->_left;
else if (key > cur->_key) cur = cur->_right;
else return true;
}
return false;
}2.4删除
在这里我们的删除分为：删除节点的左子树为空，删除节点的右子树为空，删除节点的左子树和右子树都不为空这三种情况（删除节点的左子树和右子树都为空在删除节点的左子树为空情况中）。
2.4.1删除节点的左子树为空
分为删除节点为根节点和删除节点不为根节点，我们看下面动图:
2.4.2删除节点的右子树为空
分为删除节点为根节点和删除节点不为根节点，我们看下面动图:
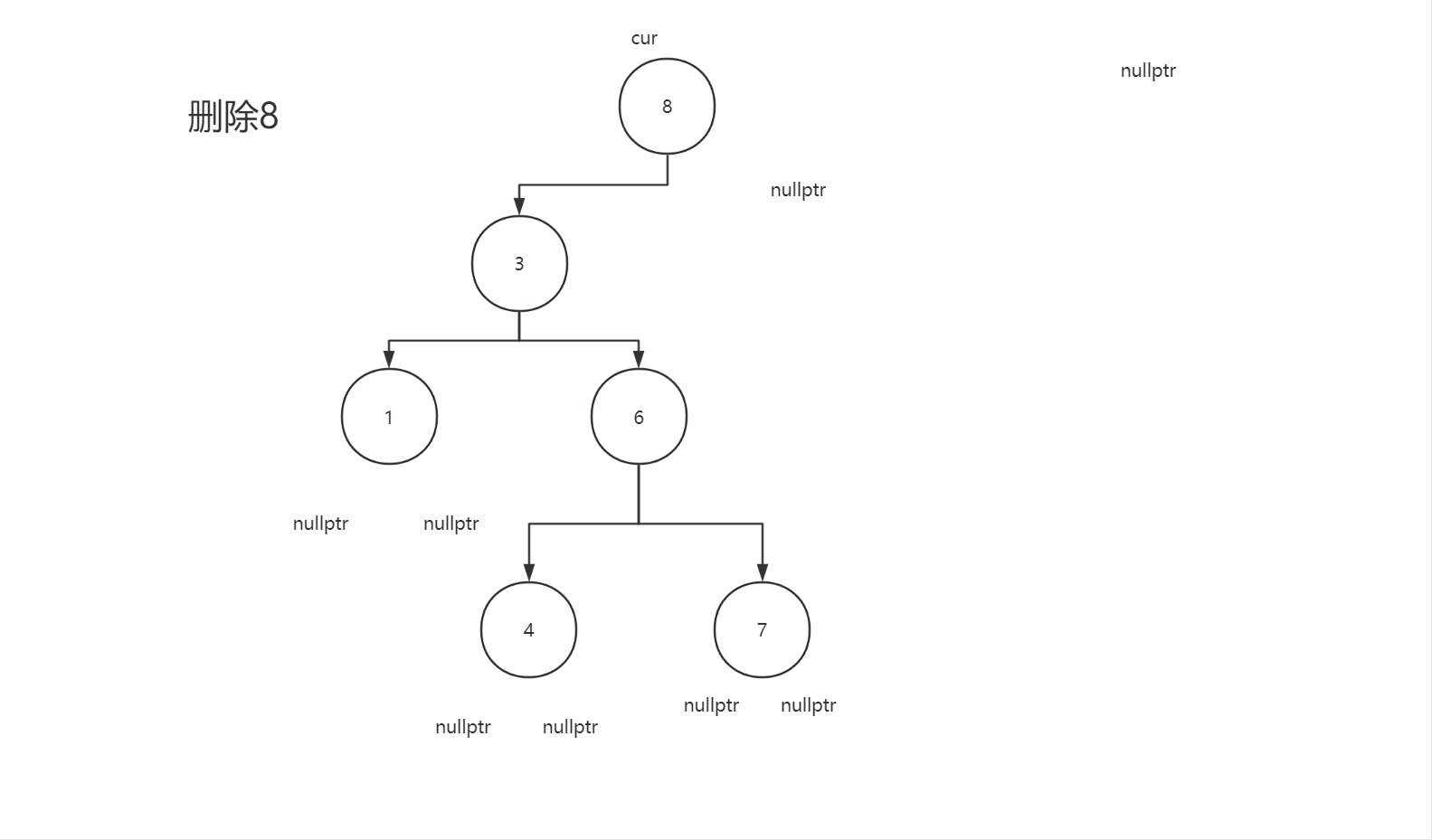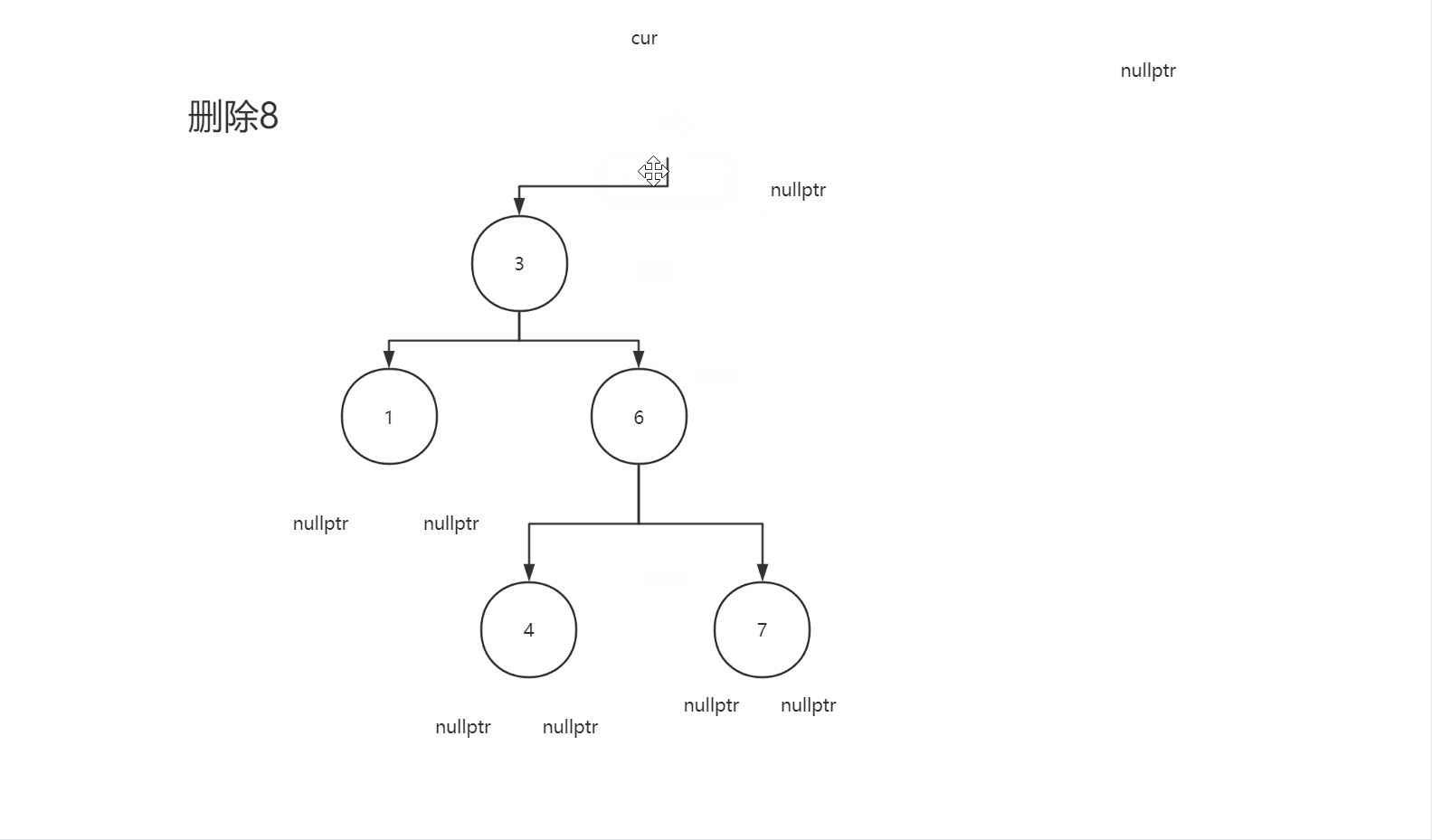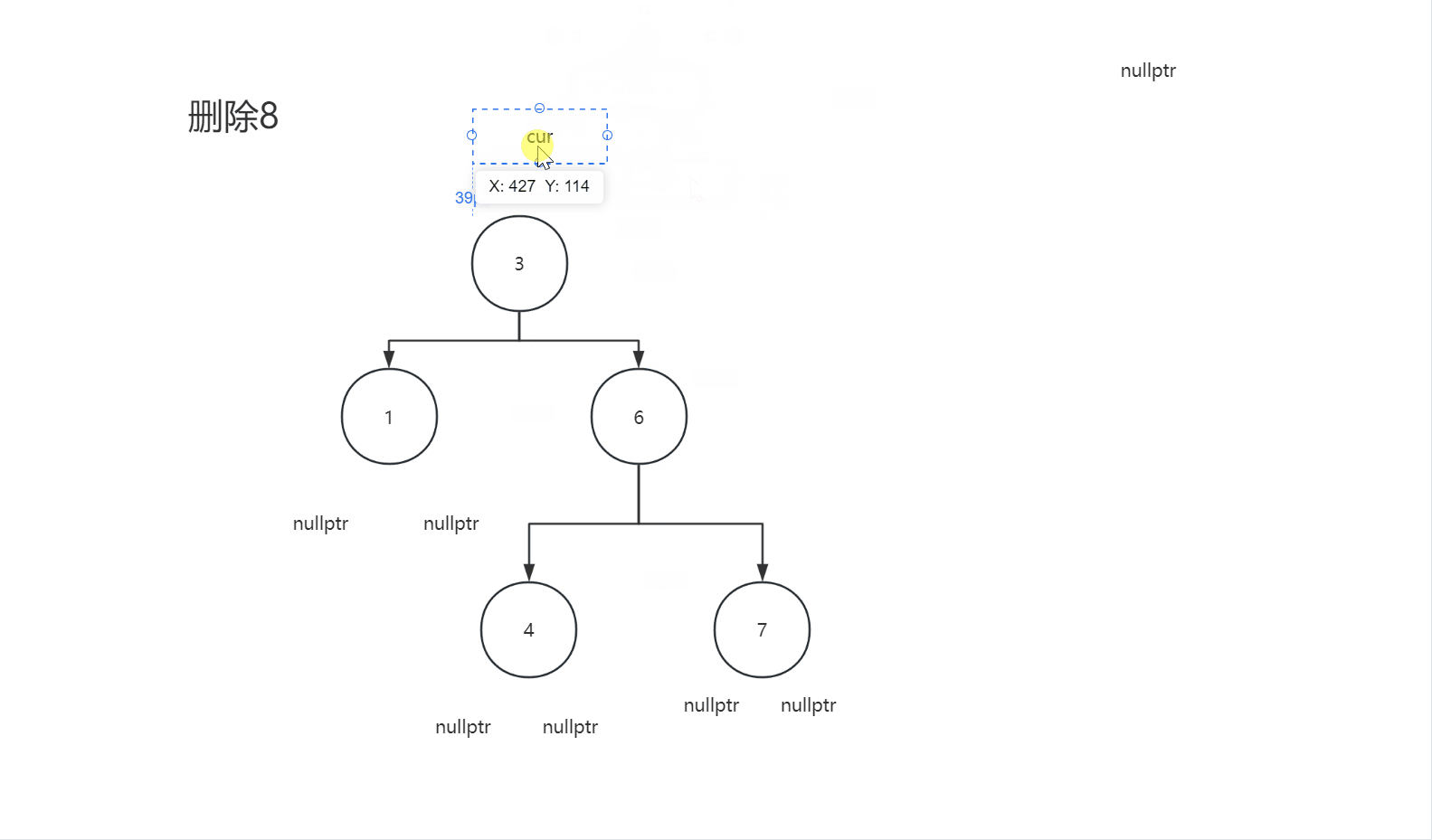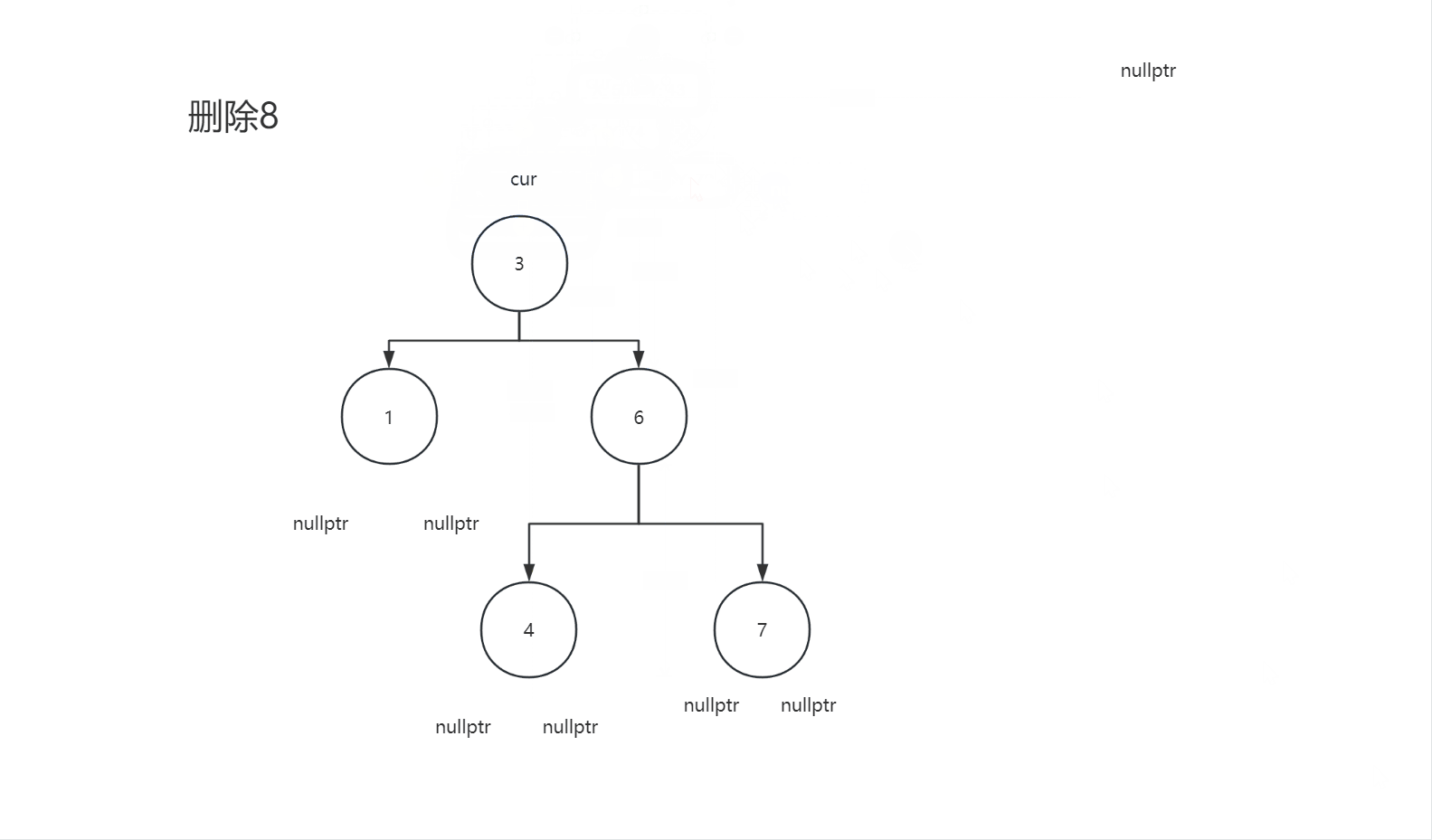
2.4.3删除节点的左子树和右子树都不为空
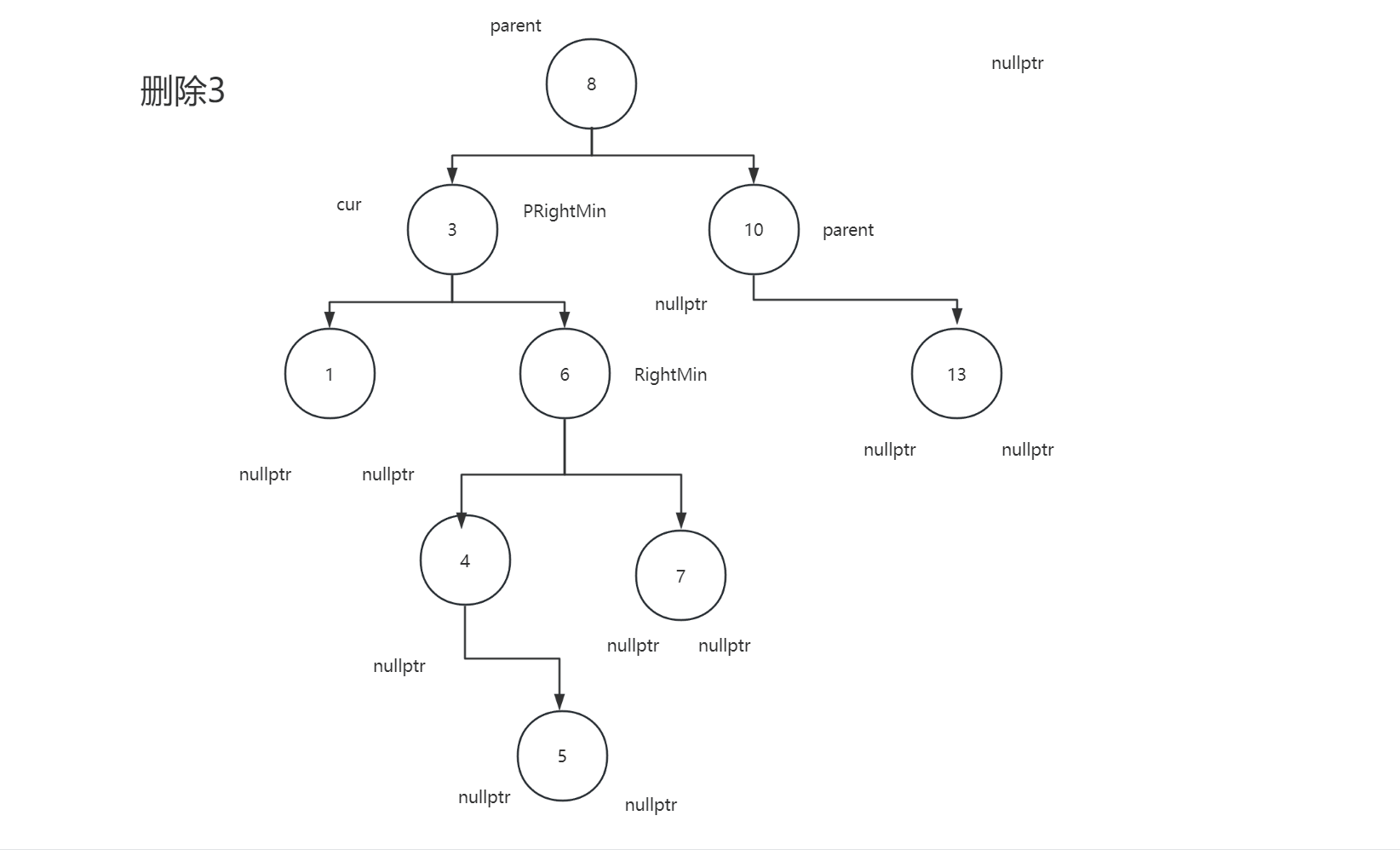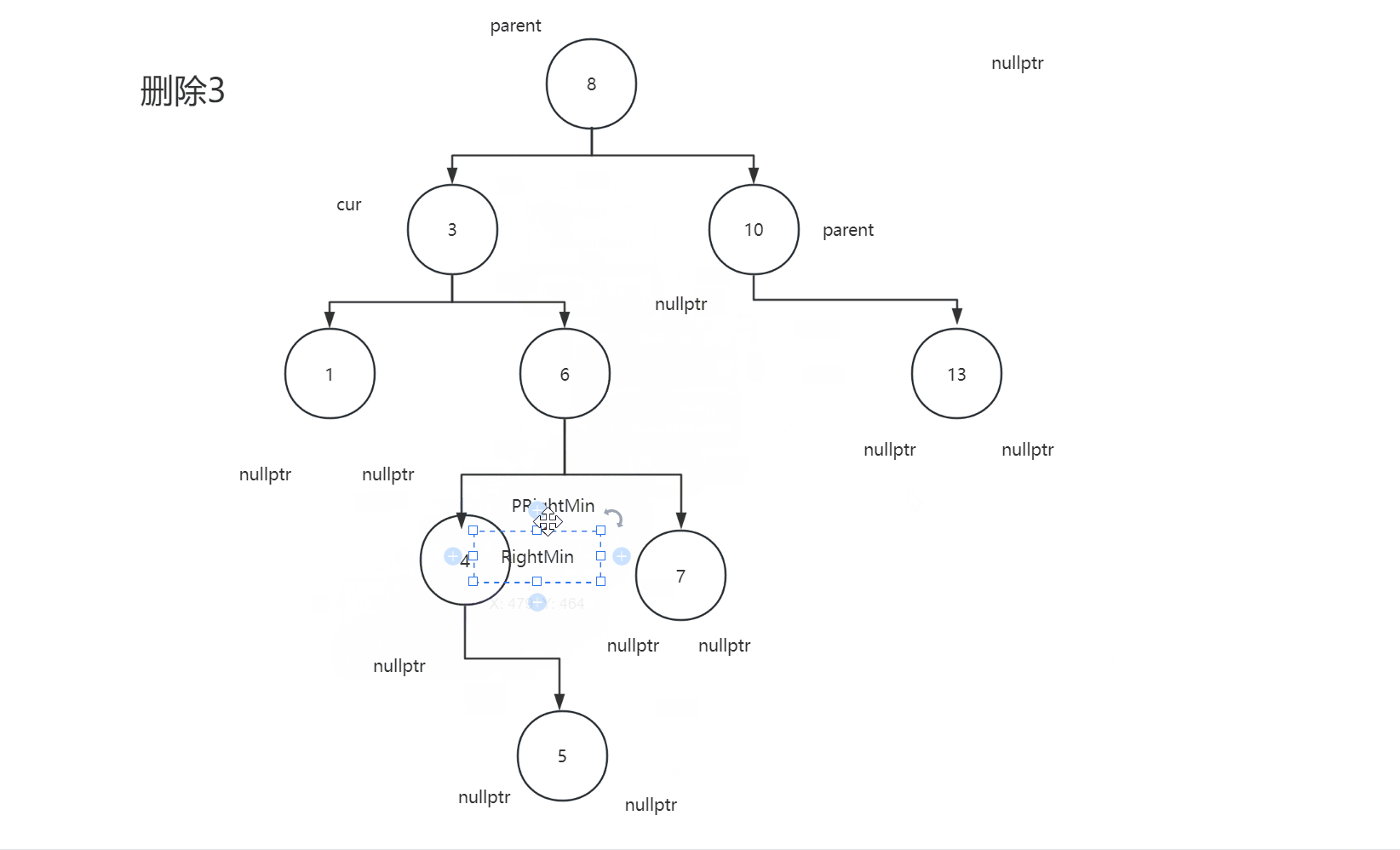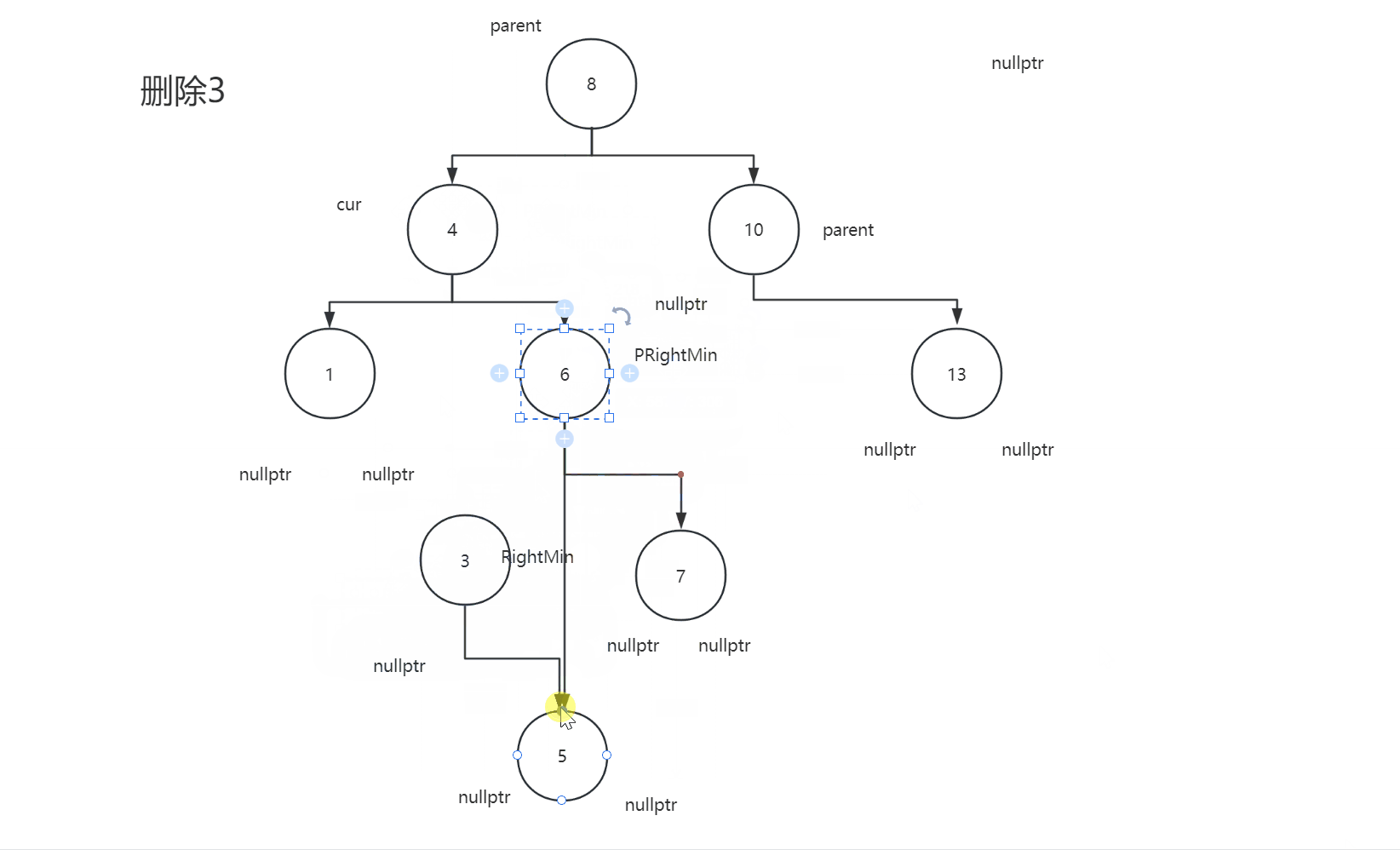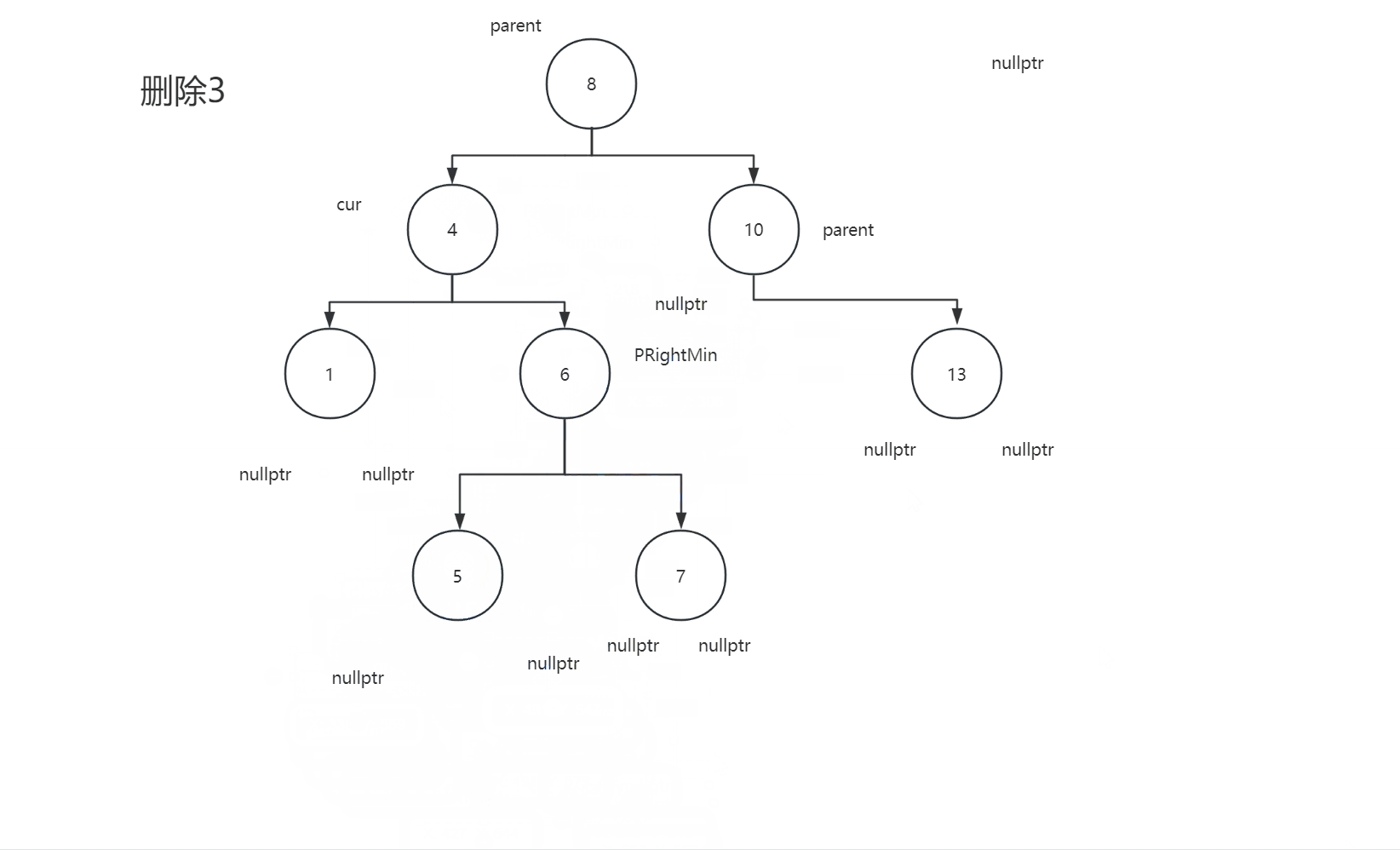2.4.4代码
bool Erase(const K& key)
{
Node* cur = _root, * parent = nullptr;
if (_root == nullptr) return false;
while (cur)
{
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else
{
if (cur->_left == nullptr)
{
if (cur == _root) _root = cur->_right;
else
{
if (parent->_left == cur) parent->_left = cur->_right;
else parent->_right = cur->_right;
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (cur == _root) _root = cur->_left;
else
{
if (parent->_left == cur) parent->_left = cur->_left;
else parent->_right = cur->_left;
}
delete cur;
}
else
{
Node* RightMin = cur->_right;
Node* PRightMin = cur;
while (RightMin->_left )
{
PRightMin = RightMin;
RightMin = RightMin->_left;
}
swap(RightMin->_key, cur->_key);
if(PRightMin->_left ==RightMin) PRightMin->_left = RightMin->_right ;
else PRightMin->_right = RightMin->_right;
delete RightMin;
}
return true;
}
}
return false;
}三.K-V模型
K—V模型和上面的代码类似，只是多一个V值，下面是代码这里不做具体分析
template<class K,class V>
struct BSTreeNode
{
typedef BSTreeNode<K,V> Node;
Node* _left;
Node* _right;
K _key;
V _val;
BSTreeNode(const K& key，const V&val)
:_left(nullptr)
, _right(nullptr)
,_key(key)
, _val(val)
{}
};
template<class K,class V>
class BSTree
{
public:
typedef BSTreeNode<K,V> Node;
//中序遍历
void INOrder()
{
_INOrder(_root);
cout << endl;
}
//插入
bool insert(const K& key , const V&val)
{
Node* newnode = new Node(key,val);
if (_root == nullptr)
{
_root = newnode;
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < val)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > val)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
if (val > parent->_val)
{
parent->_right = newnode;
}
else
{
parent->_left = newnode;
}
return true;
}
//查找
Node* find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
//删除
bool erase(const K& key)
{
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
if (cur->_left == nullptr)
{
if (_root == cur)
{
_root = cur->_right;
}
if (parent->_left == cur) parent->_left = cur->_right;
else parent->_right = cur->_right;
delete cur;
}
else if (cur->_right == nullptr)
{
if (_root == cur)
{
_root = cur->_left;
}
if (parent->_left == cur) parent->_left = cur->_left;
else parent->_right = cur->_left;
delete cur;
}
else
{
//找到左子树的最大值或者右子树的最小值，进行替换
//Node* LessNodeParent = nullptr;
Node* LessNodeParent = cur;
Node* LessNode = cur->_right;
while (LessNode->_left)
{
LessNodeParent = LessNode;
LessNode = LessNode->_left;
}
swap(cur->_key, LessNode->_key);
swap(cur->_val, LessNode->_val);
if (LessNodeParent->_left == LessNode) LessNodeParent->_left = LessNode->_right;
else LessNodeParent->_right = LessNode->_right;
delete LessNode;
}
return true;
}
}
return false;
}
private:
void _INOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_INOrder(root->_left);
cout << root->_val << " ";
_INOrder(root->_right);
}
Node* _root = nullptr;
};
四.二叉搜索树的性能分析
插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数，即结点越深，则比较次数越多。但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：
最优情况下，二叉搜索树为完全二叉树(或者接近完全二叉树)，其平均比较次数为：log_2 N
最差情况下，二叉搜索树退化为单支树(或者类似单支)，其平均比较次数为：N
