033.搜索旋转排序数组

news2024/10/6 20:34:20

题意

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给方法之前，nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标从 0 开始计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你旋转后的数组 nums 和一个整数 target，如果 nums 中存在这个目标值 target，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

难度

中等

示例

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

分析 1

这道题咋眼一看，有点绕，给一个旋转后的数组，和一个目标值，并要求我们找到这个目标值的下标。

但稍微分析一下就知道，就是在一个数组当中查找一个目标值，如果不考虑时间复杂度的话，我们可以直接遍历一遍，找到就返回下标，找不到就返回-1。

超级简单：

class Solution {
    public int search(int[] nums, int target) {
        for(int i = 0;i < nums.length;i++){
            if(nums[i] == target)
                return i;
        }
        return -1;
    }
}

来看一下效率：

效率不错，但要时间复杂度为对数级别。那就要考虑别的算法

分析 2

我们知道，在一个有序的数组里面去判断一个数是否存在，可以利用二分查找，时间复杂度刚好就是$O(\log{n})$。

但这道题只是部分有序（因为旋转了），该怎么去判断呢？

闭上眼，想一下。

从任意位置将这个部分有序的数组分开，那么分开之后的两部分必然有一部分是有序的！

比如：

nums = [4,5,6,7,0,1,2]      
nums = [4] [5,6,7,0,1,2]	breakPos = 1
nums = [4,5] [6,7,0,1,2]    breakPos = 2
nums = [4,5,6] [7,0,1,2]    breakPos = 3
nums = [4,5,6,7] [0,1,2]    breakPos = 4
nums = [4,5,6,7,0] [1,2]    breakPos = 5
nums = [4,5,6,7,0,1] [2]    breakPos = 6

果然，至少有一部分是有序的。那我们是不是就可以从有序的部分当中去寻找 target 呢？

可以是可以，但时间复杂度并不是 $O(\log{n})$，还要加上 breakPos 分割后无序的部分，合起来就是$O(n + \log{n})$，显然也不符合题目的要求。

考虑下面的思路：

如果[lef,breakPos - 1]是有序的，而且nums[lef] <= target && target < nums[breakPos]，那么答案肯定在[lef, breakPos - 1]，直接调整上界rig到breakPos - 1。
如果[breakPos，rig]是有序的，而且nums[breakPos] < target && target <= nums[rig]，那么答案肯定在[breakPos,rig]中，调整下界lef到breakPos即可。

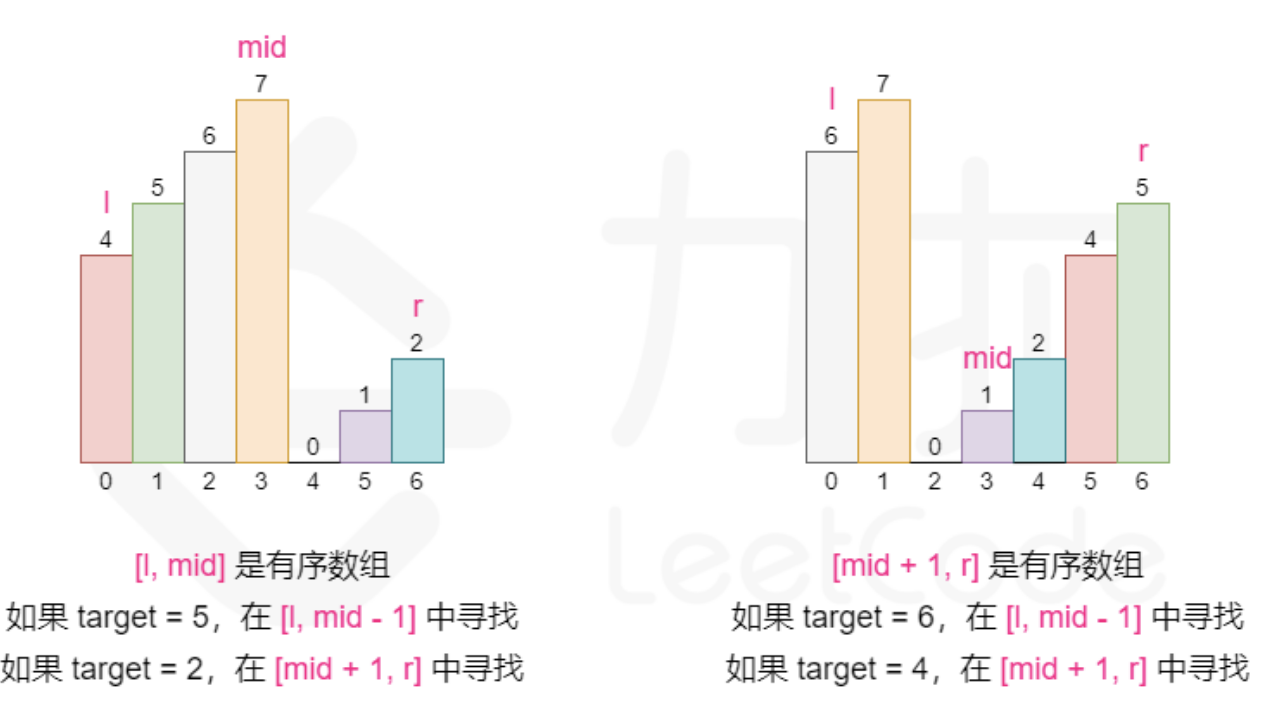
也就是说，我们通过判断有序的部分，来决定下一步的查找范围。

只有在有序区间内才可以通过区间两端的数值判断 target 是否在其中。
判断有序区间还是乱序区间：left <= right 是顺序区间，否则乱序区间。
每次二分至少存在一个有序区间。

class Solution {
    public int search(int[] nums, int target) {
        int siz = nums.length; // 数组长度
        int lef = 0, rig = siz - 1; // 初始化左右指针
        while (lef <= rig) { // 当左指针小于等于右指针时进行循环
            int mid = (lef + rig) >> 1; // 计算中间索引，使用右移运算符相当于除以 2
            if (nums[mid] == target) // 如果中间元素等于目标值，返回中间索引
                return mid;
            if (nums[0] <= nums[mid]) { // 如果左半部分有序
                if (nums[0] <= target && target < nums[mid]) // 如果目标值在左半部分范围内
                    rig = mid - 1; // 移动右指针
                else
                    lef = mid + 1; // 否则移动左指针
            } else { // 右半部分有序
                if (nums[mid] < target && target <= nums[siz - 1]) //如果目标值在右半部分范围内
                    lef = mid + 1; // 移动左指针
                else
                    rig = mid - 1; // 否则移动右指针
            }
        }
        return -1; // 如果未找到目标值，返回 -1
    }
}