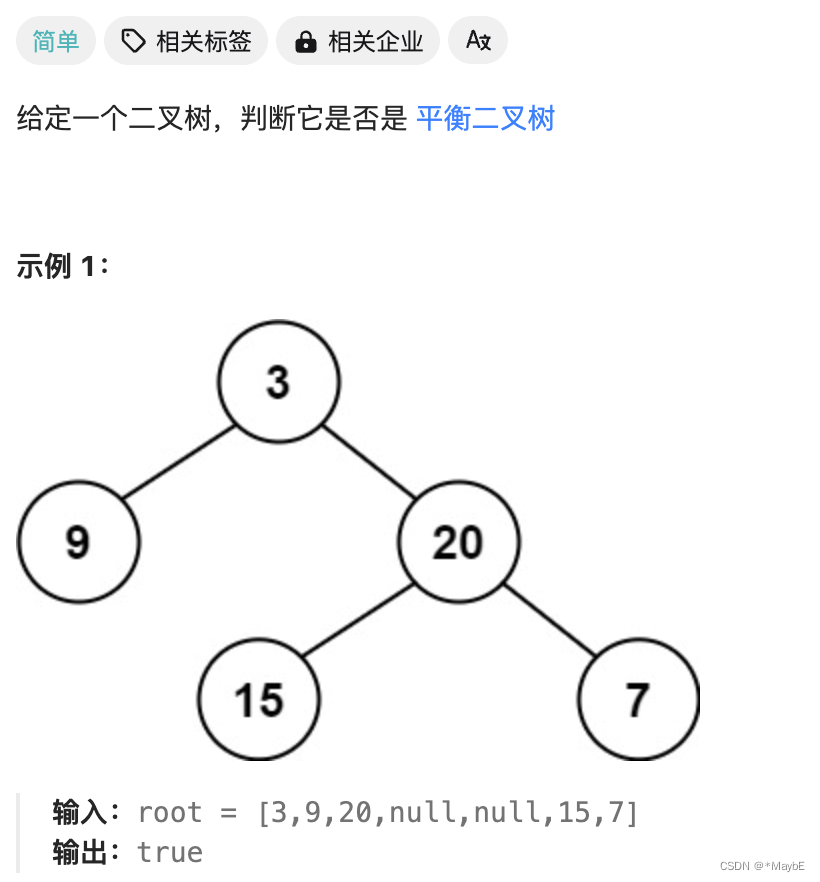
110.平衡二叉树

题目链接：110.平衡二叉树
文档讲讲：代码随想录
状态：还可以

思路：计算左右子树的深度差，递归判断左右子树是否符合平衡条件

题解：

    public boolean isBalanced(TreeNode root) {
        if (root == null) {
            return true;
        }
        int leftLen = getMaxLen(root.left);
        int rightLen = getMaxLen(root.right);

        return Math.abs(leftLen - rightLen) <= 1 && isBalanced(root.left) && isBalanced(root.right);
    }

    public int getMaxLen(TreeNode node) {
        if (node == null) {
            return 0;
        }
        int leftLen = getMaxLen(node.left);
        int rightLen = getMaxLen(node.right);
        return Math.max(leftLen, rightLen) + 1;
    }

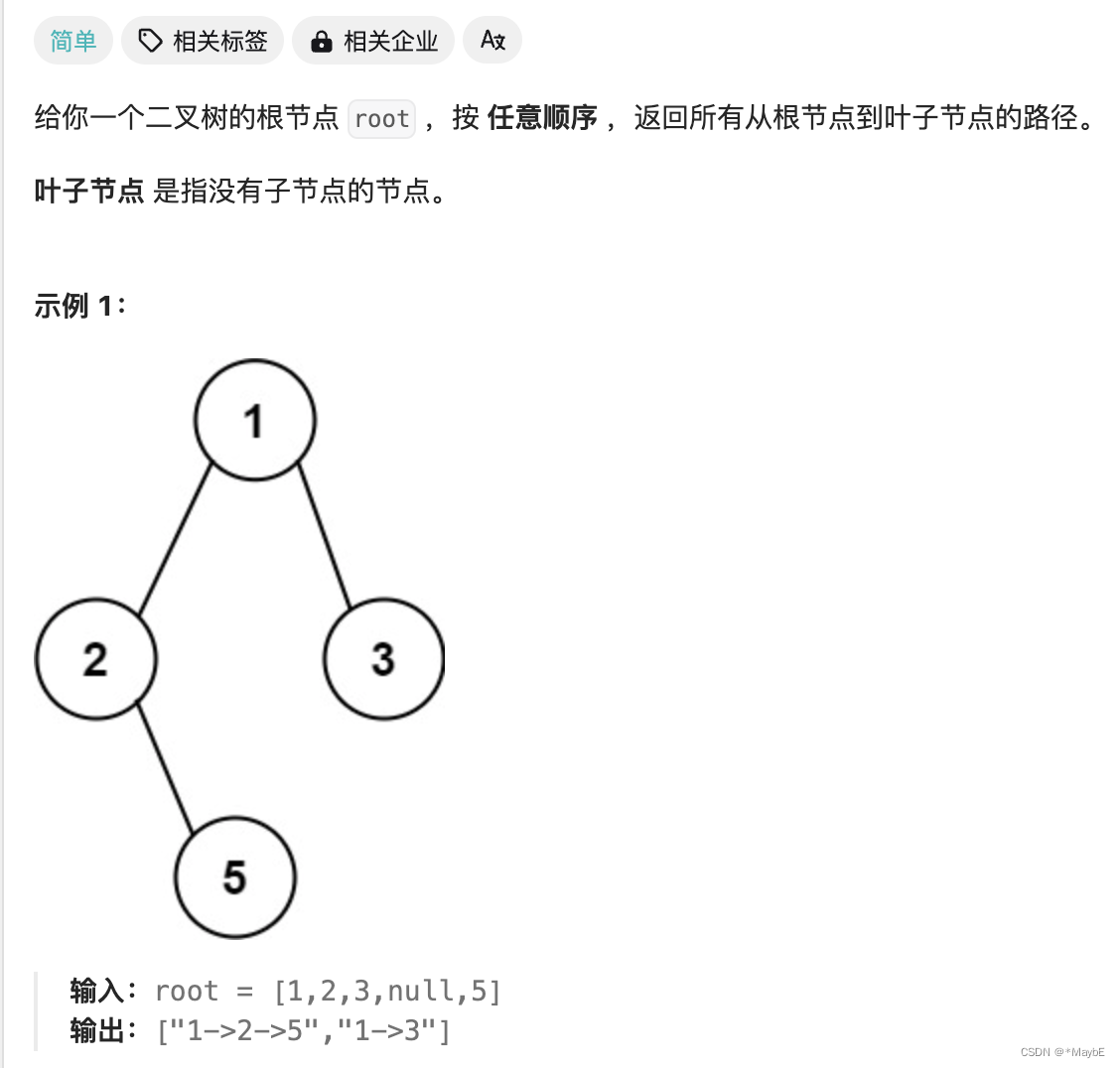
257. 二叉树的所有路径

题目链接： 257. 二叉树的所有路径
文档讲解：代码随想录
状态：没写出来

思路：前序+回溯的思路，遇到叶子节点收集路径

递归解法：

    public List<String> binaryTreePaths(TreeNode root) {
        List<String> res = new LinkedList<>();
        StringBuilder sb = new StringBuilder();
        getPath(root, res, sb);
        return res;
    }

    public void getPath(TreeNode root, List<String> res, StringBuilder sb) {
        if (root == null) {
            return;
        }
        int length = sb.length();
        sb.append(root.val);
        if (root.left == null && root.right == null) {
            res.add(sb.toString());
        } else {
            sb.append("->");
            getPath(root.left, res, sb);
            getPath(root.right, res, sb);
        }
        sb.setLength(length); // 恢复StringBuilder的状态
    }

迭代解法：

    public List<String> binaryTreePaths(TreeNode root) {
        List<String> res = new LinkedList<>();
        if (root == null) {
            return res;
        }

        // 创建双端队列来存储节点和路径
        Deque<TreeNode> deque = new LinkedList<>();
        Deque<String> pathDeque = new LinkedList<>();

        // 初始节点和路径
        deque.addLast(root);
        pathDeque.addLast(Integer.toString(root.val));

        while (!deque.isEmpty()) {
            TreeNode node = deque.pollLast();
            String path = pathDeque.pollLast();
            // 如果当前节点是叶子节点，将路径添加到结果中
            if (node.left == null && node.right == null) {
                res.add(path);
            }
            // 如果右子节点不为空，添加到队列中并更新路径
            if (node.right != null) {
                deque.addLast(node.right);
                pathDeque.addLast(path + "->" + node.right.val);
            }
            // 如果左子节点不为空，添加到队列中并更新路径
            if (node.left != null) {
                deque.addLast(node.left);
                pathDeque.addLast(path + "->" + node.left.val);
            }
        }

        return res;
    }

404.左叶子之和

题目链接： 404.左叶子之和
文档讲解：代码随想录
状态：总觉得自己递归的思路对的，但是结果就是不对，原来是代码中笔误把root.left.right写成了root.right.right。。。。

递归题解：

    public int sumOfLeftLeaves(TreeNode root) {
        // 如果根节点为空，返回0
        if (root == null) {
            return 0;
        }

        // 检查当前节点的左子节点是否为叶子节点
        if (root.left != null && root.left.left == null && root.left.right == null) {
            // 如果左子节点是叶子节点，返回左叶子节点的值，加上左子树和右子树的左叶子节点值
            return root.left.val + sumOfLeftLeaves(root.left) + sumOfLeftLeaves(root.right);
        } else {
            // 如果左子节点不是叶子节点，递归遍历左子树和右子树
            return sumOfLeftLeaves(root.left) + sumOfLeftLeaves(root.right);
        }
    }

迭代题解：

    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int sum = 0;
        Deque<TreeNode> deque = new LinkedList<>();
        deque.addLast(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            while (size-- > 0) {
                TreeNode node = deque.pollFirst();
                if (node.left != null) {
                    if (node.left.left == null && node.left.right == null) {
                        sum += node.left.val;
                    }
                    deque.addLast(node.left);
                }
                if (node.right != null) {
                    deque.addLast(node.right);
                }
            }
        }
        return sum;
    }