分发饼干

455. 分发饼干 - 力扣（LeetCode）

贪心算法，让每个饼干给到能够满足的孩子，所以需要对饼干尺寸和孩子的满足值先进行排序，然后针对每一个饼干的尺寸，挑选恰好能够满足的孩子（这里表述可能不准确，即从大到小，都选择能够满足的孩子，满足后结果返回值加1），这里选用while循环比较简单，具体代码如下。

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        // 对孩子的胃口值和饼干的尺寸进行排序
        sort(g.begin(),g.end());
        sort(s.begin(),s.end());
        // 初始化饼干索引为饼干数组的最后一个元素
        int index = s.size()-1;
        int result = 0;
        // 从孩子的胃口值数组的最后一个元素开始遍历
        int i = g.size()-1;
        // 当饼干索引大于等于0时，继续执行
        while(index>=0){
            // 如果孩子的索引小于0，则所有孩子都已被考虑，跳出循环
            if(i < 0){
                break;
            }
            // 如果当前饼干可以满足当前孩子（饼干的尺寸大于等于孩子的胃口值）
            if(s[index]>=g[i]){
                // 移动到下一个孩子和下一个饼干
                index--;
                i--;
                // 结果加一
                result++;
            }
            else{
                // 如果当前饼干不能满足当前孩子，则移动到下一个孩子
                i--;
            }
        }
        // 返回可以满足的孩子数量
        return result;
    }
};

算法的时间复杂度为O(nlogn)，排序需要O(nlogn)，循环遍历一次需要O(n)，总体需要O(nlogn)的复杂度，空间复杂度考虑排序需要的空间O(logn),其余所需的空间为O(1)，所以空间复杂度应该为O(logn)。

摆动序列

376. 摆动序列 - 力扣（LeetCode）

具体参考代码随想录，确实没想到。。。

代码随想录 (programmercarl.com)https://programmercarl.com/0376.%E6%91%86%E5%8A%A8%E5%BA%8F%E5%88%97.html#%E6%80%9D%E8%B7%AF

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        if (nums.size() <= 1) return nums.size();
        int curDiff = 0; // 当前一对差值
        int preDiff = 0; // 前一对差值
        int result = 1;  // 记录峰值个数，序列默认序列最右边有一个峰值
        for (int i = 0; i < nums.size() - 1; i++) {
            curDiff = nums[i + 1] - nums[i];
            // 出现峰值
            if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
                result++;
                preDiff = curDiff; // 注意这里，只在摆动变化的时候更新prediff
            }
        }
        return result;
    }
};

算法时间复杂度为O(n)遍历一次，空间复杂度为O(1)。

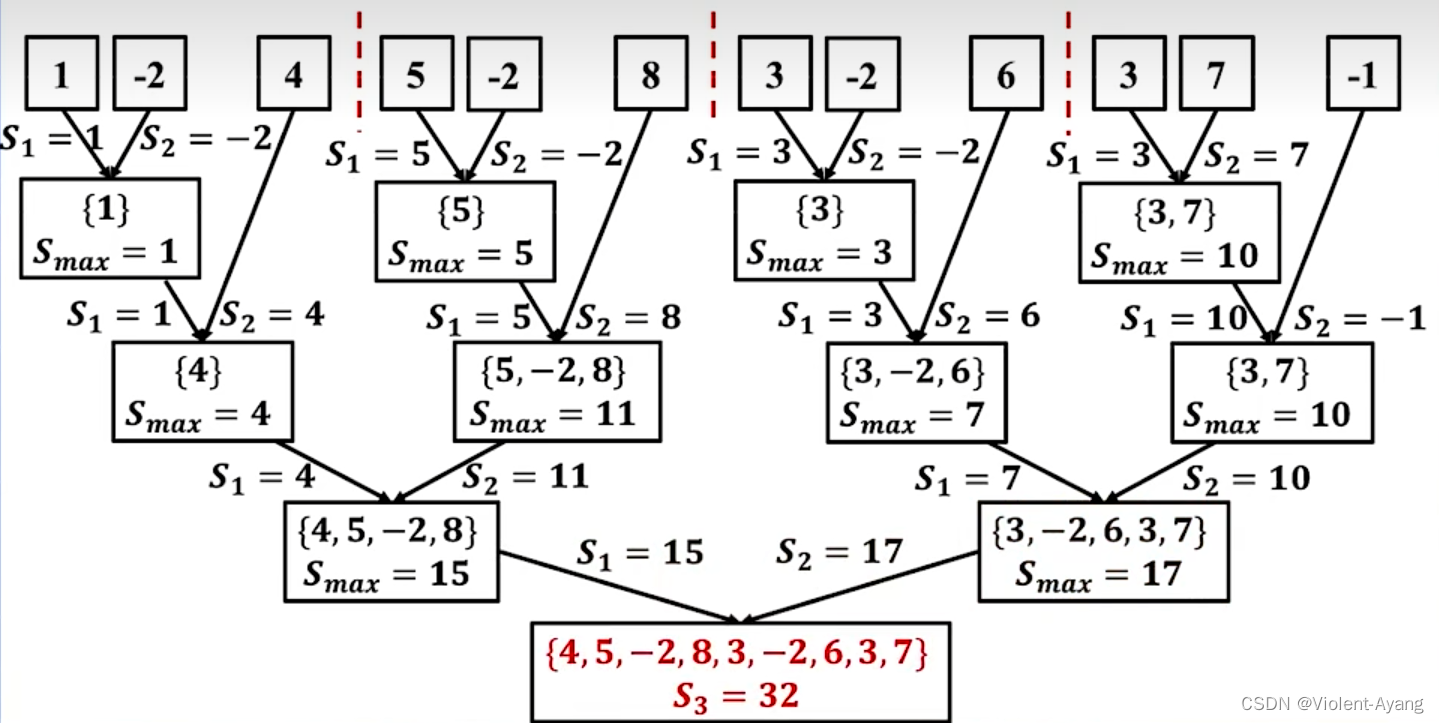
最大子序和

53. 最大子数组和 - 力扣（LeetCode）

如果在某个点，当前子数组的和变成了负数，那么它对于后续的子数组来说就没有任何益处，因此，可将其重置为0，同时，每次都记录下当前子数组和的最大值，这样就可以找到全局的最大子数组和。

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        // 初始化当前子数组的和为0
        int sum = 0;
        // 初始化最大子数组和为数组的第一个元素
        int pre = nums[0];
        // 遍历数组中的每个元素
        for(int i = 0; i < nums.size();i++){
            // 将当前元素加到当前子数组的和上
            sum += nums[i];
            // 如果当前子数组的和大于之前记录的最大子数组和，则更新最大子数组和
            if(sum>pre){
                pre = sum;
            }
            // 如果当前子数组的和小于0，则重置当前子数组和为0
            // 这是因为负数会减少子数组的和，所以不可能成为最大子数组和的一部分
            if(sum < 0){
                sum = 0;
            }
        }
        // 返回最大子数组和
        return pre;
    }
};

算法的时间复杂度为O(n)，空间复杂度为O(1)。

感觉贪心算法真的就是能想到的话很简单，想不到的话直接寄啊。。。