概念
分治算法(Divide and Conquer)是一种解决问题的策略,它将一个问题分解成若干个规模较小的相同问题,然后递归地解决这些子问题,最后合并子问题的解得到原问题的解。分治算法的基本思想是将复杂问题分解成若干个较简单的子问题,然后逐个解决这些子问题,最后将子问题的解合并得到原问题的解。
分治算法的基本步骤如下:
-
分解(Divide):将原问题分解成若干个规模较小的相同问题。这些子问题应该是相互独立的,即解决一个子问题不会影响其他子问题的解。
-
解决(Conquer):递归地解决这些子问题。如果子问题的规模足够小,可以直接求解。否则,继续分解子问题,直到子问题可以直接求解。
-
合并(Combine):将子问题的解合并得到原问题的解。这个过程可能涉及到一些计算,但通常比直接解决原问题所需的计算量要少。
分治算法的优点:
- 解决问题的原则是将大问题分解成小问题,降低了问题的复杂度。
- 利用递归的方式解决问题,使得算法具有很好的可读性和可维护性。
- 通过合并子问题的解,可以避免重复计算,提高算法的效率。
分治算法的缺点:
- 分治算法的效率往往受限于递归的深度和每层递归的开销。在某些情况下,分治算法的效率可能不如其他算法。
- 分治算法的递归调用可能导致栈空间的消耗较大,尤其是在递归深度较大的情况下。
分治算法在计算机科学中应用广泛,例如:
- 快速排序、归并排序:这两种排序算法都采用了分治策略,将待排序的序列分成两部分,分别进行排序,然后将排序后的两部分合并成一个有序序列。
- 大整数乘法:分治算法可以用于加速大整数的乘法运算,例如Karatsuba算法。
- 欧几里得算法:用于求解两个整数的最大公约数,采用分治策略,将较大数分解为若干个较小的数,然后递归地求解这些数的最大公约数,最后合并得到原问题的解。
- 循环卷积:分治算法可以用于加速卷积运算,例如快速傅里叶变换(FFT)算法。
总之,分治算法是一种强大的解决问题的策略,通过将复杂问题分解成若干个较简单的子问题,可以降低问题的复杂度,提高算法的效率。
下面本文将介绍几种常见的分治算法应用。
归并排序
【模板】排序
题目描述
将读入的 N N N 个数从小到大排序后输出。
输入格式
第一行为一个正整数 N N N。
第二行包含 N N N 个空格隔开的正整数 a i a_i ai,为你需要进行排序的数。
输出格式
将给定的 N N N 个数从小到大输出,数之间空格隔开,行末换行且无空格。
样例 #1
样例输入 #1
5
4 2 4 5 1
样例输出 #1
1 2 4 4 5
提示
对于 20 % 20\% 20% 的数据,有 1 ≤ N ≤ 1 0 3 1 \leq N \leq 10^3 1≤N≤103;
对于 100 % 100\% 100% 的数据,有 1 ≤ N ≤ 1 0 5 1 \leq N \leq 10^5 1≤N≤105, 1 ≤ a i ≤ 1 0 9 1 \le a_i \le 10^9 1≤ai≤109。
分治算法(Divide and Conquer)
分治算法是一种算法设计范式,它通过将问题分解成多个小问题来解决,然后递归地解决这些小问题,最后将这些小问题的解合并起来得到原问题的解。分治算法通常包括三个步骤:
- 分解(Divide):将原问题分解成若干个规模较小但形式相同的子问题。
- 解决(Conquer):递归地解决这些子问题。如果子问题的规模足够小,则直接解决。
- 合并(Combine):将子问题的解合并,以形成原问题的解。
归并排序的分治策略
归并排序是分治算法的一个经典例子。以下是归并排序的分治过程:
-
分解:将数组分成两半。这是通过找到数组的中间位置来实现的。
-
解决:递归地对这两半进行归并排序。这个过程会一直递归进行,直到每个子数组只有一个元素,这时子数组自然就是有序的。
-
合并:将排序好的两半合并成一个有序的数组。这是通过比较两个子数组的前端元素,并将较小的元素放入结果数组中,直到所有元素都被合并。

图解归并排序
根据图片,我们可以看到归并排序的递归分解过程:
- 最初的数组是 ( [8, 4, 5, 7, 1, 3, 6, 1, 2] )。
- 归并排序首先将数组分解为两半:( [8, 4, 5] ) 和 ( [7, 1, 3, 6, 1, 2] )。
- 然后,每一半再次分解,直到每个子数组只有一个元素。
- 接着,递归地合并这些子数组,直到最终得到一个完全排序的数组。
时间复杂度
归并排序的时间复杂度是 ( O(n \log n) ),其中 ( n ) 是数组的长度。这是因为:
- 分解:分解一个大小为 ( n ) 的数组需要 ( O(\log n) ) 层。
- 合并:每一层的合并操作需要 ( O(n) ) 的时间,因为需要遍历整个数组来合并两个子数组。
- 因此,总的时间复杂度是每层的 ( O(n) ) 乘以层数 ( O(\log n) ),得到 ( O(n \log n) )。
代码如下所示:
#include<bits/stdc++.h>
using namespace std;
int merged[10000],n,a[10001];
void merge(int l1,int r1,int l2,int r2){
int i = l1,j = l2,cnt = 0;
while(i <= r1 && j <= r2){
if(a[i] < a[j]){
merged[cnt++] = a[i++];
}else{
merged[cnt++] = a[j++];
}
}
while(i <= r1){
merged[cnt++] = a[i++];
}
while(j <= r2){
merged[cnt++] = a[j++];
}
for(int t = 0;t < cnt;t ++) a[l1 + t] = merged[t];
}
void merge_sort(int l,int r){
if(l < r){
int mid = (l+r)/2;
merge_sort(l,mid);
merge_sort(mid+1,r);
merge(l,mid,mid+1,r);
}
}
int main(){
cin >> n;
for(int i = 0;i < n;i ++) cin >> a[i];
merge_sort(0,n-1);
for(int i = 0;i < n;i ++){
cout << a[i];
if(i != n-1) cout << " ";
}
}
最大子段和
题目描述
给出一个长度为 n n n 的序列 a a a,选出其中连续且非空的一段使得这段和最大。
输入格式
第一行是一个整数,表示序列的长度 n n n。
第二行有 n n n 个整数,第 i i i 个整数表示序列的第 i i i 个数字 a i a_i ai。
输出格式
输出一行一个整数表示答案。
样例 #1
样例输入 #1
7
2 -4 3 -1 2 -4 3
样例输出 #1
4
提示
样例 1 解释
选取 [ 3 , 5 ] [3, 5] [3,5] 子段 { 3 , − 1 , 2 } \{3, -1, 2\} {3,−1,2},其和为 4 4 4。
数据规模与约定
- 对于 40 % 40\% 40% 的数据,保证 n ≤ 2 × 1 0 3 n \leq 2 \times 10^3 n≤2×103。
- 对于 100 % 100\% 100% 的数据,保证 1 ≤ n ≤ 2 × 1 0 5 1 \leq n \leq 2 \times 10^5 1≤n≤2×105, − 1 0 4 ≤ a i ≤ 1 0 4 -10^4 \leq a_i \leq 10^4 −104≤ai≤104。
题解
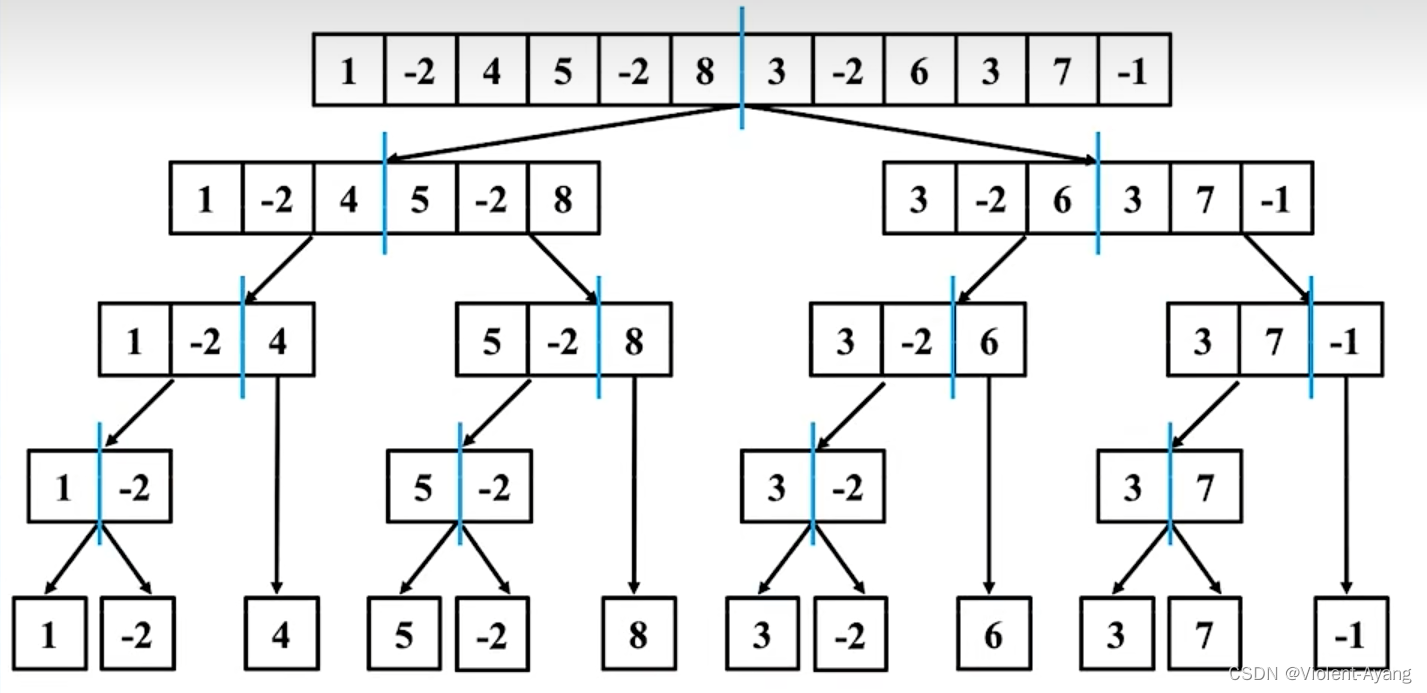
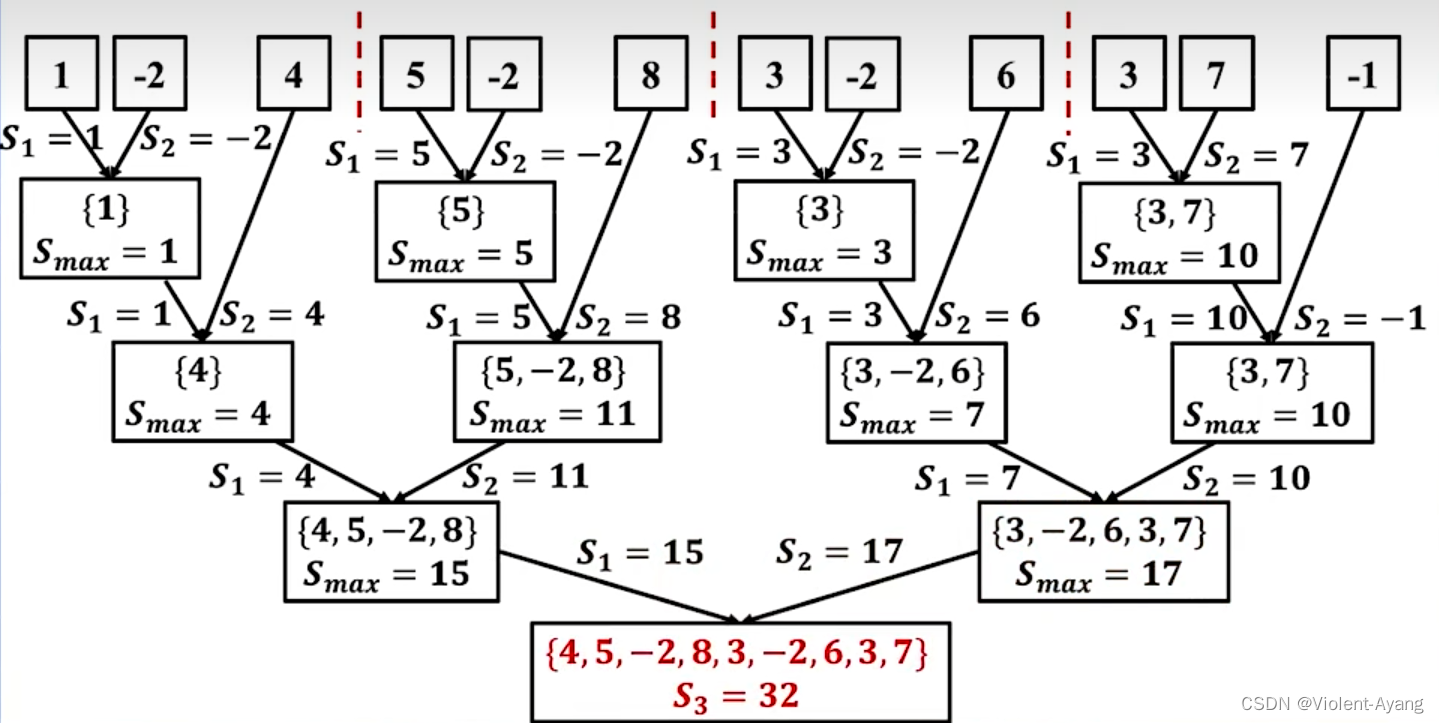
分治法的思路是这样的,其实也是分类讨论。
连续子序列的最大和主要由这三部分子区间里元素的最大和得到:
- 第 1 部分:子区间 [left, mid];
- 第 2 部分:子区间 [mid + 1, right];
- 第 3 部分:包含子区间 [mid , mid + 1] 的子区间,即 [mid] 与 [mid + 1] 一定会被选取。
对这三个部分求最大值即可。
说明:考虑第 3 部分跨越两个区间的连续子数组的时候,由于 [mid] 与 [mid + 1] 一定会被选取,可以从中间向两边扩散,扩散到底 选出最大值。
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6;
int a[N];
int crossMid(int low,int mid,int high){
int leftSum = INT32_MIN,sum = 0;
for(int i = mid;i >= low;i --){
sum += a[i];
if(sum > leftSum) leftSum = sum;
}
int rightSum = INT32_MIN;
sum = 0;
for(int i = mid+1;i <= high;i ++){
sum += a[i];
if(sum > rightSum) rightSum = sum;
}
return leftSum+rightSum;
}
int maxSubArray(int low,int high){
if(low == high) return a[low];
int mid = (low+high)/2;
int leftSum = maxSubArray(low,mid);
int rightSum = maxSubArray(mid+1,high);
int midSum = crossMid(low,mid,high);
int tmp = max(leftSum,rightSum);
return max(tmp,midSum);
}
int main(){
int n;
cin >> n;
for(int i = 0;i < n;i ++) cin >> a[i];
cout << maxSubArray(0,n-1);
return 0;
}
LCR 170. 交易逆序对的总数
在股票交易中,如果前一天的股价高于后一天的股价,则可以认为存在一个「交易逆序对」。请设计一个程序,输入一段时间内的股票交易记录 record,返回其中存在的「交易逆序对」总数。
示例 1:
输入:record = [9, 7, 5, 4, 6]
输出:8
解释:交易中的逆序对为 (9, 7), (9, 5), (9, 4), (9, 6), (7, 5), (7, 4), (7, 6), (5, 4)。
限制:
0 <= record.length <= 50000
同类问题:
逆序对
题目描述
猫猫 TOM 和小老鼠 JERRY 最近又较量上了,但是毕竟都是成年人,他们已经不喜欢再玩那种你追我赶的游戏,现在他们喜欢玩统计。
最近,TOM 老猫查阅到一个人类称之为“逆序对”的东西,这东西是这样定义的:对于给定的一段正整数序列,逆序对就是序列中 a i > a j a_i>a_j ai>aj 且 i < j i<j i<j 的有序对。知道这概念后,他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。注意序列中可能有重复数字。
Update:数据已加强。
输入格式
第一行,一个数 n n n,表示序列中有 n n n个数。
第二行 n n n 个数,表示给定的序列。序列中每个数字不超过 1 0 9 10^9 109。
输出格式
输出序列中逆序对的数目。
样例 #1
样例输入 #1
6
5 4 2 6 3 1
样例输出 #1
11
提示
对于 25 % 25\% 25% 的数据, n ≤ 2500 n \leq 2500 n≤2500
对于 50 % 50\% 50% 的数据, n ≤ 4 × 1 0 4 n \leq 4 \times 10^4 n≤4×104。
对于所有数据, n ≤ 5 × 1 0 5 n \leq 5 \times 10^5 n≤5×105
请使用较快的输入输出
应该不会 O ( n 2 ) O(n^2) O(n2) 过 50 万吧 by chen_zhe
题解
逆序对统计:
- 终止条件:当 ( l >=r ) 时,代表子数组长度为 1,此时终止划分。
- 递归划分:计算数组中点 ( m ),递归划分左子数组
reverseCount(l, m)和右子数组reverseCount(m + 1, r)。 - 合并与逆序对统计:
a. 暂存数组a闭区间 ([l, r]) 内的元素至辅助数组tmp;
b. 循环合并:设置双指针i,j分别指向左/右子数组的首元素;- 当 ( i = m + 1 ) 时:代表左子数组已合并完,因此添加右子数组当前元素
tmp[j],并执行 ( j = j + 1 ); - 否则,当 ( j = r + 1 ) 时:代表右子数组已合并完,因此添加左子数组当前元素
tmp[i],并执行 ( i = i + 1 ); - 否则,当
tmp[i]≤tmp[j]时:添加左子数组当前元素tmp[i],并执行 ( i = i + 1 ); - 否则(即
tmp[i] > tmp[j])时:添加右子数组当前元素tmp[j]并执行 ( j = j + 1 );此时构成 ( m - i + 1 ) 个「逆序对」,统计添加至res。
- 当 ( i = m + 1 ) 时:代表左子数组已合并完,因此添加右子数组当前元素
- 返回值:返回直至目前的逆序对总数
res。
#include <iostream>
#include <cstdio>
using namespace std;
const int MAXN = 5010000;
int n, a[MAXN], tmp[MAXN];
long long reverseCount(int l, int r) {
if (l >= r) return 0;
int m = (l + r) / 2;
long long res = reverseCount(l, m) + reverseCount(m + 1, r);
int i = l, j = m + 1;
for (int k = l; k <= r; k++) tmp[k] = a[k];
for (int k = l; k <= r; k++) {
if (i > m) { // 左子数组已完全复制
a[k] = tmp[j++];
} else if (j > r || tmp[i] <= tmp[j]) {
a[k] = tmp[i++];
} else {
a[k] = tmp[j++];
res += (m - i + 1); // 计算逆序对数量
}
}
return res;
}
int main() {
cin >> n;
for (int i = 0; i < n; i++) cin >> a[i];
printf("%lld\n", reverseCount(0, n - 1));
return 0;
}
进阶问题
2884. 逆序对
暑假到了,小可可和伙伴们来到海边度假,距离海滩不远的地方有个小岛,叫做欢乐岛,整个岛是一个大游乐园,里面有很多很好玩的益智游戏。
碰巧岛上正在举行“解谜题赢取免费门票”的活动,只要猜出来迷题,那么小可可和他的朋友就能在欢乐岛上免费游玩两天。
迷题是这样的:给出一串全部是正整数的数字,这些正整数都在一个范围内选取,谁能最快求出这串数字中“逆序对”的个数,那么大奖就是他的啦!
当然、主办方不可能就这么简单的让迷题被解开,数字串都是被处理过的,一部分数字被故意隐藏起来,这些数字均用 −1
来代替,想要获得大奖就必须求出被处理的数字串中最少能有多少个逆序对。
小可可很想获得免费游玩游乐园的机会,你能帮助他吗?
注:“逆序对”就是如果有两个数 A 和 B,A 在 B 左边且 A 大于 B,我们就称这两个数为一个“逆序对”。
例如: 4 2 1 3 3 里面包含了 5 个逆序对:(4,2)、(4,1)、(4,3)、(4,3)、(2,1)。
假设这串数字由 5 个正整数组成,其中任一数字 N 均在 1∼4 之间,数字串中一部分数字被 −1 替代后,如:4 2 -1 -1 3,那么这串数字,可能是 4 2 1 3 3,也可能是 4 2 4 4 3,也可能是别的样子。
你要做的就是根据已知的数字,推断出这串数字里最少能有多少个逆序对。
输入格式
第一行两个正整数 N 和 K。
第二行 N 个整数,每个都是 −1 或是一个在 1∼K之间的数。
输出格式
一个正整数,即这些数字里最少的逆序对个数。
数据范围
1≤N≤10000
,
1≤K≤100
输入样例:
5 4
4 2 -1 -1 3
输出样例:
4
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
int dp[N][110],n,a[N],ans,k;
int t1[110],t2[110],cnt;
void add(int tr[],int x,int c){
for(int i=x;i<=k;i+=i&-i)tr[i]+=c;
}
int sum(int tr[],int x){
int ans=0;
for(int i=x;i;i-=i&-i)ans+=tr[i];
return ans;
}
signed main(){
cin>>n>>k;
for(int i=1;i<=n;i++){
cin>>a[i];
if(a[i]!=-1)
add(t1,a[i],1);
}
for(int i=n;i>=1;i--){
if(a[i]!=-1){
ans+=sum(t2,a[i]-1);
add(t2,a[i],1);
add(t1,a[i],-1);
}
else{
cnt++;
for(int j=1;j<=k;j++)
dp[cnt][j]=dp[cnt-1][j]+sum(t2,j-1)+sum(t1,k)-sum(t1,j);
dp[cnt][k+1]=1e9;
for(int j=k;j>=1;j--)
dp[cnt][j]=min(dp[cnt][j],dp[cnt][j+1]);
}
}
int mi=1e9;
for(int i=1;i<=k;i++)mi=min(mi,dp[cnt][i]);
cout<<ans+mi;
}