学到这里的大家应该都非常清楚贪心算法到底是怎么一回事了,说白了就是动态规划的一种特例,没有动态规划的使用范围广,但是效率却比动态规划效率高,贪心算法不考虑之前的情况,只考虑当前的最优选择以期达到最优的结果。
目录
##买卖股票售卖的最佳时机
##买卖股票的最佳时机Ⅱ
##买卖股票售卖的最佳时机
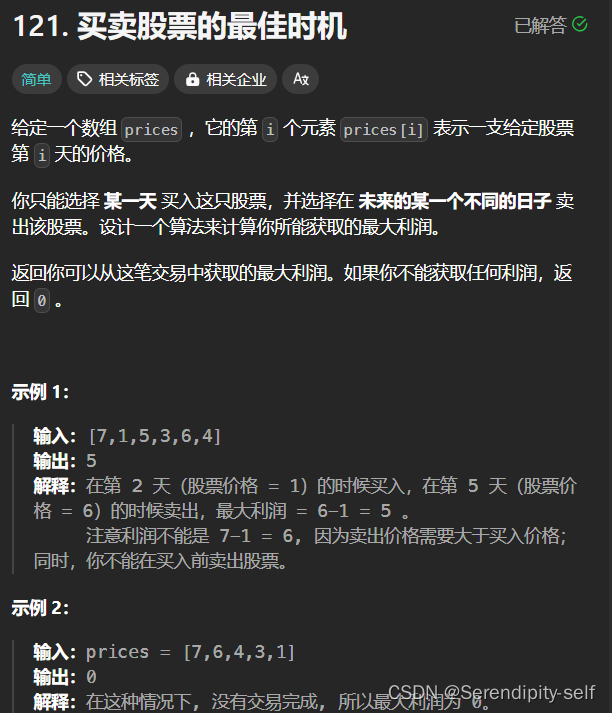
121. 买卖股票的最佳时机 - 力扣(LeetCode)
可以将整个问题进行简化说明,就是在某一天买了一支股票在这天之后的某天将这支股票再给卖出,以期获得最大的利润。
##代码示例+思路
只需要确定最小的左边界和更新右边界减去当前最小的左边界
//c++代码示例 class Solution { public: int maxProfit(vector<int>& prices) { //不存在利润的情况 if (prices.size() < 2) { return 0 ; } //存在利润的情况 //最小的利润为0 int ans = 0 ; //将第一支股票设为当前的最小值 int mins = prices[0] ; for (int i = 1 ; i < prices.size() ; i++) { //更新答案 ans = max(ans,prices[i] - mins) ; //更新最小值,我们所说的左边界 mins = min(mins,prices[i]) ; } return ans ; } };#python代码示例 class Solution: def maxProfit(self, prices: List[int]) -> int: #借助一个列表,不断往后更新答案,增加了额外开销 if len(prices) < 2 : return 0 dp = [0] * (len(prices)) mins = prices[0] for i in range(1,len(prices)) : dp[i] = max(dp[i-1],prices[i] - mins) mins = min(mins,prices[i]) return dp[-1]
##买卖股票的最佳时机Ⅱ
122. 买卖股票的最佳时机 II - 力扣(LeetCode)
可以在某一天买入或者卖出,同一天的买入和卖出可以不用考虑因为始终为0。
可以在某一天买入然后再后某一天再卖出(次数不限),以期获得最大利润。
##代码示例+思路
如果是一个递增的股票序列[1,3,5,6],我们现在思考什么时候会有最大利润呢,本天的情况我们不需要考虑,只需要考虑当天及之后的天数对利润的影响,3 - 1 + 5 - 3 + 6 - 5 = 6 - 1 ;
因此我们得到一个结论,只要后一支股票比当前支股票大,直接卖出即可。
//c++代码示例 class Solution { public: int maxProfit(vector<int>& prices) { if (prices.size() < 2 ) { return 0 ; } int ans = 0 ; for (int i = 1 ; i < prices.size() ; i++) { if (prices[i] > prices[i - 1]) { ans += prices[i] - prices[i - 1] ; } } return ans ; } };当然我们也可以采用动态规划来解决当前这个问题,因为贪心仅仅是动态规划的一种特例。
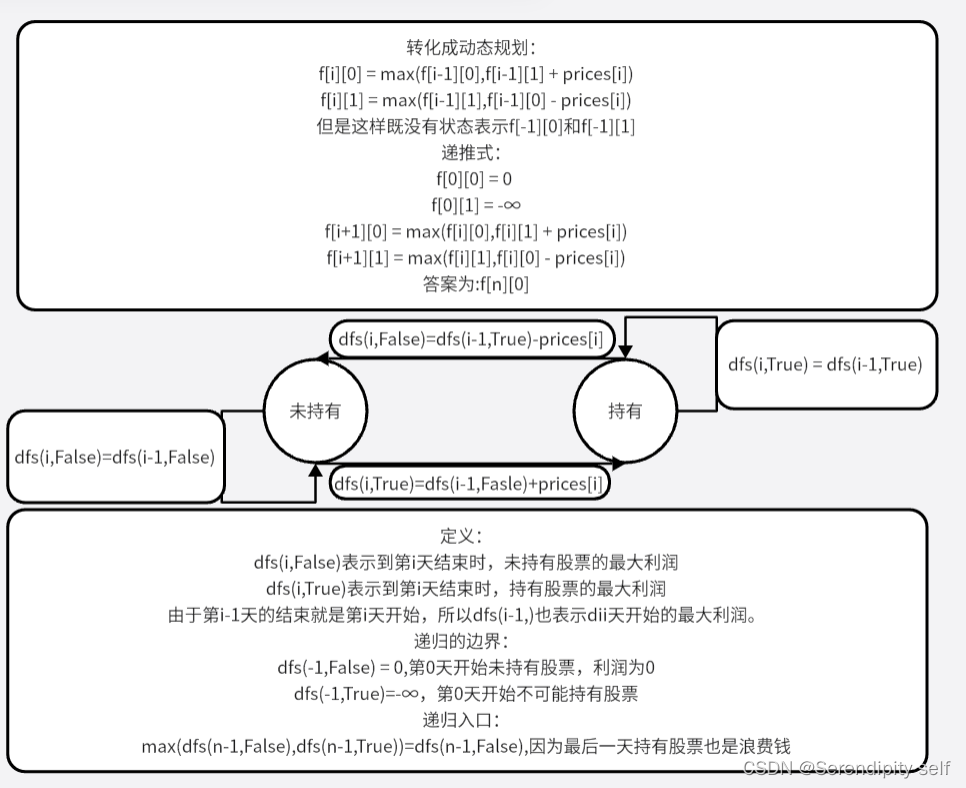
动态规划我们又该怎么考虑该问题呢?
我们可以考虑是否持有股票的状态来进行此类问题的解决-我们通常称为简单的状态dp。
#python代码示例 class Solution: def maxProfit(self, prices: List[int]) -> int: n = len(prices) @cache def dfs(i , hold) : if i < 0 : return -inf if hold else 0 if hold : return max(dfs(i-1,True),dfs(i-1,False)-prices[i]) else : return max(dfs(i-1,False),dfs(i-1,True) + prices[i]) return dfs(n-1,False)#python代码示例 class Solution: def maxProfit(self, prices: List[int]) -> int: n = len(prices) f = [[0] * 2 for _ in range(n+1)] f[0][1] = -inf for i , p in enumerate(prices) : f[i+1][0] = max(f[i][0],f[i][1] + p) f[i+1][1] = max(f[i][1],f[i][0] - p) return f[n][0]//c++代码示例 class Solution { public: int maxProfit(vector<int>& prices) { int n = prices.size(),f[n+1][2] ; memset(f,0,sizeof(f)) ; f[0][1] = INT_MIN ; for (int i = 0 ; i < n ; i++) { f[i+1][0] = max(f[i][0],f[i][1] + prices[i]) ; f[i+1][1] = max(f[i][1],f[i][0] - prices[i]) ; } return f[n][0] ; } };//c++代码示例 class Solution { public: int maxProfit(vector<int>& prices) { int n = prices.size() , memo[n][2] ; memset(memo,-1,sizeof(memo)) ; function<int(int,bool)> dfs = [&](int i , bool hold)->int { if (i < 0) { return hold ? INT_MIN : 0 ; } int &res = memo[i][hold] ; if (res != -1) { return res ; } if (hold) { return res = max(dfs(i-1,true),dfs(i-1,false)-prices[i]) ; } else { return res = max(dfs(i-1,false),dfs(i-1,true) + prices[i]) ; } }; return dfs(n-1,false) ; } };







![【RabbitMQ基础】-RabbitMQ:初识MQ[1]](https://img-blog.csdnimg.cn/direct/fa0097887382451587ba7a0e560e9d13.png)