Lecture 6: Generative Models
生成模型 vs 判别模型
判别模型(Discriminative Models)
判别模型的主要任务是直接学习输入 x x x 和类别 y y y 之间的关系。它们不关心数据的生成过程,而是直接估计类别的边界。
- 定义:判别模型直接学习 p ( y ∣ x ) p(y|x) p(y∣x),即在给定输入 x x x 的情况下,属于某个类别 y y y 的概率。
- 目标:判别模型的目标是找到一个决策边界,将不同类别的数据点分开。
判别模型的类型
-
逻辑回归(Logistic Regression):
- 逻辑回归是一种经典的判别模型,通过逻辑函数将输入映射到类别概率。
- 公式: p ( y = 1 ∣ x ) = 1 1 + e − ( β 0 + β 1 x 1 + β 2 x 2 + . . . + β n x n ) p(y=1|x) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_n x_n)}} p(y=1∣x)=1+e−(β0+β1x1+β2x2+...+βnxn)1
- 优点:计算简单,解释性强,适用于二分类问题。
-
线性判别分析(Linear Discriminant Analysis, LDA):
- LDA通过假设不同类别的数据服从同一方差但不同均值的高斯分布来实现分类。
- 优点:在数据服从高斯分布的情况下效果较好。
-
支持向量机(Support Vector Machines, SVM):
- SVM通过找到最大化类别间隔的超平面进行分类。
- 优点:对高维数据有效,具有良好的泛化能力。
-
神经网络(Neural Networks):
- 神经网络通过多层感知器和非线性激活函数学习复杂的输入输出关系。
- 优点:适用于非线性和复杂的分类问题。
生成模型
生成模型试图描述数据是如何生成的,即建模 p ( x ∣ y ) p(x|y) p(x∣y)。通过了解每个类别的数据分布,可以使用贝叶斯规则进行分类。
- 定义:生成模型学习 p ( x ∣ y ) p(x|y) p(x∣y),即在给定类别 y y y 的情况下,数据 x x x 的分布。
- 目标:生成模型的目标是通过建模数据生成过程,来进行分类。
比较
-
判别模型:
- 优点:直接优化分类任务,计算效率高,分类性能好。
- 缺点:不建模数据生成过程,缺乏对数据的深入理解。
-
生成模型:
- 优点:建模数据生成过程,处理缺失数据和小样本学习更有效,提供数据解释。
- 缺点:计算复杂度高,需要估计更多参数,在高维空间难以实现。
最大似然估计(Maximum Likelihood)
最大似然估计(Maximum Likelihood Estimation, MLE)是一种广泛应用于统计学和机器学习中的参数估计方法。它通过最大化观测数据在给定模型下的似然函数,来估计模型的参数。
我的理解:通过观测的数据推测模型(数据分布模型)参数
定义
在统计建模中,我们通常假设观测数据来自某个分布,该分布由一组未知参数 θ \theta θ 参数化。给定一组独立同分布(i.i.d.)的观测数据 S = { x 1 , x 2 , . . . , x n } S = \{x_1, x_2, ..., x_n\} S={x1,x2,...,xn},似然函数 L ( θ ) L(\theta) L(θ) 定义为在参数 θ \theta θ 下,观测到数据 S S S 的概率:
L ( θ ; S ) = p ( S ∣ θ ) = ∏ i = 1 n p ( x i ∣ θ ) L(\theta; S) = p(S|\theta) = \prod_{i=1}^n p(x_i|\theta) L(θ;S)=p(S∣θ)=i=1∏np(xi∣θ)
为了简化计算,通常使用对数似然函数(Log-Likelihood)来替代似然函数。对数似然函数定义为似然函数的对数:
L ( θ ; S ) = log L ( θ ; S ) = ∑ i = 1 n log p ( x i ∣ θ ) \mathcal{L}(\theta; S) = \log L(\theta; S) = \sum_{i=1}^n \log p(x_i|\theta) L(θ;S)=logL(θ;S)=i=1∑nlogp(xi∣θ)
最大似然估计的目标是找到一组参数 θ \theta θ,使得对数似然函数达到最大值。换句话说,MLE方法通过优化以下目标函数来估计参数:
θ ^ = arg max θ L ( θ ; S ) \hat{\theta} = \arg\max_{\theta} \mathcal{L}(\theta; S) θ^=argθmaxL(θ;S)
例题:伯努利分布的最大似然估计
伯努利分布描述了只有两个可能结果的随机变量,例如抛硬币。假设我们有一个伯努利分布的观测数据集 S = { x 1 , x 2 , . . . , x n } S = \{x_1, x_2, ..., x_n\} S={x1,x2,...,xn},其中每个 x i x_i xi 只能取值0或1。
-
参数化:伯努利分布由参数 θ \theta θ 参数化,其中 θ \theta θ 表示结果为1的概率。
-
似然函数:
L ( θ ; S ) = ∏ i = 1 n p ( x i ∣ θ ) = ∏ i = 1 n θ x i ( 1 − θ ) 1 − x i L(\theta; S) = \prod_{i=1}^n p(x_i|\theta) = \prod_{i=1}^n \theta^{x_i} (1 - \theta)^{1 - x_i} L(θ;S)=i=1∏np(xi∣θ)=i=1∏nθxi(1−θ)1−xi
- 对数似然函数:
L ( θ ; S ) = ∑ i = 1 n log p ( x i ∣ θ ) = ∑ i = 1 n [ x i log θ + ( 1 − x i ) log ( 1 − θ ) ] \mathcal{L}(\theta; S) = \sum_{i=1}^n \log p(x_i|\theta) = \sum_{i=1}^n [x_i \log \theta + (1 - x_i) \log (1 - \theta)] L(θ;S)=i=1∑nlogp(xi∣θ)=i=1∑n[xilogθ+(1−xi)log(1−θ)]
- 求解最大似然估计:
对 θ \theta θ 求导并设置导数为零,得到:
∂ L ( θ ; S ) ∂ θ = ∑ i = 1 n [ x i θ − 1 − x i 1 − θ ] = 0 \frac{\partial \mathcal{L}(\theta; S)}{\partial \theta} = \sum_{i=1}^n \left[ \frac{x_i}{\theta} - \frac{1 - x_i}{1 - \theta} \right] = 0 ∂θ∂L(θ;S)=i=1∑n[θxi−1−θ1−xi]=0
解得:
θ ^ = 1 n ∑ i = 1 n x i \hat{\theta} = \frac{1}{n} \sum_{i=1}^n x_i θ^=n1i=1∑nxi
例题:正态分布的最大似然估计
假设观测数据来自正态分布 N ( μ , σ 2 ) \mathcal{N}(\mu, \sigma^2) N(μ,σ2),其中 μ \mu μ 和 σ 2 \sigma^2 σ2 分别表示均值和方差。
- 似然函数:
L ( μ , σ 2 ; S ) = ∏ i = 1 n 1 2 π σ 2 exp ( − ( x i − μ ) 2 2 σ 2 ) L(\mu, \sigma^2; S) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(x_i - \mu)^2}{2\sigma^2} \right) L(μ,σ2;S)=i=1∏n2πσ21exp(−2σ2(xi−μ)2)
- 对数似然函数:
L ( μ , σ 2 ; S ) = ∑ i = 1 n log [ 1 2 π σ 2 exp ( − ( x i − μ ) 2 2 σ 2 ) ] \mathcal{L}(\mu, \sigma^2; S) = \sum_{i=1}^n \log \left[ \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(x_i - \mu)^2}{2\sigma^2} \right) \right] L(μ,σ2;S)=i=1∑nlog[2πσ21exp(−2σ2(xi−μ)2)]
展开对数,得到:
L ( μ , σ 2 ; S ) = − n 2 log ( 2 π σ 2 ) − 1 2 σ 2 ∑ i = 1 n ( x i − μ ) 2 \mathcal{L}(\mu, \sigma^2; S) = -\frac{n}{2} \log (2\pi\sigma^2) - \frac{1}{2\sigma^2} \sum_{i=1}^n (x_i - \mu)^2 L(μ,σ2;S)=−2nlog(2πσ2)−2σ21i=1∑n(xi−μ)2
- 求解最大似然估计:
对 μ \mu μ 和 σ 2 \sigma^2 σ2 求导并设置导数为零,得到:
∂ L ( μ , σ 2 ; S ) ∂ μ = 1 σ 2 ∑ i = 1 n ( x i − μ ) = 0 \frac{\partial \mathcal{L}(\mu, \sigma^2; S)}{\partial \mu} = \frac{1}{\sigma^2} \sum_{i=1}^n (x_i - \mu) = 0 ∂μ∂L(μ,σ2;S)=σ21i=1∑n(xi−μ)=0
解得:
μ ^ = 1 n ∑ i = 1 n x i \hat{\mu} = \frac{1}{n} \sum_{i=1}^n x_i μ^=n1i=1∑nxi
对 σ 2 \sigma^2 σ2 求导并设置导数为零,得到:
∂ L ( μ , σ 2 ; S ) ∂ σ 2 = − n 2 σ 2 + 1 2 σ 4 ∑ i = 1 n ( x i − μ ) 2 = 0 \frac{\partial \mathcal{L}(\mu, \sigma^2; S)}{\partial \sigma^2} = -\frac{n}{2\sigma^2} + \frac{1}{2\sigma^4} \sum_{i=1}^n (x_i - \mu)^2 = 0 ∂σ2∂L(μ,σ2;S)=−2σ2n+2σ41i=1∑n(xi−μ)2=0
解得:
σ ^ 2 = 1 n ∑ i = 1 n ( x i − μ ^ ) 2 \hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \hat{\mu})^2 σ^2=n1i=1∑n(xi−μ^)2
这意味着正态分布的最大似然估计为观测数据的均值和方差。
Naive Bayes
Naive Bayes 是一种基于贝叶斯定理的分类算法,广泛应用于生成模型的背景中。这里的“朴素”(Naive)是指假设特征在给定类别标签的情况下是条件独立的,这一假设在实际中通常并不完全成立。
贝叶斯定理
贝叶斯定理提供了一种在获得更多证据或信息时更新对某一假设的概率估计的方法。其表达式如下:
p ( y ∣ x ) = p ( x ∣ y ) p ( y ) p ( x ) p(y|x) = \frac{p(x|y)p(y)}{p(x)} p(y∣x)=p(x)p(x∣y)p(y)
其中:
- p ( y ∣ x ) p(y|x) p(y∣x) 是在给定特征 x x x 的情况下类别 y y y 的后验概率。
- p ( x ∣ y ) p(x|y) p(x∣y) 是在类别 y y y 给定的情况下特征 x x x 出现的可能性(似然)。
- p ( y ) p(y) p(y) 是类别 y y y 的先验概率。
- p ( x ) p(x) p(x) 是特征 x x x 的总概率。
在分类问题中,我们希望找到使后验概率最大的类别 y y y:
y ^ = arg max y p ( y ∣ x ) \hat{y} = \arg \max_{y} p(y|x) y^=argymaxp(y∣x)
根据贝叶斯定理,可以转换为:
y ^ = arg max y p ( x ∣ y ) p ( y ) p ( x ) \hat{y} = \arg \max_{y} \frac{p(x|y)p(y)}{p(x)} y^=argymaxp(x)p(x∣y)p(y)
由于 p ( x ) p(x) p(x) 对于所有类别 y y y 是相同的,我们可以简化为:
y ^ = arg max y p ( x ∣ y ) p ( y ) \hat{y} = \arg \max_{y} p(x|y)p(y) y^=argymaxp(x∣y)p(y)
朴素贝叶斯假设
朴素贝叶斯分类器的关键假设是特征在给定类别的情况下是条件独立的。这一假设极大地简化了模型的复杂性,使得计算变得更加高效。具体地,假设特征 x x x 由 d d d 个属性组成 x = ( x 1 , x 2 , . . . , x d ) x = (x_1, x_2, ..., x_d) x=(x1,x2,...,xd),在给定类别 y y y 的情况下,我们有:
p ( x ∣ y ) = ∏ i = 1 d p ( x i ∣ y ) p(x|y) = \prod_{i=1}^{d} p(x_i|y) p(x∣y)=i=1∏dp(xi∣y)
这样,我们可以将分类问题的后验概率表示为:
y ^ = arg max y p ( y ) ∏ i = 1 d p ( x i ∣ y ) \hat{y} = \arg \max_{y} p(y) \prod_{i=1}^{d} p(x_i|y) y^=argymaxp(y)i=1∏dp(xi∣y)
朴素贝叶斯分类器的学习步骤
-
估计先验概率 p ( y ) p(y) p(y):
先验概率可以通过在训练数据中每个类别的频率来估计:p ( y ) = N y N p(y) = \frac{N_y}{N} p(y)=NNy
其中, N y N_y Ny 是类别 y y y 的样本数, N N N 是总样本数。
-
估计条件概率 p ( x i ∣ y ) p(x_i|y) p(xi∣y):
条件概率可以通过在类别 y y y 的样本中每个特征值的频率来估计。对于离散特征:p ( x i ∣ y ) = N x i , y N y p(x_i|y) = \frac{N_{x_i, y}}{N_y} p(xi∣y)=NyNxi,y
其中, N x i , y N_{x_i, y} Nxi,y 是类别 y y y 中特征 x i x_i xi 的出现次数。
对于连续特征,通常假设其服从某种分布(例如正态分布),通过最大似然估计来确定分布的参数。
-
分类:
对于一个新的样本 x x x,计算每个类别的后验概率,并选择后验概率最大的类别作为预测结果。y ^ = arg max y p ( y ) ∏ i = 1 d p ( x i ∣ y ) \hat{y} = \arg \max_{y} p(y) \prod_{i=1}^{d} p(x_i|y) y^=argymaxp(y)i=1∏dp(xi∣y)
例题:垃圾邮件分类
让我们以垃圾邮件分类为例说明朴素贝叶斯分类器的具体应用。假设我们有一个训练集,包含每封邮件的文本和类别标签(垃圾邮件或非垃圾邮件)。
-
准备数据:
将每封邮件的文本表示为词袋模型,即每个词在邮件中是否出现(0 或 1)。 -
估计参数:
- 计算先验概率:计算垃圾邮件和非垃圾邮件在训练集中各自的比例。
- 计算条件概率:对于每个词,计算其在垃圾邮件和非垃圾邮件中的出现概率。
-
分类新邮件:
对于一封新邮件,计算其属于垃圾邮件和非垃圾邮件的后验概率,选择概率较大的一类作为预测结果。
例如,假设我们有如下训练数据:
- 训练集包含1000封邮件,其中400封是垃圾邮件(类1),600封是非垃圾邮件(类0)。
- 词汇表包含10,000个词。
我们计算先验概率:
p
(
Y
=
1
)
=
400
1000
=
0.4
p(Y=1) = \frac{400}{1000} = 0.4
p(Y=1)=1000400=0.4
p
(
Y
=
0
)
=
600
1000
=
0.6
p(Y=0) = \frac{600}{1000} = 0.6
p(Y=0)=1000600=0.6
接着,计算每个词在垃圾邮件和非垃圾邮件中的条件概率。例如,某个词 “free” 在400封垃圾邮件中出现了200次,在600封非垃圾邮件中出现了50次:
p
(
free
∣
Y
=
1
)
=
200
400
=
0.5
p(\text{free}|Y=1) = \frac{200}{400} = 0.5
p(free∣Y=1)=400200=0.5
p
(
free
∣
Y
=
0
)
=
50
600
≈
0.083
p(\text{free}|Y=0) = \frac{50}{600} \approx 0.083
p(free∣Y=0)=60050≈0.083
对于一封包含词 “free” 的新邮件 x x x,其后验概率可以表示为:
p
(
Y
=
1
∣
x
)
∝
p
(
Y
=
1
)
⋅
p
(
free
∣
Y
=
1
)
=
0.4
⋅
0.5
=
0.2
p(Y=1|x) \propto p(Y=1) \cdot p(\text{free}|Y=1) = 0.4 \cdot 0.5 = 0.2
p(Y=1∣x)∝p(Y=1)⋅p(free∣Y=1)=0.4⋅0.5=0.2
p
(
Y
=
0
∣
x
)
∝
p
(
Y
=
0
)
⋅
p
(
free
∣
Y
=
0
)
=
0.6
⋅
0.083
≈
0.05
p(Y=0|x) \propto p(Y=0) \cdot p(\text{free}|Y=0) = 0.6 \cdot 0.083 \approx 0.05
p(Y=0∣x)∝p(Y=0)⋅p(free∣Y=0)=0.6⋅0.083≈0.05
因此,我们将该邮件分类为垃圾邮件(类1)。
潜在变量和期望最大化算法(EM)
在统计模型和机器学习中,潜在变量(latent variables)是那些在观察数据中未直接观测到但对数据的生成有重要影响的变量。期望最大化(Expectation-Maximization, EM)算法是一种处理含有潜在变量的模型的流行方法。EM算法通过交替估计潜在变量的分布和模型参数,逐步提高模型的似然函数值,从而找到参数的最大似然估计(MLE)。
我的理解:最大似然法在某些情况无法通过求log的导数一步到位求到最大值,EM有点类似于一步一步迭代直到收敛的最大似然法。
潜在变量概述
潜在变量有时也称为隐藏变量,它们在许多生成模型中扮演重要角色。一个典型的例子是高斯混合模型(Gaussian Mixture Model, GMM),其中数据点被认为是由多个高斯分布中的一个生成的,但我们并不知道每个数据点具体来自哪个高斯分布。
高斯混合模型的数学表示如下:
p
(
x
)
=
∑
y
=
1
k
p
(
Y
=
y
)
p
(
x
∣
Y
=
y
)
=
∑
y
=
1
k
π
y
N
(
x
∣
μ
y
,
Σ
y
)
p(x) = \sum_{y=1}^{k} p(Y=y) p(x|Y=y) = \sum_{y=1}^{k} \pi_y \mathcal{N}(x|\mu_y, \Sigma_y)
p(x)=y=1∑kp(Y=y)p(x∣Y=y)=y=1∑kπyN(x∣μy,Σy)
其中:
- x x x 是观测数据。
- y y y 是潜在变量,表示数据点属于哪个高斯分布(即哪个簇)。
- π y \pi_y πy 是第 y y y 个高斯分布的混合系数(该簇的先验概率)。
- N ( x ∣ μ y , Σ y ) \mathcal{N}(x|\mu_y, \Sigma_y) N(x∣μy,Σy) 是以 μ y \mu_y μy 为均值, Σ y \Sigma_y Σy 为协方差矩阵的高斯分布。
在这种模型中,潜在变量 y y y 是我们不知道的,但它影响了 x x x 的生成过程。EM算法就是为了解决这样的含有潜在变量的问题而设计的。
期望最大化算法(EM)
EM算法是Dempster, Laird和Rubin于1977年提出的,用于寻找含有潜在变量的模型的最大似然估计。EM算法的核心思想是通过交替的两个步骤——期望步骤(E-step)和最大化步骤(M-step),不断优化参数估计,直至收敛。
-
E步(期望步骤):
在这个步骤中,给定当前模型参数,计算潜在变量的期望值。这一步是基于当前参数对潜在变量的后验分布进行估计。Q i ( t + 1 ) = p θ ( t ) ( Y = y ∣ X = x i ) = π y ( t ) N ( x i ∣ μ y ( t ) , Σ y ( t ) ) ∑ y ′ π y ′ ( t ) N ( x i ∣ μ y ′ ( t ) , Σ y ′ ( t ) ) Q_i^{(t+1)} = p_{\theta^{(t)}}(Y=y|X=x_i) = \frac{\pi_y^{(t)} \mathcal{N}(x_i|\mu_y^{(t)}, \Sigma_y^{(t)})}{\sum_{y'} \pi_{y'}^{(t)} \mathcal{N}(x_i|\mu_{y'}^{(t)}, \Sigma_{y'}^{(t)})} Qi(t+1)=pθ(t)(Y=y∣X=xi)=∑y′πy′(t)N(xi∣μy′(t),Σy′(t))πy(t)N(xi∣μy(t),Σy(t))
-
M步(最大化步骤):
在这个步骤中,利用E步中计算的期望值,重新估计模型参数。这一步的目标是最大化期望的对数似然函数。π y ( t + 1 ) = 1 n ∑ i = 1 n Q i ( t + 1 ) \pi_y^{(t+1)} = \frac{1}{n} \sum_{i=1}^{n} Q_i^{(t+1)} πy(t+1)=n1i=1∑nQi(t+1)
μ y ( t + 1 ) = ∑ i = 1 n Q i ( t + 1 ) x i ∑ i = 1 n Q i ( t + 1 ) \mu_y^{(t+1)} = \frac{\sum_{i=1}^{n} Q_i^{(t+1)} x_i}{\sum_{i=1}^{n} Q_i^{(t+1)}} μy(t+1)=∑i=1nQi(t+1)∑i=1nQi(t+1)xi
Σ y ( t + 1 ) = ∑ i = 1 n Q i ( t + 1 ) ( x i − μ y ( t + 1 ) ) ( x i − μ y ( t + 1 ) ) T ∑ i = 1 n Q i ( t + 1 ) \Sigma_y^{(t+1)} = \frac{\sum_{i=1}^{n} Q_i^{(t+1)} (x_i - \mu_y^{(t+1)}) (x_i - \mu_y^{(t+1)})^T}{\sum_{i=1}^{n} Q_i^{(t+1)}} Σy(t+1)=∑i=1nQi(t+1)∑i=1nQi(t+1)(xi−μy(t+1))(xi−μy(t+1))T
EM算法的过程如下:
- 初始化参数 θ ( 0 ) = ( π y ( 0 ) , μ y ( 0 ) , Σ y ( 0 ) ) \theta^{(0)} = (\pi_y^{(0)}, \mu_y^{(0)}, \Sigma_y^{(0)}) θ(0)=(πy(0),μy(0),Σy(0))。
- 重复以下步骤直到收敛:
- E步:计算潜在变量的后验分布 Q i ( t + 1 ) Q_i^{(t+1)} Qi(t+1)。
- M步:更新参数 θ ( t + 1 ) \theta^{(t+1)} θ(t+1)。
例题:高斯混合模型EM求分布
假设我们有一个二维数据集,这些数据点是从两个不同的高斯分布中生成的。我们希望使用高斯混合模型(GMM)来对这些数据点进行聚类,并估计两个高斯分布的参数(均值和协方差矩阵)以及每个数据点属于哪个分布的概率。
假设我们有如下数据点(为了简化起见,数据点数量较少):
| 数据点 x \mathbf{x} x | x 1 x_1 x1 | x 2 x_2 x2 |
|---|---|---|
| x 1 \mathbf{x}_1 x1 | 1.0 | 2.0 |
| x 2 \mathbf{x}_2 x2 | 1.5 | 1.8 |
| x 3 \mathbf{x}_3 x3 | 5.0 | 8.0 |
| x 4 \mathbf{x}_4 x4 | 6.0 | 8.5 |
| x 5 \mathbf{x}_5 x5 | 1.2 | 1.9 |
| x 6 \mathbf{x}_6 x6 | 5.5 | 7.8 |
可以看到,数据点大致分布在两个簇上:一个在靠近(1, 2)的区域,另一个在靠近(5, 8)的区域。
我们将使用EM算法来拟合一个包含两个成分(即两个高斯分布)的高斯混合模型。以下是详细步骤:
假设我们初始化两个高斯分布的参数如下:
- 均值向量 μ 1 = ( 1.0 , 2.0 ) \mu_1 = (1.0, 2.0) μ1=(1.0,2.0), μ 2 = ( 5.0 , 8.0 ) \mu_2 = (5.0, 8.0) μ2=(5.0,8.0)
- 协方差矩阵 Σ 1 = ( 1.0 0.0 0.0 1.0 ) \Sigma_1 = \begin{pmatrix} 1.0 & 0.0 \\ 0.0 & 1.0 \end{pmatrix} Σ1=(1.00.00.01.0), Σ 2 = ( 1.0 0.0 0.0 1.0 ) \Sigma_2 = \begin{pmatrix} 1.0 & 0.0 \\ 0.0 & 1.0 \end{pmatrix} Σ2=(1.00.00.01.0)
- 混合系数 π 1 = 0.5 \pi_1 = 0.5 π1=0.5, π 2 = 0.5 \pi_2 = 0.5 π2=0.5
第二步:E步(期望步骤)
计算每个数据点属于每个高斯分布的概率(后验概率),使用当前参数进行计算。
对于数据点 x i \mathbf{x}_i xi,后验概率 Q i ( t + 1 ) Q_i^{(t+1)} Qi(t+1) 的计算公式为:
Q i ( t + 1 ) = p ( Y = y ∣ X = x i ) = π y ( t ) N ( x i ∣ μ y ( t ) , Σ y ( t ) ) ∑ y ′ π y ′ ( t ) N ( x i ∣ μ y ′ ( t ) , Σ y ′ ( t ) ) Q_i^{(t+1)} = p(Y=y|X=\mathbf{x}_i) = \frac{\pi_y^{(t)} \mathcal{N}(\mathbf{x}_i|\mu_y^{(t)}, \Sigma_y^{(t)})}{\sum_{y'} \pi_{y'}^{(t)} \mathcal{N}(\mathbf{x}_i|\mu_{y'}^{(t)}, \Sigma_{y'}^{(t)})} Qi(t+1)=p(Y=y∣X=xi)=∑y′πy′(t)N(xi∣μy′(t),Σy′(t))πy(t)N(xi∣μy(t),Σy(t))
N ( x ∣ μ y , Σ y ) = 1 ( 2 π ) d / 2 ∣ Σ y ∣ 1 / 2 exp ( − 1 2 ( x − μ y ) ⊤ Σ y − 1 ( x − μ y ) ) \mathcal{N}(\mathbf{x} | \mu_y, \Sigma_y) = \frac{1}{(2\pi)^{d/2} |\Sigma_y|^{1/2}} \exp \left( -\frac{1}{2} (\mathbf{x} - \mu_y)^\top \Sigma_y^{-1} (\mathbf{x} - \mu_y) \right) N(x∣μy,Σy)=(2π)d/2∣Σy∣1/21exp(−21(x−μy)⊤Σy−1(x−μy))
假设经过计算得到如下结果(简化示例):
| 数据点 x \mathbf{x} x | Q i 1 Q_{i1} Qi1 | Q i 2 Q_{i2} Qi2 |
|---|---|---|
| x 1 \mathbf{x}_1 x1 | 0.9 | 0.1 |
| x 2 \mathbf{x}_2 x2 | 0.85 | 0.15 |
| x 3 \mathbf{x}_3 x3 | 0.2 | 0.8 |
| x 4 \mathbf{x}_4 x4 | 0.1 | 0.9 |
| x 5 \mathbf{x}_5 x5 | 0.88 | 0.12 |
| x 6 \mathbf{x}_6 x6 | 0.3 | 0.7 |
第三步:M步(最大化步骤)
利用E步中的后验概率,重新估计高斯分布的参数。
混合系数:
π y ( t + 1 ) = 1 n ∑ i = 1 n Q i ( t + 1 ) \pi_y^{(t+1)} = \frac{1}{n} \sum_{i=1}^{n} Q_i^{(t+1)} πy(t+1)=n1i=1∑nQi(t+1)
均值向量:
μ y ( t + 1 ) = ∑ i = 1 n Q i ( t + 1 ) x i ∑ i = 1 n Q i ( t + 1 ) \mu_y^{(t+1)} = \frac{\sum_{i=1}^{n} Q_i^{(t+1)} \mathbf{x}_i}{\sum_{i=1}^{n} Q_i^{(t+1)}} μy(t+1)=∑i=1nQi(t+1)∑i=1nQi(t+1)xi
协方差矩阵:
Σ y ( t + 1 ) = ∑ i = 1 n Q i ( t + 1 ) ( x i − μ y ( t + 1 ) ) ( x i − μ y ( t + 1 ) ) ⊤ ∑ i = 1 n Q i ( t + 1 ) \Sigma_y^{(t+1)} = \frac{\sum_{i=1}^{n} Q_i^{(t+1)} (\mathbf{x}_i - \mu_y^{(t+1)}) (\mathbf{x}_i - \mu_y^{(t+1)})^\top}{\sum_{i=1}^{n} Q_i^{(t+1)}} Σy(t+1)=∑i=1nQi(t+1)∑i=1nQi(t+1)(xi−μy(t+1))(xi−μy(t+1))⊤
假设计算结果如下:
- 新的混合系数: π 1 = 0.67 \pi_1 = 0.67 π1=0.67, π 2 = 0.33 \pi_2 = 0.33 π2=0.33
- 新的均值向量: μ 1 = ( 1.23 , 1.92 ) \mu_1 = (1.23, 1.92) μ1=(1.23,1.92), μ 2 = ( 5.25 , 8.1 ) \mu_2 = (5.25, 8.1) μ2=(5.25,8.1)
- 新的协方差矩阵:
Σ 1 = ( 0.1 0.01 0.01 0.1 ) , Σ 2 = ( 0.2 0.02 0.02 0.2 ) \Sigma_1 = \begin{pmatrix} 0.1 & 0.01 \\ 0.01 & 0.1 \end{pmatrix}, \Sigma_2 = \begin{pmatrix} 0.2 & 0.02 \\ 0.02 & 0.2 \end{pmatrix} Σ1=(0.10.010.010.1),Σ2=(0.20.020.020.2)
重复E步和M步,直到参数不再显著变化(即收敛)。每次迭代都会提高模型的对数似然值,使得模型越来越适合数据。
Lecture 7: Multiple Classifier Systems
此讲义大纲旨在概述多分类器系统及其在提高分类器性能中的重要角色。
偏差-方差
-
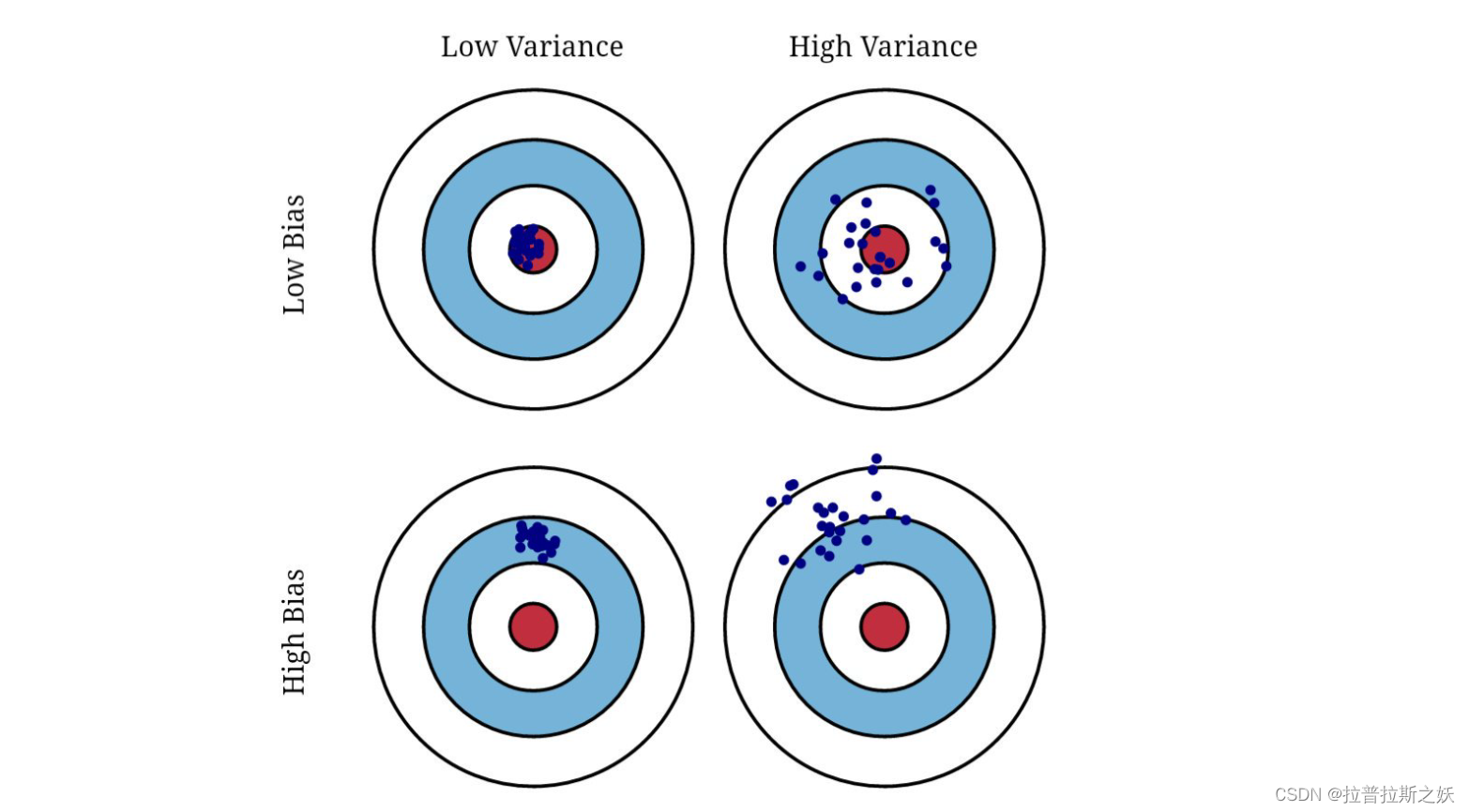
偏差(Bias):指模型预测的期望值与真实值之间的差异。高偏差通常意味着模型过于简单,无法捕捉数据的底层模式。

-
方差(Variance):指模型预测的离散程度,即模型在不同训练集上的表现差异。高方差通常意味着模型过于复杂,对训练数据的噪声敏感,容易过拟合。

-
低偏差高方差模型:复杂度高的模型(如深度神经网络),能够很好地拟合训练数据,偏差较低,但对训练数据的噪声敏感,方差较高,容易过拟合。
-
高偏差低方差模型:简单的模型(如线性回归),无法很好地拟合训练数据,偏差较高,但对训练数据的噪声不敏感,方差较低,容易欠拟合。
Ensemble Methods
集成方法(Ensemble Methods)是机器学习中的一种技术,通过结合多个分类器的预测结果,来提升整体模型的性能。集成方法利用了“群体智慧”的理念,认为多个独立且多样化的分类器组合在一起,其表现通常优于单个分类器。
集成方法的优点
提高准确率:通过组合多个模型的预测,可以减少单个模型可能带来的误差,提高整体预测的准确性。
减少过拟合:单个模型容易对训练数据过拟合,集成方法通过结合多个模型,可以缓解过拟合问题。
增强鲁棒性:集成方法可以提高模型对噪声和异常值的鲁棒性,使其在不同的数据集上表现更加稳定。
Combining Outputs
在多分类器系统中,输出组合(Combining Outputs)是一个关键步骤,通过适当的策略将多个分类器的预测结果结合起来,可以显著提高整体模型的性能。输出组合的方法有多种,本文将详细介绍其中的几种常见方法,包括简单平均、加权平均和简单多数投票。
Bagging(Bootstrap Aggregating)(减少方差)
Bagging,即Bootstrap Aggregating,是一种通过减少模型方差来提升模型性能的集成学习方法。它的基本思想是通过对训练数据集进行有放回抽样(bootstrap sampling),生成多个不同的子数据集,并在每个子数据集上训练一个模型。最终,通过对这些模型的预测结果进行平均或投票来得到更稳定和准确的预测结果。Bagging 尤其适用于高方差的模型,如决策树。
Bagging 的步骤
Bagging 的具体实施步骤如下:
-
生成多个子数据集:
- 从原始训练数据集 ( S = {(x_1, y_1), \ldots, (x_n, y_n)} ) 中有放回地抽取多个子数据集 ( S_b ),每个子数据集的大小与原始数据集相同。
-
训练多个模型:
- 对每个子数据集 ( S_b ) 训练一个模型 ( h_b )。
-
聚合模型的预测结果:
- 对于回归问题,通过对所有模型的预测结果进行平均:
[ \hat{h}(x) = \frac{1}{B} \sum_{b=1}^{B} h_b(x) ] - 对于分类问题,通过对所有模型的预测结果进行多数投票:
[ \hat{h}(x) = \text{argmax}c \left( \sum{b=1}^{B} \mathbb{I}(h_b(x) = c) \right) ]
其中,(\mathbb{I}(h_b(x) = c)) 是一个指示函数,当 ( h_b(x) ) 预测为类别 ( c ) 时,其值为 1,否则为 0。
- 对于回归问题,通过对所有模型的预测结果进行平均:
Bagging 的理论基础

Bagging 的应用与优势
Bagging 在实际应用中具有以下优势:
- 减少方差:通过聚合多个模型的预测结果,Bagging 能有效减少模型的方差,提高泛化能力。
- 增强稳定性:Bagging 对数据中的噪声和异常值不敏感,因为每个模型只在部分数据上训练,个别异常值对整体模型影响较小。
- 适用于高方差模型:Bagging 特别适用于高方差、低偏差的模型,如决策树和神经网络。
Bagging 的经典应用之一是随机森林(Random Forest),它通过对决策树应用 Bagging,并在每个决策树的节点上随机选择部分特征进行分裂,从而进一步减少模型的方差,提高性能。
Boosting(减少偏差和方差)
Boosting的基本概念
-
弱分类器:弱分类器是指那些表现比随机猜测稍好的分类器。在二分类问题中,弱分类器的准确率要高于50%。常见的例子包括决策树桩(单层决策树)。
-
Boosting过程:Boosting算法以迭代的方式工作。在每次迭代中,它会调整误分类实例的权重,使得这些实例在下一次迭代中得到更多关注。最终,多个弱分类器的组合能够显著提高分类精度。
自适应Boosting(AdaBoost)
- 初始化:给每个训练样本一个相等的权重 w 1 ( i ) = 1 n w_1(i) = \frac{1}{n} w1(i)=n1。
- 迭代训练:对于每一轮迭代
k
k
k:
- 训练弱分类器
h
k
h_k
hk,以最小化加权误分类率
ϵ
k
\epsilon_k
ϵk:
ϵ k = ∑ i = 1 n w k ( i ) δ ( y i ≠ h k ( x i ) ) ∑ i = 1 n w k ( i ) \epsilon_k = \frac{\sum_{i=1}^n w_k(i) \delta(y_i \neq h_k(x_i))}{\sum_{i=1}^n w_k(i)} ϵk=∑i=1nwk(i)∑i=1nwk(i)δ(yi=hk(xi)) - 计算分类器的权重
α
k
\alpha_k
αk:
α k = 0.5 log 1 − ϵ k ϵ k \alpha_k = 0.5 \log \frac{1 - \epsilon_k}{\epsilon_k} αk=0.5logϵk1−ϵk - 更新样本权重:
w k + 1 ( i ) = w k ( i ) exp ( − α k y i h k ( x i ) ) w_{k+1}(i) = w_k(i) \exp(-\alpha_k y_i h_k(x_i)) wk+1(i)=wk(i)exp(−αkyihk(xi))
- 训练弱分类器
h
k
h_k
hk,以最小化加权误分类率
ϵ
k
\epsilon_k
ϵk:
- 最终分类器:加权投票得到最终分类器:
H ( x ) = sign ( ∑ k = 1 K α k h k ( x ) ) H(x) = \text{sign} \left( \sum_{k=1}^K \alpha_k h_k(x) \right) H(x)=sign(k=1∑Kαkhk(x))
例题:Adaboost
我们将通过一个简单的例子来演示AdaBoost算法的整个过程。假设我们有一个二分类问题,并且数据集如下:
| 样本 | 特征 x 1 x_1 x1 | 特征 x 2 x_2 x2 | 类别 y y y |
|---|---|---|---|
| 1 | 1 | 2 | +1 |
| 2 | 2 | 3 | +1 |
| 3 | 3 | 3 | -1 |
| 4 | 4 | 5 | -1 |
我们将使用决策树桩(单层决策树)作为弱分类器。
首先,初始化每个样本的权重
w
1
(
i
)
w_1(i)
w1(i) 为相等值:
w
1
(
i
)
=
1
4
=
0.25
w_1(i) = \frac{1}{4} = 0.25
w1(i)=41=0.25
第一步:训练第一个弱分类器
假设我们选择 x 1 ≤ 1.5 x_1 \leq 1.5 x1≤1.5 作为第一个决策桩的决策规则:
| 样本 | 特征 x 1 x_1 x1 | 特征 x 2 x_2 x2 | 类别 y y y | 分类结果 h 1 ( x ) h_1(x) h1(x) | 误分类 | 权重 w 1 w_1 w1 |
|---|---|---|---|---|---|---|
| 1 | 1 | 2 | +1 | +1 | 否 | 0.25 |
| 2 | 2 | 3 | +1 | -1 | 是 | 0.25 |
| 3 | 3 | 3 | -1 | -1 | 否 | 0.25 |
| 4 | 4 | 5 | -1 | -1 | 否 | 0.25 |
计算第一个分类器的加权误分类率
ϵ
1
\epsilon_1
ϵ1:
ϵ
1
=
∑
i
=
1
4
w
1
(
i
)
⋅
δ
(
y
i
≠
h
1
(
x
i
)
)
=
0.25
⋅
1
=
0.25
\epsilon_1 = \sum_{i=1}^4 w_1(i) \cdot \delta(y_i \neq h_1(x_i)) = 0.25 \cdot 1 = 0.25
ϵ1=i=1∑4w1(i)⋅δ(yi=h1(xi))=0.25⋅1=0.25
计算第一个分类器的权重
α
1
\alpha_1
α1:
α
1
=
0.5
log
1
−
ϵ
1
ϵ
1
=
0.5
log
1
−
0.25
0.25
=
0.5
log
3
≈
0.5493
\alpha_1 = 0.5 \log \frac{1 - \epsilon_1}{\epsilon_1} = 0.5 \log \frac{1 - 0.25}{0.25} = 0.5 \log 3 \approx 0.5493
α1=0.5logϵ11−ϵ1=0.5log0.251−0.25=0.5log3≈0.5493
更新每个样本的权重
w
2
(
i
)
w_2(i)
w2(i):
w
2
(
i
)
=
w
1
(
i
)
exp
(
−
α
1
y
i
h
1
(
x
i
)
)
w_2(i) = w_1(i) \exp(-\alpha_1 y_i h_1(x_i))
w2(i)=w1(i)exp(−α1yih1(xi))
对于误分类的样本2:
w
2
(
2
)
=
0.25
exp
(
0.5493
)
≈
0.4082
w_2(2) = 0.25 \exp(0.5493) \approx 0.4082
w2(2)=0.25exp(0.5493)≈0.4082
对于正确分类的样本1, 3, 4:
w
2
(
1
)
=
0.25
exp
(
−
0.5493
)
≈
0.1518
w_2(1) = 0.25 \exp(-0.5493) \approx 0.1518
w2(1)=0.25exp(−0.5493)≈0.1518
w
2
(
3
)
=
0.25
exp
(
−
0.5493
)
≈
0.1518
w_2(3) = 0.25 \exp(-0.5493) \approx 0.1518
w2(3)=0.25exp(−0.5493)≈0.1518
w
2
(
4
)
=
0.25
exp
(
−
0.5493
)
≈
0.1518
w_2(4) = 0.25 \exp(-0.5493) \approx 0.1518
w2(4)=0.25exp(−0.5493)≈0.1518
归一化权重:
w
2
(
i
)
=
w
2
(
i
)
∑
i
=
1
4
w
2
(
i
)
w_2(i) = \frac{w_2(i)}{\sum_{i=1}^4 w_2(i)}
w2(i)=∑i=14w2(i)w2(i)
∑
i
=
1
4
w
2
(
i
)
=
0.1518
+
0.4082
+
0.1518
+
0.1518
=
0.8636
\sum_{i=1}^4 w_2(i) = 0.1518 + 0.4082 + 0.1518 + 0.1518 = 0.8636
i=1∑4w2(i)=0.1518+0.4082+0.1518+0.1518=0.8636
w
2
(
1
)
=
0.1518
0.8636
≈
0.176
w_2(1) = \frac{0.1518}{0.8636} \approx 0.176
w2(1)=0.86360.1518≈0.176
w
2
(
2
)
=
0.4082
0.8636
≈
0.473
w_2(2) = \frac{0.4082}{0.8636} \approx 0.473
w2(2)=0.86360.4082≈0.473
w
2
(
3
)
=
0.1518
0.8636
≈
0.176
w_2(3) = \frac{0.1518}{0.8636} \approx 0.176
w2(3)=0.86360.1518≈0.176
w
2
(
4
)
=
0.1518
0.8636
≈
0.176
w_2(4) = \frac{0.1518}{0.8636} \approx 0.176
w2(4)=0.86360.1518≈0.176
第二步:训练第二个弱分类器
使用更新后的权重 w 2 ( i ) w_2(i) w2(i),选择一个新的决策桩。假设我们选择 x 1 ≤ 2.5 x_1 \leq 2.5 x1≤2.5 作为第二个决策桩的决策规则:
| 样本 | 特征 x 1 x_1 x1 | 特征 x 2 x_2 x2 | 类别 y y y | 分类结果 h 2 ( x ) h_2(x) h2(x) | 误分类 | 权重 w 2 w_2 w2 |
|---|---|---|---|---|---|---|
| 1 | 1 | 2 | +1 | +1 | 否 | 0.176 |
| 2 | 2 | 3 | +1 | +1 | 否 | 0.473 |
| 3 | 3 | 3 | -1 | -1 | 否 | 0.176 |
| 4 | 4 | 5 | -1 | -1 | 否 | 0.176 |
计算第二个分类器的加权误分类率
ϵ
2
\epsilon_2
ϵ2:
ϵ
2
=
∑
i
=
1
4
w
2
(
i
)
⋅
δ
(
y
i
≠
h
2
(
x
i
)
)
=
0
\epsilon_2 = \sum_{i=1}^4 w_2(i) \cdot \delta(y_i \neq h_2(x_i)) = 0
ϵ2=i=1∑4w2(i)⋅δ(yi=h2(xi))=0
由于分类器完全正确,我们可以看到其误分类率为0,因此我们继续调整权重:
α 2 = 0.5 log 1 − ϵ 2 ϵ 2 \alpha_2 = 0.5 \log \frac{1 - \epsilon_2}{\epsilon_2} α2=0.5logϵ21−ϵ2
由于 ϵ 2 = 0 \epsilon_2 = 0 ϵ2=0,这意味着分类器是完美的。我们可以停止在此,因为我们已经找到了一个完美的分类器。
最终分类器
假设我们需要多个弱分类器的加权组合来构建最终的分类器,我们可以将这些弱分类器组合起来:
H ( x ) = sign ( α 1 h 1 ( x ) + α 2 h 2 ( x ) ) H(x) = \text{sign} \left( \alpha_1 h_1(x) + \alpha_2 h_2(x) \right) H(x)=sign(α1h1(x)+α2h2(x))
在此示例中,我们实际上在第二步已经找到了一个完美分类器,因此我们可以直接使用第二个弱分类器作为最终分类器。
Boosting的优势和应用
-
减少偏差和方差:通过对误分类样本的反复调整,Boosting能够显著减少模型的偏差。同时,由于它是通过组合多个分类器的结果,Boosting也能够减少方差。
-
鲁棒性强:Boosting对噪声数据有一定的抵抗能力,特别是在AdaBoost中,每个分类器只需要比随机猜测略好,因此即使某些弱分类器表现较差,整体性能仍然能够提升。
-
广泛应用:Boosting被广泛应用于各种分类任务,包括图像识别、文本分类和生物信息学等领域。其灵活性和高效性使得它在实际应用中非常受欢迎。
Lecture 8: Theoretical Foundation of Machine Learning
集中不等式(Concentration Inequalities)
1. 集中不等式的背景和重要性
在机器学习中,模型的估计误差不仅依赖于训练数据,还依赖于数据集的随机波动。集中不等式帮助我们量化这种随机波动,特别是当涉及到大规模数据时,可以确保模型的性能有一定的保证。
2. Hoeffding不等式
定义
Hoeffding不等式是最基础和常用的集中不等式之一,主要用于界定一组独立随机变量的和与其期望值之间的偏差。
定理(Hoeffding’s Inequality)
设
X
1
,
X
2
,
…
,
X
n
X_1, X_2, \ldots, X_n
X1,X2,…,Xn 是取值范围在
[
a
,
b
]
[a, b]
[a,b] 之间的独立同分布随机变量。对于任意
ϵ
>
0
\epsilon > 0
ϵ>0,有:
P
{
E
[
X
]
−
1
n
∑
i
=
1
n
X
i
≥
ϵ
}
≤
exp
(
−
2
n
ϵ
2
(
b
−
a
)
2
)
\mathbb{P}\left\{ \mathbb{E}[X] - \frac{1}{n} \sum_{i=1}^n X_i \geq \epsilon \right\} \leq \exp\left( -\frac{2n\epsilon^2}{(b-a)^2} \right)
P{E[X]−n1i=1∑nXi≥ϵ}≤exp(−(b−a)22nϵ2)
P
{
E
[
X
]
−
1
n
∑
i
=
1
n
X
i
≤
−
ϵ
}
≤
exp
(
−
2
n
ϵ
2
(
b
−
a
)
2
)
\mathbb{P}\left\{ \mathbb{E}[X] - \frac{1}{n} \sum_{i=1}^n X_i \leq -\epsilon \right\} \leq \exp\left( -\frac{2n\epsilon^2}{(b-a)^2} \right)
P{E[X]−n1i=1∑nXi≤−ϵ}≤exp(−(b−a)22nϵ2)
推导
Hoeffding不等式的推导基于切比雪夫不等式和Chernoff界限,具体推导过程涉及复杂的概率论和不等式理论,在此不详述。其核心思想是通过界定偏差,得出概率界限,从而为模型性能提供可靠保证。
应用
Hoeffding不等式广泛应用于统计学习理论中的估计误差分析,尤其是用于分析经验风险最小化中的偏差界限。在实际应用中,它帮助我们理解在有限样本条件下,模型估计的稳定性和可靠性。
3. McDiarmid不等式
定义
McDiarmid不等式是一种更广泛的集中不等式,适用于一类更一般的函数,其变化受限于每个输入变量的变化。
定理(McDiarmid’s Inequality)
设
X
1
,
X
2
,
…
,
X
n
X_1, X_2, \ldots, X_n
X1,X2,…,Xn 是
n
n
n 个独立随机变量,且存在常数
c
c
c,使得对于所有
i
i
i 及任何
x
i
,
x
i
′
∈
X
x_i, x_i' \in X
xi,xi′∈X,函数
f
:
X
n
→
R
f: X^n \to \mathbb{R}
f:Xn→R 满足以下有界增量条件:
∣
f
(
x
1
,
…
,
x
i
,
…
,
x
n
)
−
f
(
x
1
,
…
,
x
i
′
,
…
,
x
n
)
∣
≤
c
|f(x_1, \ldots, x_i, \ldots, x_n) - f(x_1, \ldots, x_i', \ldots, x_n)| \leq c
∣f(x1,…,xi,…,xn)−f(x1,…,xi′,…,xn)∣≤c
对于任意
ϵ
>
0
\epsilon > 0
ϵ>0,有:
P
{
f
(
X
1
,
…
,
X
n
)
−
E
[
f
(
X
1
,
…
,
X
n
)
]
≥
ϵ
}
≤
exp
(
−
2
ϵ
2
n
c
2
)
\mathbb{P}\left\{ f(X_1, \ldots, X_n) - \mathbb{E}[f(X_1, \ldots, X_n)] \geq \epsilon \right\} \leq \exp\left( -\frac{2\epsilon^2}{nc^2} \right)
P{f(X1,…,Xn)−E[f(X1,…,Xn)]≥ϵ}≤exp(−nc22ϵ2)
P
{
f
(
X
1
,
…
,
X
n
)
−
E
[
f
(
X
1
,
…
,
X
n
)
]
≤
−
ϵ
}
≤
exp
(
−
2
ϵ
2
n
c
2
)
\mathbb{P}\left\{ f(X_1, \ldots, X_n) - \mathbb{E}[f(X_1, \ldots, X_n)] \leq -\epsilon \right\} \leq \exp\left( -\frac{2\epsilon^2}{nc^2} \right)
P{f(X1,…,Xn)−E[f(X1,…,Xn)]≤−ϵ}≤exp(−nc22ϵ2)
推导
McDiarmid不等式的推导同样基于Chernoff界限和马尔可夫不等式,通过构造函数的有界增量特性,推导出其集中不等式形式。具体推导过程涉及概率论的高级技巧,主要思想是通过限制函数的增量,得出其集中性质。
应用
McDiarmid不等式在机器学习中的应用非常广泛,尤其是用于分析复杂模型的误差界限。它特别适用于那些无法直接应用Hoeffding不等式的情况,如涉及到依赖于多个变量的复杂函数。在实际应用中,McDiarmid不等式帮助我们在模型选择和评估中提供更严谨的误差分析。
统计学习理论(Statistical Learning Theory)
统计学习理论(Statistical Learning Theory)是机器学习的理论基础之一,它为理解和分析学习算法的性能提供了严格的数学框架。该理论主要探讨如何通过有限的数据样本来推断潜在的概率分布及其相应的预测函数。在本讲义中,统计学习理论涵盖了以下几个关键主题:有限基数分析、VC维度分析、覆盖数分析以及Rademacher复杂度分析。
1. 有限基数分析
定义和背景
有限基数分析探讨的是在假设空间有限的情况下,如何分析学习算法的性能。假设空间的有限性意味着我们可以枚举所有可能的假设,并计算每个假设的误差。
集中不等式在有限基数中的应用
当假设空间 H H H 的基数为有限时,我们可以使用Hoeffding不等式来界定经验误差和真实误差之间的偏差。具体而言,假设 H H H 中包含 m m m 个假设,Hoeffding不等式告诉我们,在概率至少为 1 − δ 1-\delta 1−δ 的情况下,以下不等式成立:
sup h ∈ H [ E [ h ] − E ^ [ h ] ] ≤ 2 log ( m / δ ) n \sup_{h \in H} \left[ E[h] - \hat{E}[h] \right] \leq \sqrt{\frac{2 \log(m/\delta)}{n}} h∈Hsup[E[h]−E^[h]]≤n2log(m/δ)
其中, E [ h ] E[h] E[h] 是假设 h h h 的期望误差, E ^ [ h ] \hat{E}[h] E^[h] 是假设 h h h 的经验误差, n n n 是样本数量。
2. VC维度分析
VC维度的定义
VC维度(Vapnik-Chervonenkis Dimension)是衡量假设空间复杂度的一个关键指标。对于一个假设空间 H H H,其VC维度定义为:
V C ( H ) = max { m : Π H ( m ) = 2 m } VC(H) = \max\{ m : \Pi_H(m) = 2^m \} VC(H)=max{m:ΠH(m)=2m}
其中, Π H ( m ) \Pi_H(m) ΠH(m) 表示假设空间 H H H 在 m m m 个样本点上能够产生的不同划分数。通俗地讲,VC维度表示假设空间能够完全拟合的最大样本点数。
VC维度与泛化误差
VC维度与泛化误差之间有紧密的关系。具体来说,假设 H H H 的VC维度为 d d d,则在概率至少为 1 − δ 1-\delta 1−δ 的情况下,以下不等式成立:
sup h ∈ H [ E [ h ] − E ^ [ h ] ] ≤ 4 d log ( 2 n / d ) + 4 log ( 4 / δ ) n \sup_{h \in H} \left[ E[h] - \hat{E}[h] \right] \leq \sqrt{\frac{4d \log(2n/d) + 4 \log(4/\delta)}{n}} h∈Hsup[E[h]−E^[h]]≤n4dlog(2n/d)+4log(4/δ)
这一结果表明,假设空间的VC维度越大,其复杂度越高,泛化误差的上界也越大。
3. 覆盖数分析
覆盖数的定义
覆盖数(Covering Number)是衡量假设空间复杂度的另一个指标。对于假设空间 H H H 和精度参数 η \eta η,其覆盖数 N ( H , η ) N(H, \eta) N(H,η) 定义为在 H H H 中存在的最小子集 { h 1 , h 2 , … , h m } \{h_1, h_2, \ldots, h_m\} {h1,h2,…,hm},使得对于任意的 h ∈ H h \in H h∈H,存在 h i h_i hi 满足:
sup x ∈ X ∣ h ( x ) − h i ( x ) ∣ ≤ η \sup_{x \in X} |h(x) - h_i(x)| \leq \eta x∈Xsup∣h(x)−hi(x)∣≤η
换句话说,覆盖数描述了假设空间中任意假设函数可以用精度为 η \eta η 的有限子集来近似。
覆盖数与泛化误差
覆盖数与泛化误差之间也存在重要关系。假设 H H H 的覆盖数为 N ( H , η ) N(H, \eta) N(H,η),在概率至少为 1 − δ 1-\delta 1−δ 的情况下,以下不等式成立:
sup h ∈ H [ E [ h ] − E ^ [ h ] ] ≤ η + 2 log N ( H , η ) + 2 log ( 2 / δ ) n \sup_{h \in H} \left[ E[h] - \hat{E}[h] \right] \leq \eta + \sqrt{\frac{2 \log N(H, \eta) + 2 \log(2/\delta)}{n}} h∈Hsup[E[h]−E^[h]]≤η+n2logN(H,η)+2log(2/δ)
这一结果说明了覆盖数越小,假设空间越简单,泛化误差的上界越低。
4. Rademacher复杂度分析
Rademacher复杂度的定义
Rademacher复杂度是衡量假设空间在特定数据集上的复杂度的一个数据依赖性指标。给定一个假设空间 H H H 和一个数据集 S = { x 1 , x 2 , … , x n } S = \{x_1, x_2, \ldots, x_n\} S={x1,x2,…,xn},Rademacher复杂度定义为:
R S ( H ) = E σ [ sup h ∈ H 1 n ∑ i = 1 n σ i h ( x i ) ] \mathcal{R}_S(H) = \mathbb{E}_\sigma \left[ \sup_{h \in H} \frac{1}{n} \sum_{i=1}^n \sigma_i h(x_i) \right] RS(H)=Eσ[h∈Hsupn1i=1∑nσih(xi)]
其中, σ i \sigma_i σi 是独立的Rademacher随机变量,即取值为 ± 1 \pm1 ±1 且概率相等。
Rademacher复杂度与泛化误差
Rademacher复杂度提供了一个强有力的工具来分析假设空间的泛化误差。在概率至少为 1 − δ 1-\delta 1−δ 的情况下,以下不等式成立:
sup h ∈ H [ E [ h ] − E ^ [ h ] ] ≤ 2 R S ( H ) + 3 log ( 2 / δ ) 2 n \sup_{h \in H} \left[ E[h] - \hat{E}[h] \right] \leq 2 \mathcal{R}_S(H) + 3 \sqrt{\frac{\log(2/\delta)}{2n}} h∈Hsup[E[h]−E^[h]]≤2RS(H)+32nlog(2/δ)
这一结果表明,Rademacher复杂度越低,假设空间的复杂度越低,泛化误差的上界也越低。
Lecture 8-b: Optimization Techniques
More Representations
在优化技术中,表示问题的方法有很多种,选择合适的表示方法对于问题的求解至关重要。表示方法的选择直接影响算法的效率和效果。本部分讲解了几种常见的表示方法以及它们在不同情境下的应用。
General Search Methods
通用搜索框架
通用搜索方法通常遵循一个基本框架,该框架包括以下步骤:
- 初始化:生成初始解 ( x(0) )。
- 评价:评估初始解的质量。
- 生成新解:基于当前解 ( x(t) ) 生成新解 ( x’ )。
- 选择:在新解和当前解之间选择一个更优的解作为下一步的解 ( x(t+1) )。
- 重复:重复上述过程,直到满足终止条件。
这种框架适用于多种搜索方法,不同的方法在具体的解生成和选择策略上有所区别。
典型搜索框架
局部搜索
局部搜索是一种基于当前解在其邻域中搜索更优解的方法。它包括以下几个变种:
- 贪婪搜索(Hill Climbing):每次迭代都选择邻域中最优的解。
- 随机局部搜索:在邻域中随机选择解进行搜索。
贪婪搜索(Greedy Search)之所以被称为“贪婪”,是因为它在每一步的搜索过程中总是选择当前最优的解,而不考虑未来可能会出现的更优解。这个策略表现出一种“目光短浅”的行为,只关注当前的局部最优解,而不是全局最优解。
局部搜索的优点是简单直观,适用于许多实际问题。但它容易陷入局部最优。
模拟退火(Simulated Annealing)
模拟退火是一种通过引入概率接受较差解来避免局部最优的改进方法,其核心思想来自于物理中的退火过程。其算法步骤如下:
- 初始化:生成初始解 ( x(0) ),设置初始温度 ( T(0) )。
- 迭代:在每次迭代中,基于当前解生成新解 ( x’ ),计算新解的目标函数值 ( f(x’) )。
- 接受策略:如果新解更优,则接受新解作为当前解。如果新解较差,以概率 ( p = \exp(-\Delta f / T) ) 接受新解,其中 ( \Delta f ) 是目标函数值的差异。
- 降温:逐渐降低温度 ( T ),直到达到终止条件。
在高温阶段,算法能够接受较差的解,从而具有较强的探索能力。这有助于算法跳出局部最优解,探索更广泛的解空间。随着温度的降低,算法的探索能力减弱,更倾向于在当前解的邻域内进行细致搜索,逐渐收敛到最优解。
模拟退火的优点是能够跳出局部最优,但其收敛速度较慢,且参数(如初始温度、降温策略)的选择较为复杂。
禁忌搜索(Tabu Search)
禁忌搜索通过维护一个禁忌列表来避免重复访问相同的解。其主要步骤包括:
- 初始化:生成初始解,并初始化禁忌列表。
- 生成新解:基于当前解生成新解,但避免使用禁忌列表中的解。
- 更新禁忌列表:将当前解加入禁忌列表,并根据策略更新禁忌列表。
禁忌搜索适用于复杂的组合优化问题,但禁忌列表的管理和更新策略需要精心设计。
基于种群的搜索(Population-based Search)
基于种群的搜索方法通过同时处理多个解(种群)来进行搜索。常见的方法有遗传算法(Genetic Algorithm)和进化策略(Evolutionary Strategy)。其主要步骤包括:
- 初始化种群:生成初始种群。
- 选择:根据适应度函数选择优良个体。
- 交叉和变异:通过交叉和变异操作生成新种群。
- 迭代:重复选择、交叉和变异,直到达到终止条件。
基于种群的搜索方法能够很好地探索解空间,但计算量较大,适应度函数的设计和参数选择较为复杂。
遗传算法
遗传算法是一种典型的基于种群的搜索方法,其算法步骤包括:
- 编码:将解编码为染色体(字符串或向量)。
- 初始化:生成初始种群。
- 选择:根据适应度函数选择父代个体。
- 交叉:通过交叉操作生成子代个体。
- 变异:通过变异操作引入随机性。
- 迭代:重复选择、交叉和变异,直到达到终止条件。
遗传算法适用于多种优化问题,具有较强的适应性和鲁棒性。
为什么“种群”可能是有益的?
-
平滑效果
种群方法的一个显著优势是其平滑效果。具体来说,使用种群的方法可以使原始目标函数变得更加平滑。这是因为种群中的个体在搜索空间内分布较广,可以减少陷入局部最优的可能性,从而更好地探索全局最优解。例如,在高斯分布的情况下,适当的超参数(如方差)可以使搜索过程更为有效。 -
多样性保持
种群方法可以保持搜索过程中个体的多样性。相比单点搜索方法(如贪婪算法或模拟退火算法),种群方法能够同时探索多个方向,从而更有可能找到全局最优解。这种多样性使得种群方法在处理复杂、多模态问题时表现尤为出色。 -
分布优化
通过使用种群,优化过程可以视为在寻找一个好的概率分布(如概率密度函数的参数),从中可以采样出优质解。这种视角有助于理解和改进优化过程,因为它将优化问题转化为一个分布优化问题。 -
鲁棒性增强
种群方法的鲁棒性较高,因为其不依赖于单一解的好坏。即使某个解在某次迭代中表现不佳,只要种群中有足够多的优质解,整个搜索过程仍能顺利进行。这使得种群方法在面对不确定性和噪声时表现更为稳健。 -
适应性强
种群方法可以根据具体问题和搜索空间的特性调整其操作算子和参数。例如,通过调节选择压力、变异率和交叉率等参数,可以优化搜索过程的效率和效果。此外,不同的种群方法(如遗传算法、粒子群优化等)可以根据问题需求灵活选择。
如何使种群更加有益?
-
超参数优化
为了使种群方法达到最佳效果,必须对其超参数进行精细调节。这些超参数包括种群大小、变异率、交叉率等。通过实验和分析,可以找到适合特定问题的最佳参数组合,从而提升算法性能。 -
多次运行
假设算法已经收敛到某个(全局或局部)最优解。为了增加找到不同全局最优解的概率,可以多次运行算法,并希望每次运行的最终种群收敛到不同的最优解。这可以通过改变初始种群或调整算法参数来实现。 -
混合策略
在某些情况下,单一的种群方法可能无法充分发挥其潜力。此时,可以考虑将多种优化方法结合起来,形成混合策略。例如,可以结合局部搜索算法和种群方法,利用局部搜索的快速收敛性和种群方法的全局搜索能力,达到更优的优化效果。 -
增强多样性
为了防止种群过早收敛到局部最优解,可以采取措施增强种群的多样性。例如,可以引入自适应变异策略,根据种群的进化状态动态调整变异率,或者使用精英保留策略,在保留优质解的同时增加新个体的引入。 -
结合领域知识
在优化过程中,结合问题的领域知识可以显著提升算法性能。例如,在选择变异和交叉操作时,可以利用领域知识设计更为有效的操作算子,从而提高搜索效率和解的质量。
![【YOLOv10改进[CONV]】使用DualConv二次创新C2f模块实现轻量化 + 含全部代码和详细修改方式 + 手撕结构图 + 全网首发](https://img-blog.csdnimg.cn/direct/bfd81518969c4589841d99649a2e132f.png)





![[已解决] Android手机如何通过Wi-Fi连接电脑?](https://img-blog.csdnimg.cn/direct/1d05d72f5a544c2c9698c7ac63b1c792.png)