目录
前言
一.函数依赖相关
1.1函数依赖集F的逻辑蕴涵
1.2函数依赖集闭包
1.3函数依赖的推理规则
1.3.1独立推理规则
自反律
增广律
传递律
1.3.2其他推理规则
合并规则
分解规则
伪传递规则
二.数据集闭包与F逻辑蕴涵的充要条件
2.1属性集闭包
2.2F逻辑蕴涵的充要条件
2.3求属性集闭包算法
2.4例题
2.5算法终止条件
三.码值理论
3.1函数依赖集F的属性分类
3.2(L、R、N、LR)四类属性的定理
3.3例题
四.函数依赖集的等价和最小函数依赖集
4.1函数依赖集的覆盖与等价
4.2最小函数依赖集的定义
4.3求最小函数依赖集例题
五.关系模式的分解方法
5.1模式分解的概念
5.2分解的无损连接性判定(无损分解)
5.3分解的函数依赖保持性判定
5.4满足3NF的函数依赖保持分解算法
5.5满足3NF的函数依赖保持和无损连接的分解算法
前言
数据库讲解---(关系规范化)【一】_关系数据库规范化-CSDN博客
一.函数依赖相关
1.1函数依赖集F的逻辑蕴涵
对于一个函数依赖F的关系模式R(U,F),其任何一个关系r,若函数依赖X->Y都成立,则称F逻辑蕴涵X->Y
1.2函数依赖集闭包
称所有被一个已知函数依赖集F逻辑蕴涵的那些函数依赖的集合为F的闭包,记为F+
1.3函数依赖的推理规则
1.3.1独立推理规则
-
自反律
如果Y包含于X,则X->Y
-
增广律
如果Z包含于W,且X->Y,则XW->YZ
-
传递律
如果X->Y且Y->Z,则X->Z
1.3.2其他推理规则
-
合并规则
若X->Y,X->Z,有X->YZ
-
分解规则
X->Y,Z包含于Y,有X->Z
-
伪传递规则
X->Y,WY->Z,有XW->Z
二.数据集闭包与F逻辑蕴涵的充要条件
2.1属性集闭包

称为属性集X关于函数依赖集F的闭包
换句话说,属性X在F上的属性集闭包就是属性X能够推导出来的所有属性的集合
2.2F逻辑蕴涵的充要条件
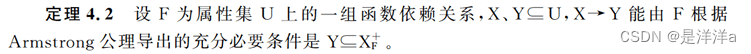
于是判断某一函数依赖X->Y能否由F根据Armstrong公理导出的问题,就转换为求:
2.3求属性集闭包算法
求:
求属性集X关于U上的函数依赖集F的闭包
步骤:

PS:“该算法计算过程是有限的,经过有限次循环后,一定会得到一个不会再次迭代的结果”
2.4例题
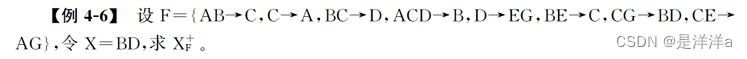
解法:
= X = BD
- 在F中搜寻所有仅由
中属性决定的函数依赖,有一个:“D->EG”,注意“ACD->B”不能算作,因为其中还包含了“AC”,此时的
= BDEG
- 在F(此时的F中已经不包含“D->EG”了)中搜寻所有仅由
中属性决定的函数依赖,有一个:“BE->C”,此时的
= BCDEG
- 在F(此时的F中已经不包含“BE->C”了)中搜寻所有仅由
中属性决定的函数依赖,有三个:“C->A、BC->D、CG->BD”,此时的
= ABCDEG
此时已经包含了F中所有属性,可以直接退出算法,此时的
就是最后所求
2.5算法终止条件
=
- 当发现
包含全部属性时
- 在F中的函数依赖的右边属性中,再也找不到
中未出现过的属性
- 在F中未用过的函数依赖的左边属性中已没有
的子集
三.码值理论
3.1函数依赖集F的属性分类
- L类:仅出现在F的函数依赖左边的属性
- R类:仅出现在F的函数依赖右边的属性
- N类:在F的函数依赖左右两边均未出现的属性
- LR类:在F的函数依赖左右两边均出现的属性
3.2(L、R、N、LR)四类属性的定理
- 对于给定关系模式R及其函数依赖集F,若X是L类属性,则X必是R的候选码的成员
- 对于给定关系模式R及其函数依赖集F,若X是N类属性,则X必是R的候选码的成员
- 对于给定关系模式R及其函数依赖集F,若X是R类属性,则X不在任何候选码中
- 对于给定关系模式R及其函数依赖集F,若X是L类或N类属性组成的属性集,且
包含R的全部属性,则X是R的唯一候选码
3.3例题
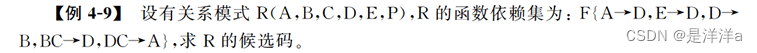
解题方法:
- 在做这种题时,我们要首先写出R的L类属性和N类属性,因为只有这两个属性才是候选码中成员
- 在这道题中,L类属性有:“CE”,N类属性有:“P”
- 因此X为:“CEP”,而
为“ABCDEP”,
包含了R的全部属性,因此“CEP”是R的唯一候选码
四.函数依赖集的等价和最小函数依赖集
4.1函数依赖集的覆盖与等价
- 设F和G是依赖集,若
=
,则称F与G等价,记为F
G
- F和G等价的充分必要条件是:“F
,且G
”
检查两个函数依赖集F合G是否等价的方法:
- 检查F中的每个函数是否属于
,若全部满足,则F
。例如:“若有X->Y
F,则计算
,若果Y
,那么X->Y
”
- 检查是否G
- 如果G
,且F
,则F与G等价
4.2最小函数依赖集的定义
如果函数依赖集F满足下列条件,则称F是一个极小函数依赖集或最小覆盖
- F中每一个函数依赖的右边都是单个属性
- 对F中任一函数依赖X->A,F-(X->A)都不与F等价
- 对于F中的任一函数依赖X->A,{F-(X->A)}∪{Z->A}都不与F等价,Z为X的任一子集
如果函数依赖集F与某个最小函数依赖集Fm等价,则称Fm是F的最小覆盖或Fm是F的最小依赖集
最小函数依赖集的求解算法:
- 检查F中的每个函数依赖X->A,若A = A1,A2,....,则根据分解规则,用X->
(i=1,2,3...,k)取代X->A
- 检查F中的每个函数依赖集X->A,令G = F - (X->A),若有A
,则从F中去掉此函数依赖
- 检查F中各函数依赖X->A,设X = B1,B2,....,Bm,检查
(i=1,2,3,...,m),当A
(X-
)时,即以X-
替换X
4.3求最小函数依赖集例题
问题:
将下列函数依赖集F划分为最小函数依赖集
![]()
解答:
- 消去F中冗余的函数依赖,即可求得最小函数依赖集
- 考察A->B,将A->B从F中删除,令X=A,则
=AC,因为B不属于
,所以A->B不冗余,保留
- 考察B->A,将B->A从F中删除,令X=B,则
=ABC,因为A属于
,所以B->A冗余,删除
- 考察B->C,将B->C从F中删除,令X=B,则
=B,因为C不属于
,所以B->C不冗余,保留
- 考察A->C,将A->C从F中删除,令X=A,则
=ABC,因为C属于
,所以A->C冗余,删除
- 考察C->A,将C->A从F中删除,令X=C,则
=C,因为A不属于
,所以C->A不冗余,保留
- 因此可以得到F2 = {A->B,B->C,C->A}
- 判断每个函数依赖左边是否有冗余属性(即判断左边属性是否仅为单属性)
- 如果首先考察B->C,那么求得F3 = {A->B,B->A,A->C,C->A}也是F的最小覆盖,因此可知函数依赖集
五.关系模式的分解方法
5.1模式分解的概念

5.2分解的无损连接性判定(无损分解)

无损分解的判定算法:
输入:
一个关系模式R(A1,A2,...,An),R上的一个函数依赖集F以及R的一个分解ρ = {{R1,F1},{R2,F2},...,{Rk,Fk}}
输出:
确定ρ是否是一个连接不失真分解
方法:
- 构造一个n列k行表,第i对应于
,第j列对应于属性
:
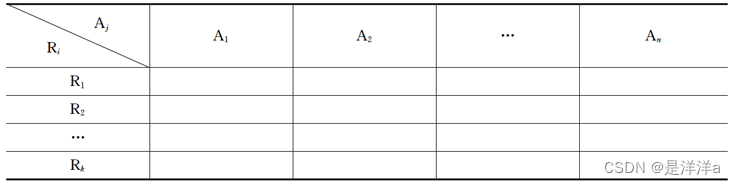
- 填表:若
则第i行第j列上填入
,否则填入
- 修改表:注意检查F中的每一个函数依赖X->Y,如果在对应于X的那些属性的所有列上X的符号相同,就使这些符号相同的行中对应于Y的那些属性的那些列上的符号也相同。即如果其中有
,则将
改为
,若没有
,则将它们全部改为
- 反复进行(3),如发现某一行变成a1,a2,....,ak,则此分解ρ具有连接不失真性
例题:
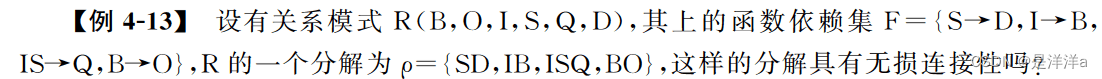
解法:
- 首先构造初始表,并填表:
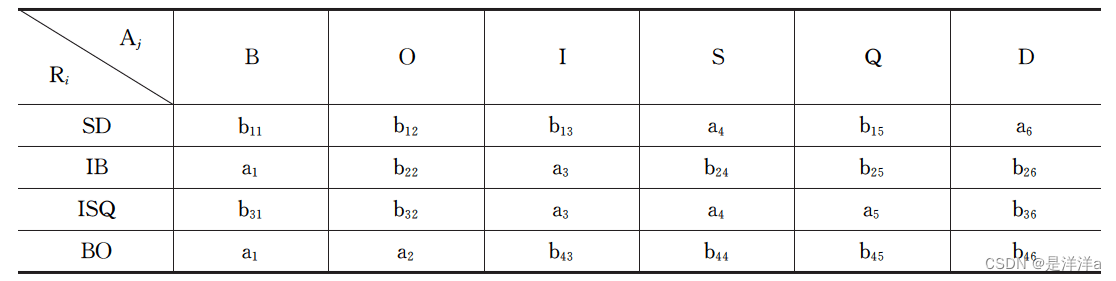
- 逐一考察函数依赖并修改表
- S->D,可以将
改为
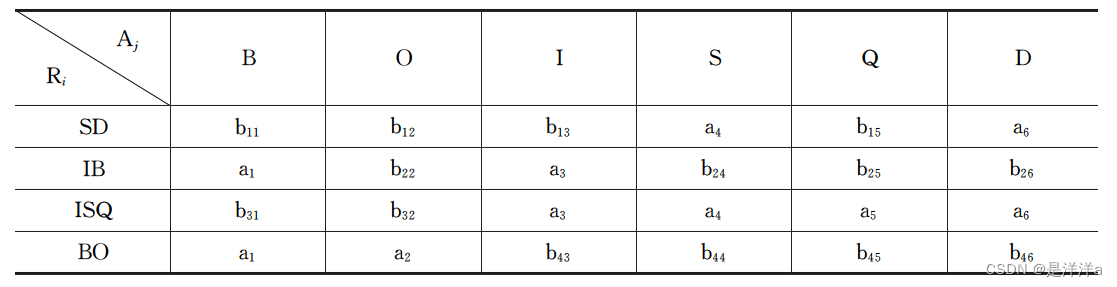
- I->B,
改为
- IS->Q,因为IS上没有值相等的行,所以不用修改表
- B->O,将
、
都改为
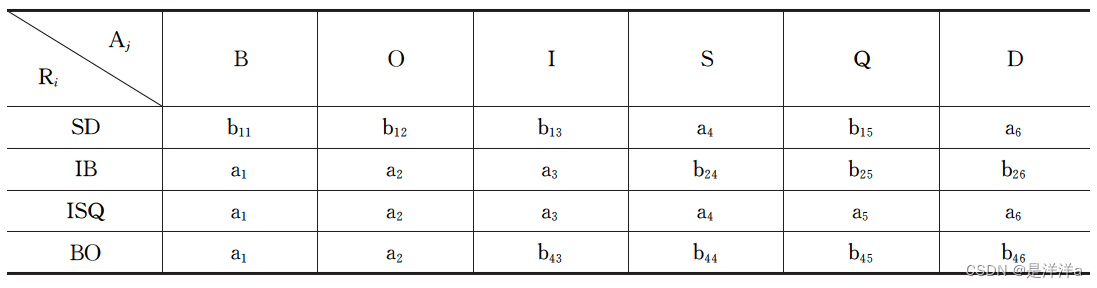
- 此时表中出现了“a1、a2、a3、a4、a5、a6”的行,所以该分解具有无损连接性
5.3分解的函数依赖保持性判定

保持依赖的判定算法:
- 检验任一个函数依赖X->Y
F是否可以用G根据Armstrong公理导出,即Y
是否成立
- 检验任一个函数依赖X->Y
G是否可以用F根据Armstrong公理导出,即Y
是否成立
- 若上述Y
与Y
均成立,则函数保持依赖
例题:

解法:

5.4满足3NF的函数依赖保持分解算法

例题:
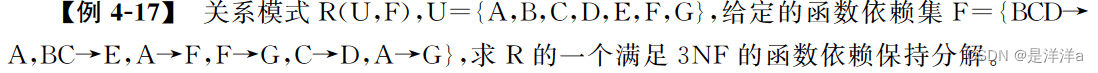
解法:

5.5满足3NF的函数依赖保持和无损连接的分解算法

例题:
解法:




![[word] word图片环绕方式怎么设置? #经验分享#笔记#媒体](https://img-blog.csdnimg.cn/img_convert/878c3f9f858731552a4a49f95b979cb0.gif)