在排序的大海上，冒泡排序像一朵花朵般绽放，
每个元素都像是水珠，跃动在涟漪的波浪中。
它们轻轻上浮，与周围的元素相比较，
若自身更大，便悄然交换位置。

这是一场缓慢的舞蹈，每一步都小心翼翼，
直到所有元素都找到了自己的位置，
像是夜空中闪烁的星星，它们最终静静地排列，
形成了一个美妙的序列，闪耀着排序的光芒。

一、冒泡排序的思想

冒泡排序的思想是通过依次比较相邻的元素，并将较大（或较小）的元素交换到右侧（或左侧），从而逐渐 “冒泡” 出最大（或最小）的元素。在每一轮排序中，都会选取一个相邻的元素对进行比较，并根据排序规则交换它们的位置，直到整个序列有序为止。这个过程像是气泡在液体中上浮一样，故得名 “冒泡排序”。

二、冒泡排序的发展历程

冒泡排序是一种经典的排序算法，其发展历程可以追溯到 20 世纪初。

1. 最初的想法：冒泡排序的基本思想可能源自人们日常生活中对物品排序的经验。比如，在洗碗时，较重的碗会沉到水底，而较轻的碗则会浮到水面，类似于冒泡排序中较大的元素会逐渐“冒泡”到序列的顶端。
2. 早期实现：冒泡排序最早的形式可能是手动进行的。人们可能会通过比较相邻的元素，并根据大小调整它们的位置，以达到排序的目的。
3. 数学描述：对冒泡排序进行更严格的数学描述和分析可能出现在 20 世纪中期，随着计算机科学的发展和对算法的研究。
4. 计算机实现：随着计算机的出现和普及，冒泡排序得到了实际的应用和实现。早期的计算机程序员可能会使用冒泡排序作为排序算法之一，因为它相对简单易懂。
5. 算法改进：随着时间的推移，人们对排序算法进行了改进和优化。尽管冒泡排序的时间复杂度较高，但它仍然具有教学和理解的价值。同时，一些改进的冒泡排序算法也被提出，以减少其时间复杂度或优化其性能。

三、冒泡排序具象化

场景假设：我们需要将下图序列使用冒泡排序按从小到大进行排序。

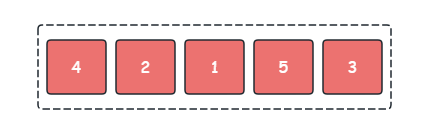
1. 第 $1$ 轮冒泡：对当前序列执行冒泡，最终元素 $5$ 交换至正确位置

2. 第 $2$ 轮冒泡：对当前序列执行冒泡，最终元素 $4$ 交换至正确位置

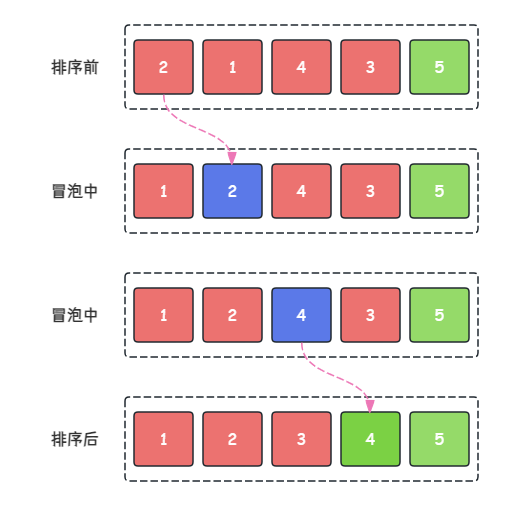
3. 第 $3$ 轮冒泡：对当前序列执行冒泡，最终元素 $3$ 交换至正确位置

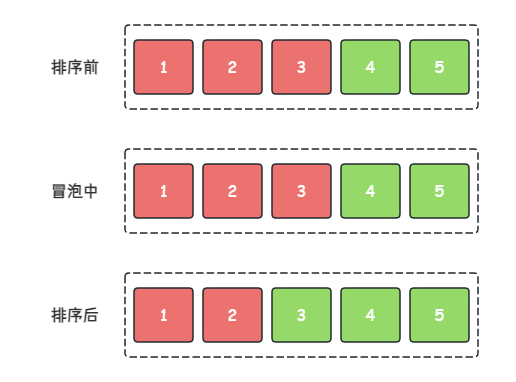
4. 第 $4$ 轮冒泡：对当前序列执行冒泡，最终元素 $2$ 交换至正确位置

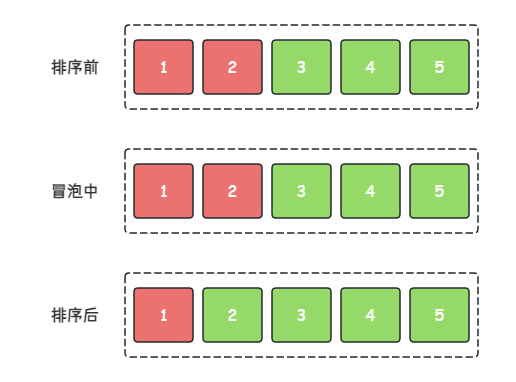
$n$ 个元素，只要 $n-1$ 个元素完成排序，最后一个元素必定处于正确的位置。

四、冒泡排序算法实现

void bubbleSort(int[] arr) {
    int n = arr.length; // 获取数组的长度

    // 外层循环控制比较轮数，每轮确定一个最大值
    for (int i = 0; i < n - 1; i++) { 

        // 内层循环控制每轮的比较次数
        for (int j = 0; j < n - i - 1; j++) { 
            if (arr[j] > arr[j + 1]) { // 如果当前元素大于下一个元素，则交换它们的位置
                // 交换 arr[j] 和 arr[j+1]
                int temp = arr[j]; // 使用临时变量 temp 存储 arr[j] 的值
                arr[j] = arr[j + 1]; // 将 arr[j+1] 的值赋给 arr[j]
                arr[j + 1] = temp; // 将 temp 中存储的 arr[j] 的值赋给 arr[j+1]
            }
        }
    }
}

算法时间复杂度分析：

情况	时间复杂度	计算公式	公式解释
最好情况	$O(n)$	$T(n)=n=O(n)$	当输入的数据已经是有序的（升序或降序），冒泡排序只需要遍历一次数组，因此最优时间复杂度是 $O(n)$
平均情况	$O(n^2)$	$T(n)={\sum }_{i=1}^{n}i=\frac{n(n+1)}{2}=O(n^2)$	在平均情况下，冒泡排序需要比较 $\frac{n(n+1)}{2}$ 次，因此平均时间复杂度是 $O(n^2)$
最坏情况	$O(n^2)$	$T(n)={\sum }_{i=1}^{n}i=\frac{n(n+1)}{2}=O(n^2)$	当输入的数据是完全逆序的，冒泡排序需要比较 $\frac{n(n+1)}{2}$ 次，因此最坏时间复杂度是 $O(n)$

五、冒泡排序的效率优化

在之前的例子中，我们发现：其实，第 $2$ 轮冒泡之后就已经排序好了。

仔细观察，我们可以发现一个规律：如果在某轮冒泡没有发生交换操作，则排序就已经完成。

因此，我们可以优化冒泡排序：

/* 优化后的冒泡排序 */
void optimizedBubbleSort(int[] nums) {
    int n = nums.length;
    boolean swapped; // 标志位：记录是否发生了元素交换

    for (int i = 0; i < n - 1; i++) {
        swapped = false; // 每轮外循环开始前，将标志位重置为 false

        // 内循环：未排序区间为 [0, n-i-1]
        for (int j = 0; j < n - i - 1; j++) {
            if (nums[j] > nums[j + 1]) {
                // 交换 nums[j] 与 nums[j + 1]
                int temp = nums[j];
                nums[j] = nums[j + 1];
                nums[j + 1] = temp;
                swapped = true; // 记录发生了元素交换
            }
        }

        // 如果没有发生交换，则说明数组已经有序，直接跳出循环
        if (!swapped) {
            break;
        }
    }
}

六、冒泡排序的特性

冒泡排序是一种简单的排序算法，它重复地遍历要排序的列表，通过比较相邻元素并交换它们，使得每一轮遍历都能找到当前未排序部分的最大值（或最小值），从而逐步将其放到正确的位置上。冒泡排序的特性包括：

1. 稳定性：冒泡排序是一种稳定的排序算法，即相同元素的相对位置在排序前后不会改变。
2. 时间复杂度：在最坏情况下，冒泡排序的时间复杂度为 $O(n^2)$，其中 $n$ 是要排序的元素个数。在最好情况下（即已经有序），时间复杂度为 $O(n)$。平均情况下的时间复杂度也为 $O(n^2)$。
3. 空间复杂度：冒泡排序的空间复杂度为 $O(1)$，因为它仅使用了常数级别的额外空间。
4. 原地排序：冒泡排序是一种原地排序算法，它只需要常数级别的辅助空间来存储临时变量，而不需要额外的数据结构。
5. 适用情况：由于冒泡排序的时间复杂度较高，通常不适用于大规模数据的排序，但在某些特定情况下（如数据基本有序的情况下），冒泡排序可能表现良好。

推荐阅读

1. Spring 三级缓存
2. 深入了解 MyBatis 插件：定制化你的持久层框架
3. Zookeeper 注册中心：单机部署
4. 【JavaScript】探索 JavaScript 中的解构赋值
5. 深入理解 JavaScript 中的 Promise、async 和 await