文章目录
- 1 特征工程
- 2 特征选择
- 3 相关性分析
- 3.1 皮尔逊相关系数
- 3.2 皮尔逊相关系数 - python实现
- 3.3 JS散度
- 3.4 JS散度 - python实现
- 4 模型解释算法
- 4.1 SHAP
- 4.2 SHAP - python实现
- 4.3 SHAP值解读
- 4.4 SHAP 瀑布图
- 4.5 SHAP 柱状图
- 4.6 SHAP 蜂巢图
- 4.7 SHAP其他图像形式
- 4.7.1 单点力图
- 4.7.2 多点力图
- 4.7.3 散点图
1 特征工程
维基百科中给特征工程做出了简单定义:特征工程是利用数据领域的相关知识来创建能够使机器学习算法达到最佳性能的特征的过程
Feature Engineering is the process of transforming raw data into features that better represent the underlying problem to the predictive models,resulting in improved model accuracy on unseen data.
简而言之,特征工程就是一个把原始数据转变成特征的过程,这些特征可以很好的描述这些数据,并且利用它们建立的模型在未知数据上的表现性能可以达到最优(或者接近最佳性能)
特征工程包括数据采集、数据清洗、特征提取、缺失值处理、数据变换、数据编码、无量纲处理、特征选择、降维等一系列步骤
2 特征选择
传统的特征工程进行到特征选择这一步骤,基本上需要对已有业务相关数据进行目标因变量相关性分析;
我们可以在训练模型前对自变量和因变量进行相关性分析,也可以对较多的模型进行降维处理;
或者在训练模型后利用模型的可解释性对变量的贡献程度进行论证
在本文中,我们重点介绍两个相关性分析方法和模型解释算法
关于降维的方法,在这篇博文中已有较为详细的解释和代码示例:KNN及降维预处理方法LDA|PCA|MDS
3 相关性分析
3.1 皮尔逊相关系数
在使用皮尔逊相关系数时我们需要注意他的基本假设,该系数只能判断自变量和因变量之间是否存在线性关系:
ρ X , Y = E [ ( X − μ X ) ( Y − μ Y ) ) ] σ X σ Y \rho_{X,Y} = \frac{E\big[(X-\mu_{X})(Y-\mu_{Y}))\big]}{\sigma_{X} \sigma_{Y}} ρX,Y=σXσYE[(X−μX)(Y−μY))]
皮尔逊相关系数
ρ
X
,
Y
\rho_{X,Y}
ρX,Y的取值范围在
(
−
1
,
1
)
(-1,1)
(−1,1)之间,0代表二者没有线性关系,越接近于0表示线性关系越弱;
+1或越接近+1代表二者呈现越强的正向线性关系,反之则是负向线性关系
3.2 皮尔逊相关系数 - python实现
scipy.stats 包的 pearsonr函数能够提供计算相关系数的功能
该函数同时会对皮尔逊相关系数做
H
0
H_0
H0为:二者为随机分布的假设检验,
当p值极小时,我们选择拒绝原假设,进而认同二者具有线性关系
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from scipy.stats import pearsonr
X, y = load_iris(return_X_y=True)
coef, p_value = pearsonr(X[:,0], y)
print(f"1st attribute's \npearson correlation: {coef}, p: {p_value}")
coef, p_value = pearsonr(X[:,1], y)
print(f"2nd attribute's \npearson correlation: {coef}, p: {p_value}")
coef, p_value = pearsonr(X[:,2], y)
print(f"3rd attribute's \npearson correlation: {coef}, p: {p_value}")
$ 1st attribute's
$ pearson correlation: 0.7825612318100811, p: 2.890478352614215e-32
$ 2nd attribute's
$ pearson correlation: -0.4266575607811239, p: 5.201563255177591e-08
$ 3rd attribute's
$ pearson correlation: 0.949034699008389, p: 4.201873152959405e-76
3.3 JS散度
JS散度来源于KL散度,后者是判断两个分布距离的一个数学公式
KL散度的计算公式如下:
K L [ P ( x ) ∣ ∣ Q ( x ) ] = ∑ x ∈ X [ P ( x ) l o g P ( x ) Q ( x ) ] KL[P(x)||Q(x)] = \displaystyle{\sum_{x \in X}[P(x)log\frac{P(x)}{Q(x)}]} KL[P(x)∣∣Q(x)]=x∈X∑[P(x)logQ(x)P(x)]
由于KL散度不具备对称性,因此后续提出JS散度,其公式即为KL散度的叠加:
J S [ P 1 ( x ) ∣ ∣ P 2 ( x ) ] = 1 2 K L [ P 1 ( x ) ∣ ∣ P 1 ( x ) + P 2 ( x ) 2 ] + K L [ P 2 ( x ) ∣ ∣ P 1 ( x ) + P 2 ( x ) 2 ] JS[P_1(x)||P_2(x)] = \frac{1}{2}KL[P_1(x)||\frac{P_1(x)+P_2(x)}{2}] + KL[P_2(x)||\frac{P_1(x)+P_2(x)}{2}] JS[P1(x)∣∣P2(x)]=21KL[P1(x)∣∣2P1(x)+P2(x)]+KL[P2(x)∣∣2P1(x)+P2(x)]
由定义可知,JS散度的取值范围是
[
0
,
1
]
[0,1]
[0,1];如果两个分布足够近,其二者JS散度将无限接近于0,这就意味着二者具备极强的相关性;
那么判断指标相关性时,我们可以取遍自变量和因变量的分布对,最后留下与因变量相关性最强的自变量
3.4 JS散度 - python实现
在scipy.stats 模块中,entropy函数能够直接求解两个分布KL散度的值,
然后我们可以根据JS散度的计算公式完成JS散度的计算
entropy方法的介绍如下:
scipy.stats.entropy(pk, qk=None, base=None, axis=0)
Calculate the entropy of a distribution for given probability values.
If only probabilities pk are given, the entropy is calculated as S = -sum(pk * log(pk), axis=axis).
If qk is not None, then compute the Kullback-Leibler divergence S = sum(pk * log(pk / qk), axis=axis).
This routine will normalize pk and qk if they don’t sum to 1.
注意,entropy方法的输入必须是两个分布,因此我们需要对原始数据做归一化处理,使其成为一个分布
但如果输入不是分布,该方法也会自动调成为分布进行计算
import scipy.stats as ss
import numpy as np
from scipy.stats import entropy
from sklearn.datasets import load_iris
iris_x, iris_y = load_iris(return_X_y=True)
def js_divergence(p,q):
p = np.array(p)
q = np.array(q)
M = (p+q)/2
js = 0.5*entropy(p,M) + 0.5*entropy(q,M)
return np.round(float(js),6)
attr_1 = iris_x[:,0]
attr_2 = iris_x[:,1]
attr_3 = iris_x[:,2]
attr_4 = iris_x[:,3]
res1 = js_divergence(attr_1,iris_y)
res2 = js_divergence(attr_2,iris_y)
res3 = js_divergence(attr_3,iris_y)
res4 = js_divergence(attr_4,iris_y)
print("js divergance: attr1:{}, attr2:{}, \
arrt3:{}, attr4:{}" \
.format(res1,res2,res3,res4))
$ js divergance:
$ attr1:0.157331,
$ attr2:0.18844,
$ arrt3:0.064379,
$ attr4:0.028869
4 模型解释算法
4.1 SHAP
SHAP在机器学习领域中被用来直观表示多元回归或分类模型中各属性变量对因变量变化的贡献程度;
由于多数树型机器学习模型常常具备极低的可解释性,SHAP方法能够很直观的呈现出各自变量对于目标因变量的重要程度
SHAP算法直接来源于博弈论中的一种解决方案,是一种在玩家中公平分配支出的数学方法,该种算法在博弈轮中计算的指标是Shapley值
简单来说,假设这样一种情形:多名玩家组成任务联盟共同协作完成一项任务,并获得相应的奖励;
在完成任务的过程中,任务中玩家的数量和玩家进入任务的顺序都会直接影响任务的奖励数值
此时,我们需要通过已知的玩家序列及对应的奖励数值推断出:
某一个玩家的加入能够为任务带来附加奖励的数值,这就是该名玩家对于当前任务联盟的边际贡献值
某名玩家的Shapley值便是该名玩家加入所有可能任务联盟组合后贡献的边际贡献值加权求和,公式为:
ϕ i = ∑ S ⊆ N ∖ { i } ∣ S ∣ ! ( N − ∣ S ∣ − 1 ) ! N ! [ v ( S ∪ { i } ) − v ( S ) ] \phi_i = \displaystyle{\sum_{S \subseteq N\setminus\{i\}}\frac{|S|!(N-|S|-1)!}{N!}\big[v(S\cup\{i\})-v(S)\big]} ϕi=S⊆N∖{i}∑N!∣S∣!(N−∣S∣−1)![v(S∪{i})−v(S)]
在以上公式中,
ϕ
i
\phi_i
ϕi是第i位玩家的shapley值,
S
S
S是第i位玩家加入前任务联盟集合(该集合是有序的),
N
N
N是所有参加任务的任务集合
v
(
S
∪
{
i
}
)
−
v
(
S
)
v(S\cup\{i\})-v(S)
v(S∪{i})−v(S)表示第i位玩家加入后对任务联盟
S
S
S带来的边际贡献
v
(
S
)
v(S)
v(S)就是
S
S
S特征联盟下的价值函数值
∑
S
⊆
N
∖
{
i
}
\sum_{S \subseteq N\setminus\{i\}}
∑S⊆N∖{i}代表对所有可能的任务联盟求和,
∣
S
∣
!
(
N
−
∣
S
∣
−
1
)
!
N
!
\frac{|S|!(N-|S|-1)!}{N!}
N!∣S∣!(N−∣S∣−1)!是权值
举例而言,
{
A
,
B
,
C
}
\{A,B,C\}
{A,B,C}三人之中的某几个人或者是全部来完成任务,A单独完成能够获得10奖励;
此时如果B加入,奖励变为15,此时在这个情形下B对
{
A
,
B
}
\{A,B\}
{A,B}任务联盟的边际贡献值就是
15
−
10
=
5
15-10=5
15−10=5
但以上只是一种B加入联盟的情况,我们需要穷尽
{
A
,
C
}
\{A,C\}
{A,C}所有可能的任务联盟组合,然后计算B加入后所产生的边际贡献值,最后使用公式计算B的Shapley值
将Shapley值移植到机器学习中,从概念上来说是非常自然的,机器学习算法中的各种属性即可以视为shapley博弈决策模型中的每一名玩家
唯一不同的地方在于,当我们计算某个属性的边际贡献值时,在选中属性联盟后,剩余的属性我们仍旧需要关注,因为所有的属性共同决定了回归值或者是分类值的计算
因此,计算某个属性边际贡献的公式需要这样进行迁移和改写:
v f , x ( i ) ( S ) = ∫ f ( x S ( i ) ∪ X C ) d P X C − E [ f ( X ) ] v_{f,x^{(i)}}(S) = \int f(x_{S}^{(i)} \cup X_C)d\mathbb{P}_{X_C} - \mathbb{E}[f(X)] vf,x(i)(S)=∫f(xS(i)∪XC)dPXC−E[f(X)]
在以上公式中,我们认为所有属性服从一个联合超分布,
v
f
,
x
(
i
)
(
S
)
v_{f,x^{(i)}}(S)
vf,x(i)(S)即表示在
f
f
f这个超分布下,第i个数据点在特征联盟
S
S
S之下的价值函数
而
X
C
X_C
XC即表示不在特征联盟中所有属性的具体取值,
∫
f
(
x
S
(
i
)
∪
X
C
)
d
P
X
C
\int f(x_{S}^{(i)} \cup X_C)d\mathbb{P}_{X_C}
∫f(xS(i)∪XC)dPXC 即对不在特征联盟中的属性进行积分,这样能够穷尽所有不在特征联盟中属性的各种取值
最后,我们人为减去预测值的期望
E
[
f
(
X
)
]
\mathbb{E}[f(X)]
E[f(X)],这代表所有数据点依据模型预测出来预测值的平均值
综上,我们可以求得边际贡献值为:
v ( S ∪ j ) − v ( S ) = ∫ f ( x S ( i ) ∪ X C ∖ j ) P X C ∖ j − ∫ f ( x S ( i ) ∪ X C ) P X C v(S\cup j) - v(S) = \int f(x_{S}^{(i)} \cup X_{C\setminus j})\mathbb{P}_{X_{C\setminus j}} - \int f(x_{S}^{(i)} \cup X_C)\mathbb{P}_{X_C} v(S∪j)−v(S)=∫f(xS(i)∪XC∖j)PXC∖j−∫f(xS(i)∪XC)PXC
根据边际贡献值,我们可以轻松求出某一个属性下某一个数据点的SHAP值:
ϕ j ( i ) = ∑ S ⊆ { 1 , 2 , ⋯ , p } ∖ j ∣ S ∣ ! ( p − ∣ S ∣ − 1 ) ! p ! ( ∫ f ( x S ( i ) ∪ X C ∖ j ) P X C ∖ j − ∫ f ( x S ( i ) ∪ X C ) P X C ) \phi_j^{(i)} = \displaystyle{\sum_{S \subseteq \{1,2,\cdots,p\} \setminus j}\frac{|S|!(p-|S|-1)!}{p!}}\big(\int f(x_{S}^{(i)} \cup X_{C\setminus j})\mathbb{P}_{X_{C\setminus j}} - \int f(x_{S}^{(i)} \cup X_C)\mathbb{P}_{X_C}\big) ϕj(i)=S⊆{1,2,⋯,p}∖j∑p!∣S∣!(p−∣S∣−1)!(∫f(xS(i)∪XC∖j)PXC∖j−∫f(xS(i)∪XC)PXC)
其中,
p
p
p 代表属性数量,剩余部分我们已经在Shapley公式中有过表述,求加权平均的思想在这里是没有变化的
为了能够更直观的理解SHAP公式,我们假设目标函数是各个属性线性加合的情况,在线性模型中,由于不存在交叉项,各个属性之间的预测值是相互独立的,也就是说,超参数分布仅仅是各个属性分布之间的简单相乘:
f ( x ) = β 0 + β 1 x 1 + β 2 x 2 + ⋯ + β p x p f(x) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_p x_p f(x)=β0+β1x1+β2x2+⋯+βpxp
此时,我们可以很轻松的定义第i个样本第j个特征的边际贡献值为:
ϕ j ( i ) = β j x i − E ( β j x i ) = β j x i − β j E ( x i ) \phi_j^{(i)} = \beta_j x_i - E(\beta_j x_i) = \beta_j x_i - \beta_jE( x_i) ϕj(i)=βjxi−E(βjxi)=βjxi−βjE(xi)
那么,将该样本所有特征值的边际贡献相加,我们可以得到一个非常有用的结论:
∑ j = 1 p ϕ j ( f ) = ∑ j = 1 p β j x i − E ( β j x i ) = f ( x i ) − E [ f ( X ) ] \begin{array}{ll} \displaystyle{\sum_{j=1}^{p}\phi_j(f)} & = & \displaystyle{\sum_{j=1}^{p}\beta_j x_i - E(\beta_j x_i)}\\ & = & f(x_i) - E[f(X)] \end{array} j=1∑pϕj(f)==j=1∑pβjxi−E(βjxi)f(xi)−E[f(X)]
也就是说样本
x
i
x_i
xi的所有特征的贡献之和等于该样本的预测值减去所有样本的平均预测值
当然,对于更复杂的回归或是分类模型来说,超分布的计算是十分困难的,因此我们常规使用的SHAP算法在计算过程中进行了很多优化, 这里我们就不再介绍
4.2 SHAP - python实现
我们可以通过下载安装 shap 包来使用shap模型的全部功能
为了能够使用shap算法计算模型中各属性的贡献度,我们在示例中选用xgboost随机森林进行模型训练
shap模型的数据结果和图像解读是非常关键的,在接下来的栏目中我们将逐一重点分析
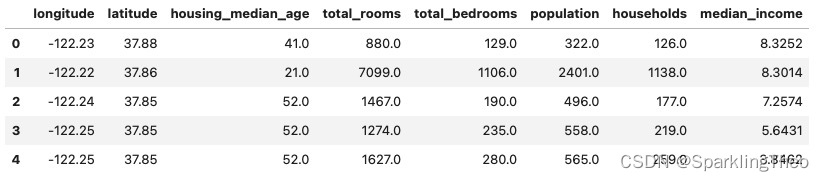
示例中数据选用的是sklearn.datasets中加利福尼亚房价数据,我们将用SHAP算法检测一个回归模型
import numpy as np
import warnings
from sklearn.datasets import fetch_openml
warnings.filterwarnings("ignore")
X, y = fetch_openml('california_housing',version=1,as_frame=True, return_X_y=True)
X.drop("ocean_proximity",axis=1,inplace=True)
X.fillna(0,inplace=True)
X.head(5)
import xgboost
import shap
rf_reg = xgboost.XGBRegressor(random_state=42)
rf_reg.fit(X,y)
explainer = shap.Explainer(rf_reg)
shap_values = explainer(X)
4.3 SHAP值解读
Explainer将会分别输出每一个数据点的相应数据,因此该输出矩阵的行维度将与输入数据的维度相同
接下来,我们需要重点解读输出矩阵的三个列维度
- base_values是我们在理论中介绍的所有数据点所有属性在模型中预测的均值,即
E
[
f
(
X
)
]
E[f(X)]
E[f(X)]
- values是每一个属性在该数据点上使用模型预测的值,即
f
(
x
i
)
f(x_i)
f(xi)
- data则是该数据点在每个属性上的输入值
接下来,我们无论使用什么图像来可视化SHAP值,本质上都是在使用这三组数据
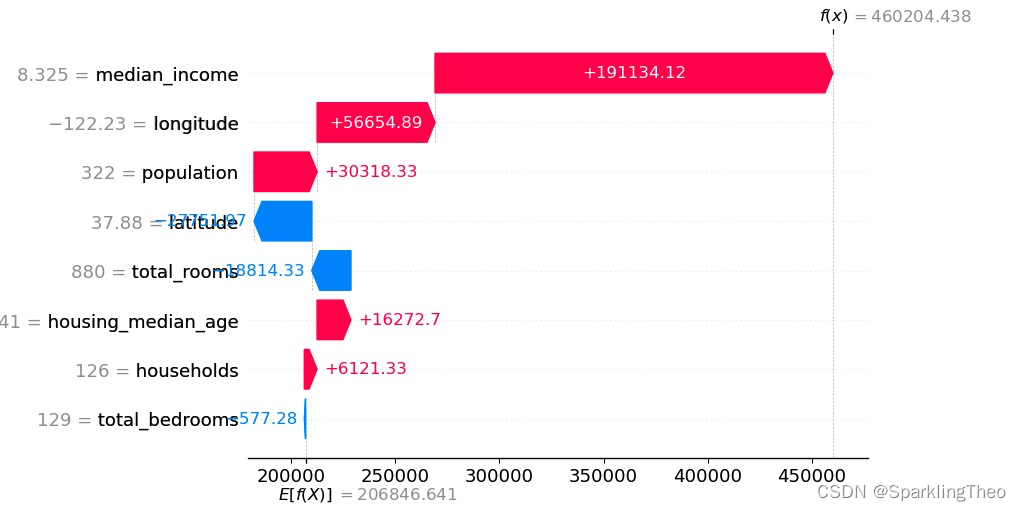
shap_values[0]
$.values =
array([ 56654.895 , -27751.975 , 16272.704 , -18814.334 , -577.2811,
30318.332 , 6121.3276, 191134.12 ], dtype=float32)
$ .base_values =
206846.64
$ .data =
array([-122.23 , 37.88 , 41. , 880. , 129. , 322. ,
126. , 8.3252])
4.4 SHAP 瀑布图
瀑布图用于展现某一个数据点各个属性对于最终预测值的贡献程度
具体而言,每一个属性在该数据点上都会存在该点该属性预测值与所有数据点所有属性预测均值的差值
我们观察两个重要的数据,一个是右上角的
f
(
x
)
f(x)
f(x),另外一个是左下角的
E
[
f
(
x
)
]
E[f(x)]
E[f(x)],
瀑布图中所有数据值和即为
f
(
x
)
f(x)
f(x)【数据点预测值】与
E
[
f
(
x
)
]
E[f(x)]
E[f(x)]【整体预测均值】的差值,这就代表了每一个属性对于该数据点回归值的贡献程度
最后,红色表示做正向贡献,蓝色表示做负向贡献
shap.plots.waterfall(shap_values[0])
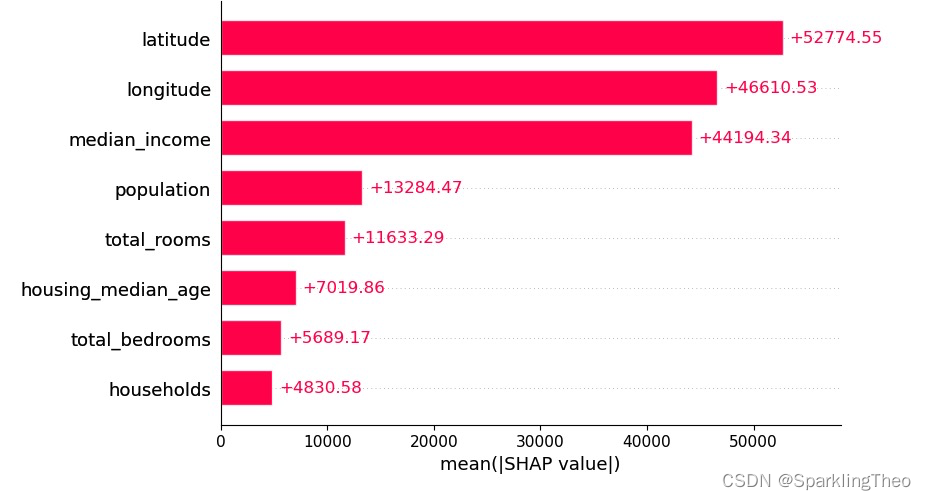
4.5 SHAP 柱状图
柱状图将计算所有数据点各个属性贡献的平均值,因此我们将看到聚合统计量
从数据呈现的角度分析,SHAP均值越大的属性平均贡献越大
注意,SHAP算法在进行计算之前均对数据进行了log归一化处理,因此贡献度不会受数据量纲影响
shap.plots.bar(shap_values,max_display=10)
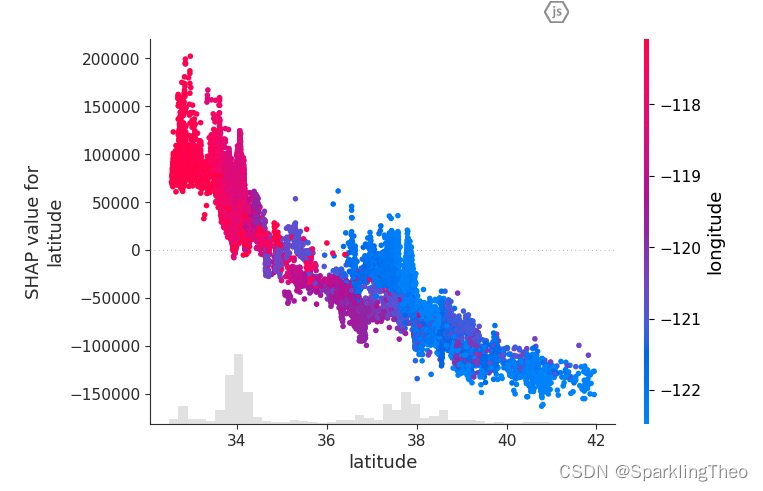
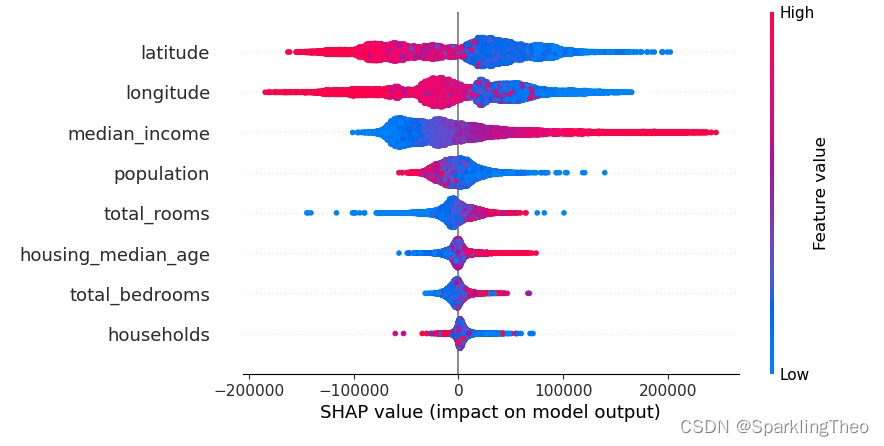
4.6 SHAP 蜂巢图
蜂巢图也是最为重要的一种可视化方式。首先我们要知道蜂巢图实际上一个伪3D图像
图中每一个点代表一个数据点,颜色代表的是数据点在该属性下的具体值,只是被模糊处理了
横坐标即为该数据点在该属性下(纵坐标表示)的SHAP值
读图时,高SHAP值和高Feature Value值意味着该属性对回归值有更积极的正面贡献,
反之,高SHAP和低Feature Value值则意味着该属性对回归值有更强烈的负面贡献
以下图为列,latitude属性对预测回归值有较强的负面贡献,因为高SHAP值的区间都是蓝色的数据点;
而与之相对的,median_income属性则对预测回归值有很强的正面贡献,由于高SHAP值的区间都是红色的数据点;
shap.plots.beeswarm(shap_values)
4.7 SHAP其他图像形式
只要掌握三个基础的数值,剩下的可视化图像是很好理解的,下面不加阐释低列举出SHAP包提供的其他可视化图像
4.7.1 单点力图
# 力图 - 全部属性的单点图
shap.initjs()
shap.force_plot(shap_values[0])

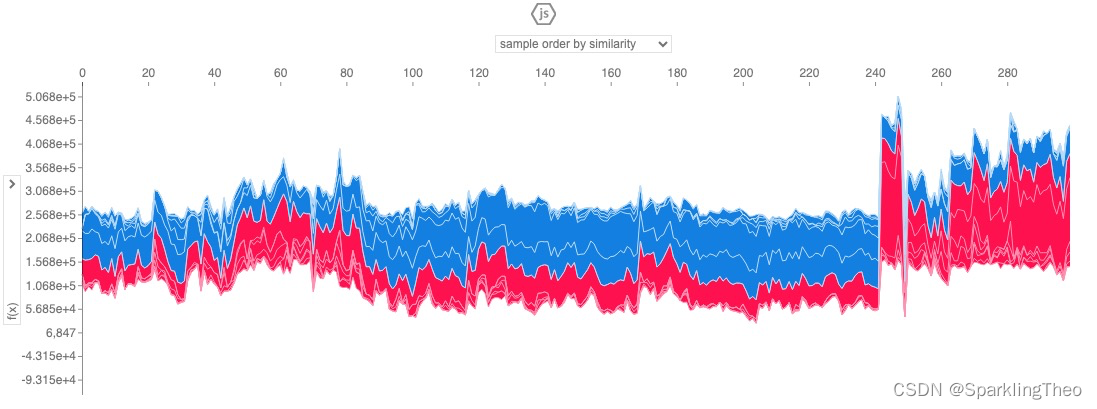
4.7.2 多点力图
# 力图 - 全部属性的多点图
shap.initjs()
shap.plots.force(shap_values[:300])
4.7.3 散点图
# 散点图 - 某个属性的多点图
shap.initjs()
shap.plots.scatter(shap_values[:, "latitude"], color=shap_values)