题目描述：

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

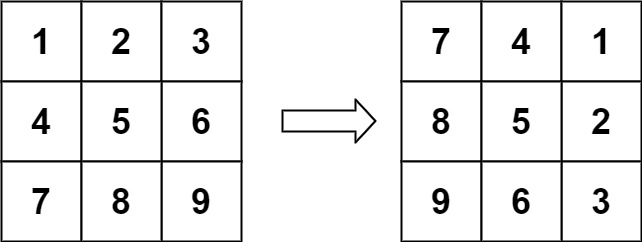
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

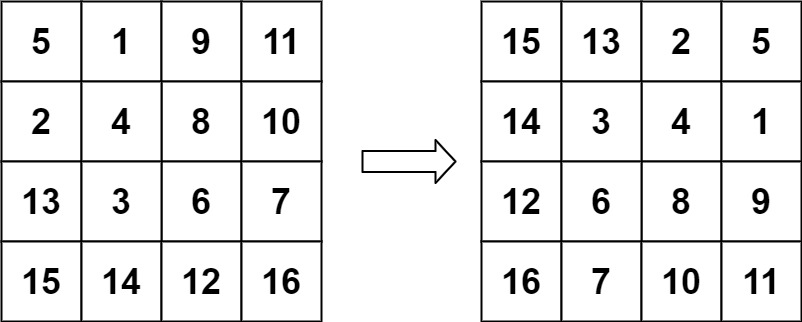
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 20
• -1000 <= matrix[i][j] <= 1000

题解1：

最原始的做法，通过对每一行进行旋转进行找规律，发现有如下的公式：

 matrix[j][n - 1 - i] = matrix[i][j];

但是如果直接通过遍历数组来进行该公示的应用，那么之前已经置换过的位置会影响没有置换过的位置，因此还需要将原始数组保存起来，进行置换的时候 就将辅助数组的元素放置在原始数组的对应位置，这样就避免了原始数组被覆盖的可能。

代码实现：

public static void rotate(int[][] matrix) {
        int n = matrix.length;
        int[][] tmp = new int[n][];
        for (int i = 0; i < n; i++) {
            tmp[i] = matrix[i].clone();
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                matrix[j][n-i-1] = tmp[i][j];
            }
        }
    }

知识点：

1、二维数组一整行进行拷贝复制：

tmp[i] = matrix[i].clone(); 

这样做的的问题：空间复杂度很大，考虑是否可以实现原地反转，即就在当前数组上进行翻转。

题解2 ：

通过尝试发现，如果每次只取前n/2行和(n+1)/2行的这一片元素进行旋转就不会产生原始没用放到正确位置上的元素被覆盖的情况，比如说，现在就取四个角，        A B

                                                                                                         C D

旋转之后，A->B  B->D  D->C  C->A，实现的时候逆着来，即先重置A位置为C，再重置C位置为D，以此类推，但是需要先保存A位置的初始值，这样才能将B位置置为A。这样实现的旋转是不会产生元素覆盖的。

代码实现：

public static void rotate2(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n/2; i++) {
            for (int j = 0; j < (n+1)/2; j++) {
                int tmp = matrix[i][j];
                matrix[i][j] = matrix[n-1-j][i];
                matrix[n-1-j][i] = matrix[n-1-i][n-1-j];
                matrix[n-i-1][n-1-j] = matrix[j][n-1-i];
                matrix[j][n-1-i] = tmp;
            }
        }
    }

反思：这样的想法是有考虑到的，但是由于不知道中间的元素要具体怎样旋转而没有深入思考， 其实如果能尝试写一下旋转公示的话，应该就能看出来其实中间的元素也和外围元素有一样的公式。但是取n/2和n+1/2进行旋转我也是想不到的，总结一下经验只能。