作者:@学习同学
专栏:@数据结构进阶
作者简介:大二学生 希望能和大家一起进步!
本篇博客简介:简单介绍高阶数据结构位图
位图的介绍
- bitset的介绍
- 位图的引入
- 位图的概念
- 位图的引用
- bitset的使用
- bitset定义方式
- 方式一 默认初始化
- 方式二 赋初值
- 方式三 字符串初始化
- bitset成员函数的使用
- set
- reset
- flip
- test
- count
- size
- any none all
- bitset运算符的使用
- 流插入 流提取运算符
- 赋值 单目 复合运算符
- 位运算符
- bitset中[ ]运算符的使用
bitset的介绍
位图的引入
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中?
对于无序的数组来说 我们这里可能会想到这么几种方法来查找里面的元素
- 直接遍历整个数组 时间复杂度O(N) 但是每找一次都要从头遍历一遍
- 排序后二分查找 排序的时间复杂度是O(N*Log(N)) 之后每次查找时间复杂度Log(N)
- 将所有数据插入到unordered_set中 插入时间复杂度O(N) 每次查找的时间复杂度O(1)
这些算法的效率看上去很不错 但是忽略了一种很重要的点
40亿个重复的无符号数 它占用的内存是16个G 从空间消耗来说 这是不被允许的
解决方案
我们在从这四十亿个数中找一个数存不存在实际上就是判断这个数的状态
而这个数的状态只可能是存在或者不存在两种 只需要通过二进制 1 0 就能表示这两种状态
所以说对于每个整数我们只需要计算机中的一个最小储存单位来记录就可以
如图
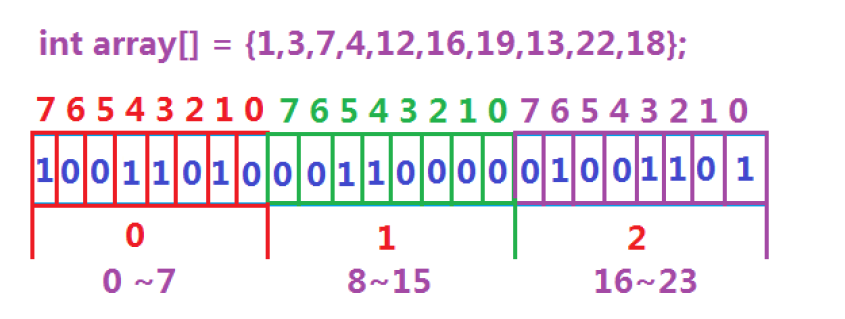
而本来需要四个字节的数据 现在我们使用一个bit位就解决了
所以说使用空闲缩小了 32倍 也就是500多mb
位图的概念
位图 就是用每一位来存放某种状态
它适用于海量数据 数据无重复的场景 通常是用来判断某个数据存不存在的
位图的引用
- 快速查找某个数据是否在一个集合中
- 排序
- 求两个集合的交集 并集等
- 操作系统中磁盘块标记
- 内核中信号标志位(信号屏蔽字和未决信号集)
bitset的使用
bitset定义方式
方式一 默认初始化
代码表示如下
bitset<16> bs1;
显示效果如下
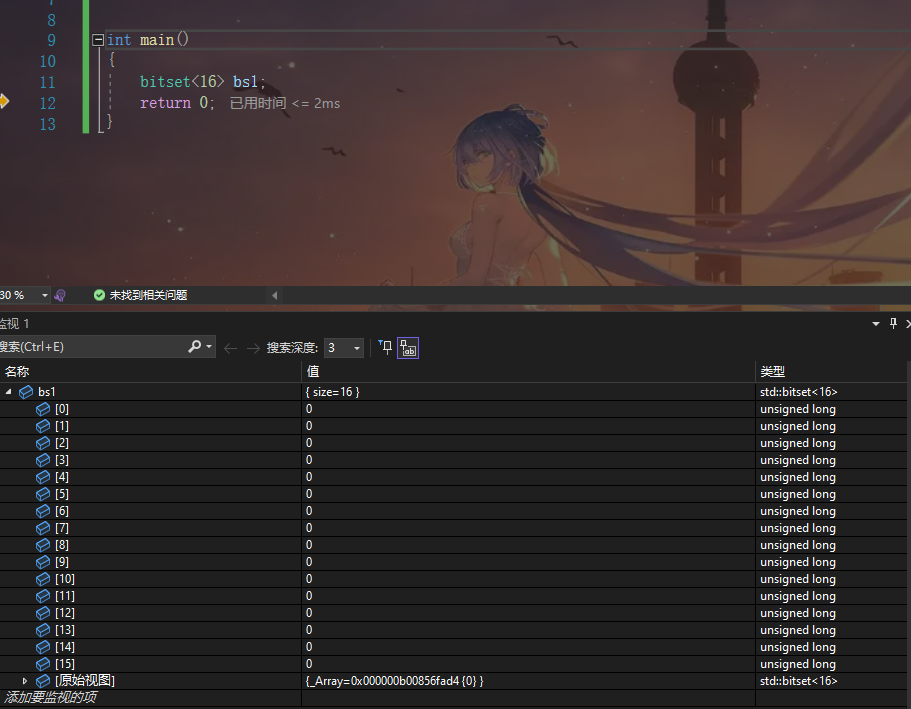
我们可以发现 所有的比特位都被初始化为0了
方式二 赋初值
代码表示如下
bitset<16> bs1(0xffff);
显示效果如下
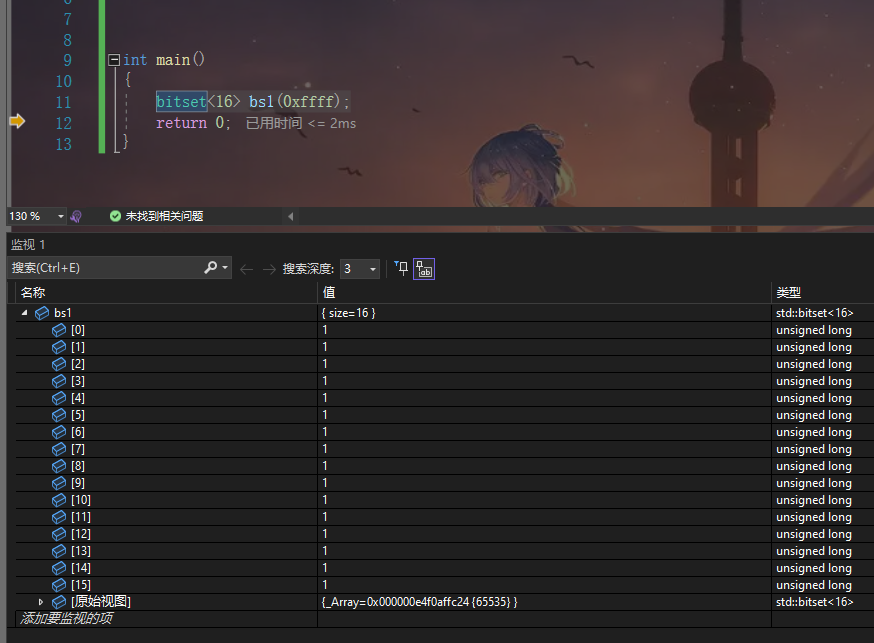
我们可以发现所有的bit位全部被初始化成1了 刚好符合0xffff
方式三 字符串初始化
代码表示如下
bitset<16> bs1(string("011011"));
显示效果如下
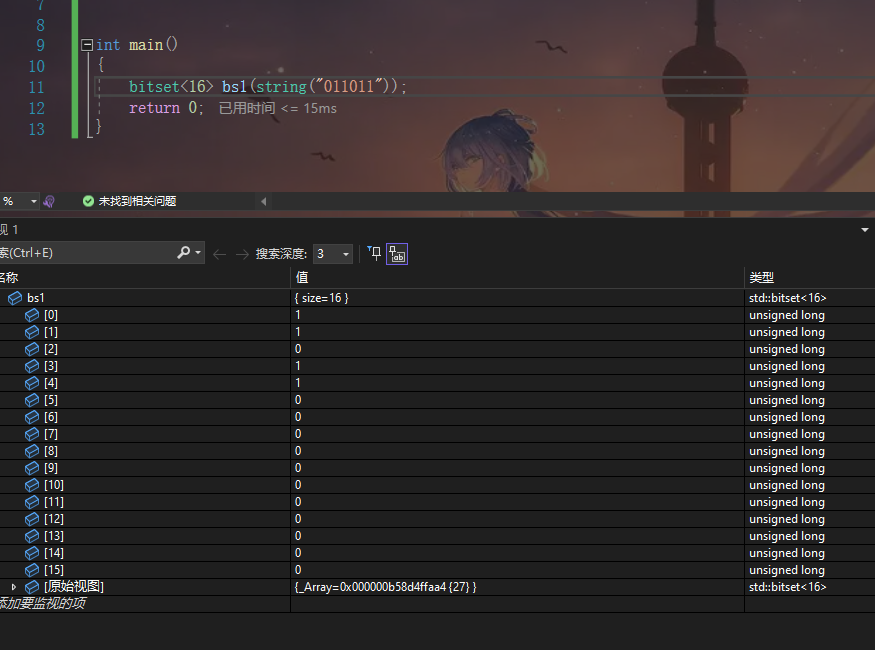
我们可以看到这个字符串匿名对象将前六个bit位初始化了
bitset成员函数的使用
bitset中常用的成员函数如下
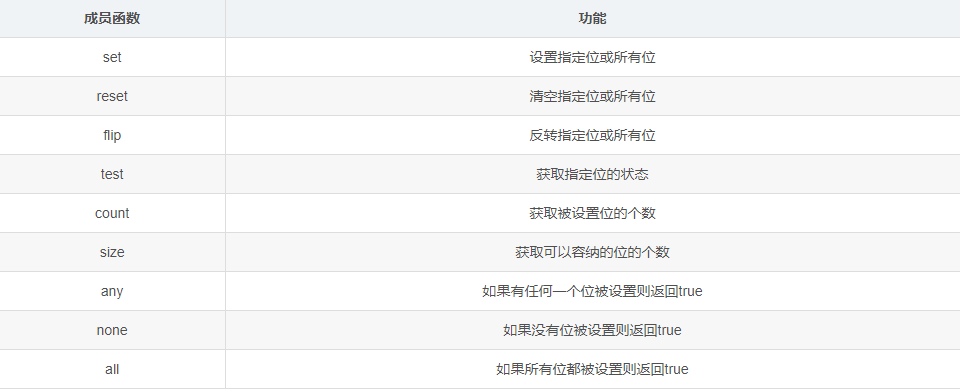
set
设置指定位置 若不指定设置位置则设置全部位
tip: 基本bitset的所有成员函数都是你如果不指定位置就设置整个容器 我们只在set中强调一遍 后序所有代码均指定位置
代码如下
bitset<8> bs;
bs.set();
显示效果如下
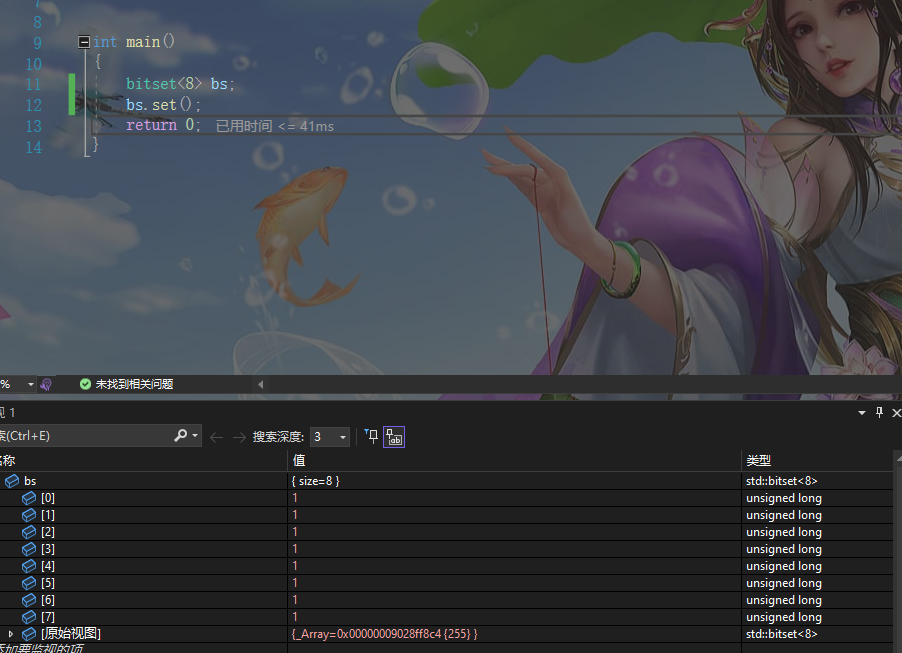
假设我们设置指定位置的话 代码如下 显示效果如下
bitset<8> bs;
bs.set(2);
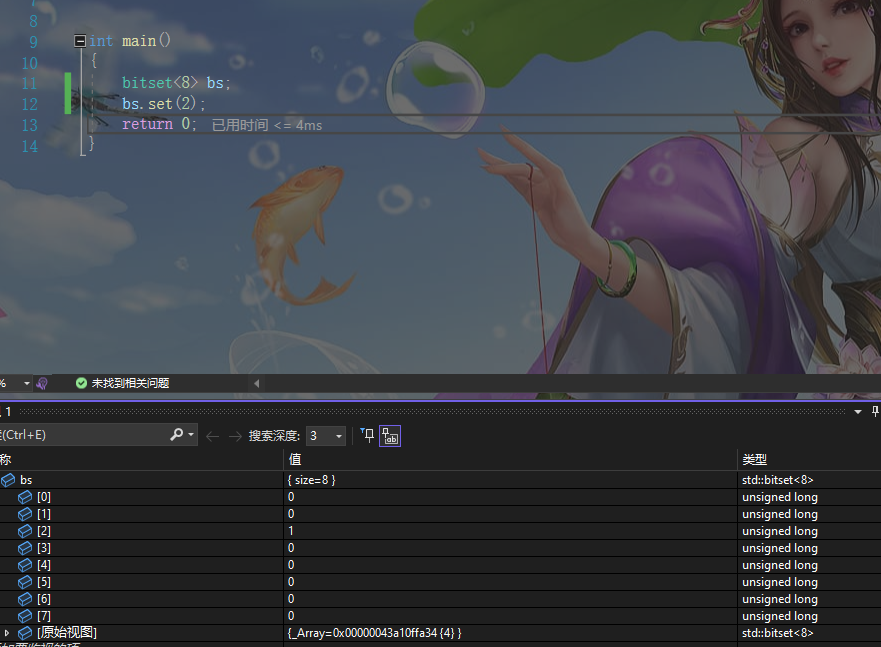
我们可以发现只有第二位被设置成了1
reset
清空指定位和所有位
代码和演示效果如下
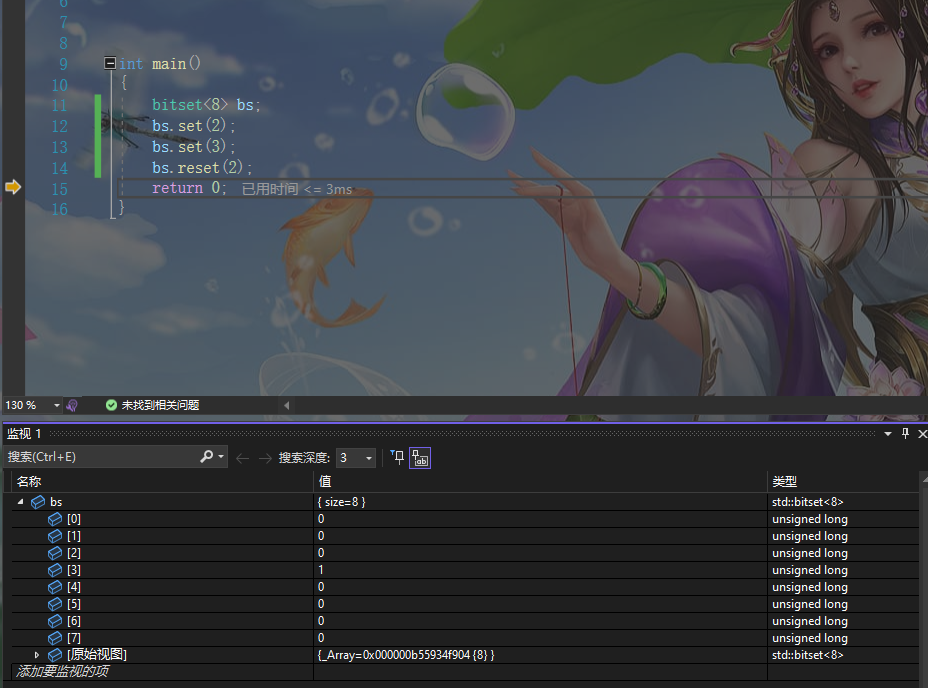
我们可以看到reset之后2的位置变成0了
flip
翻转指定或者是所有位
flip我们一般就是用来反转所有位置的 因为要反转单个位的话其实set和reset就够用了
代码和显示效果如下
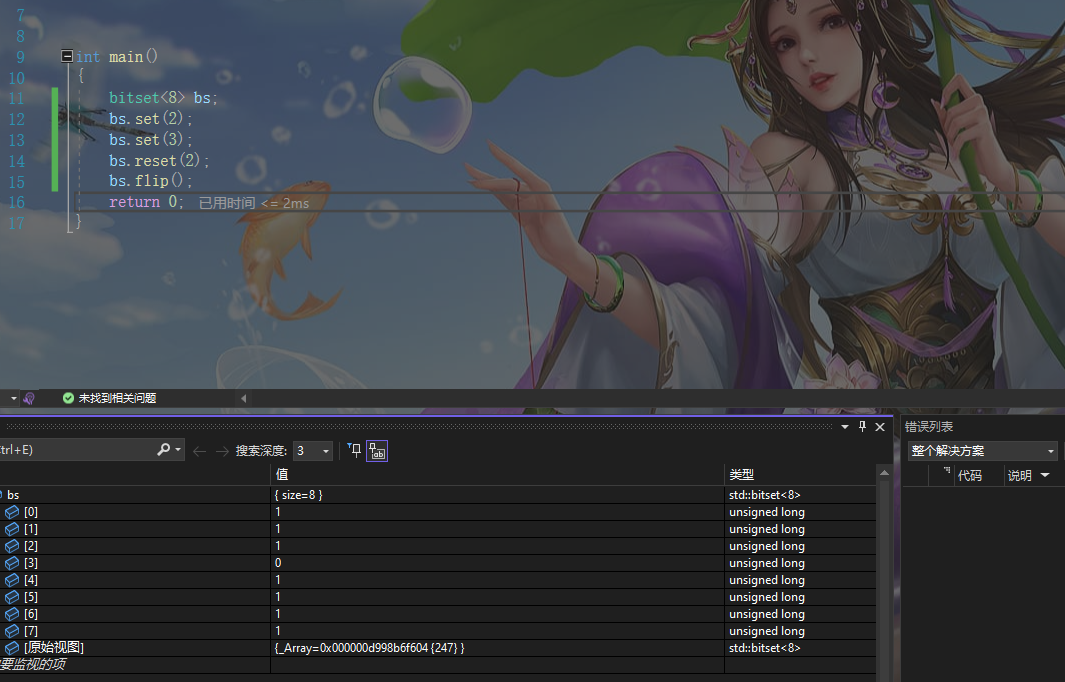
我们可以发现 全部位置都被反转了
test
获取指定位置的状态
我们用2和3来做测试 代码和演示效果如下
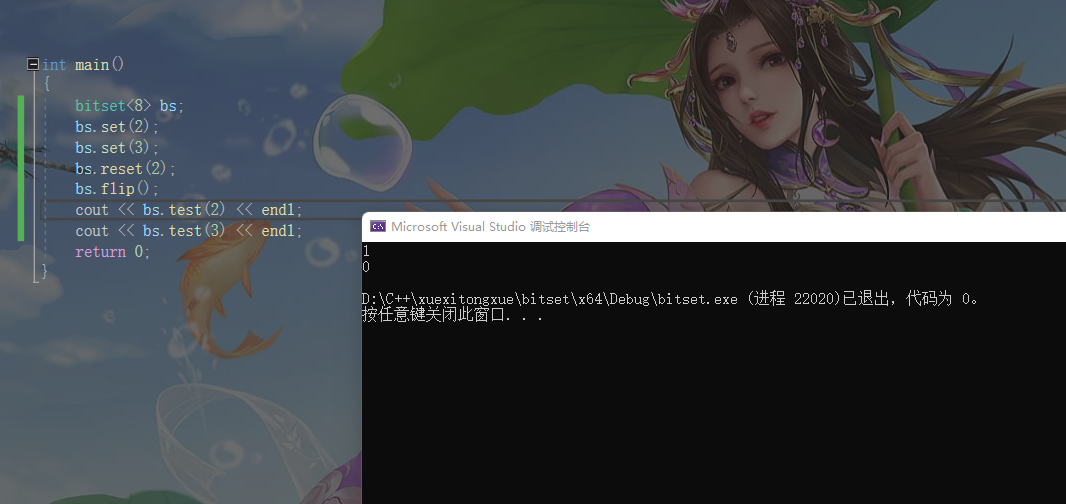
我们可以发现 和上面的测试结果相吻合
count
获取被设置的个数
代码和演示效果如下
bitset<8> bs;
bs.set(2);
bs.set(3);
bs.reset(2);
bs.flip();
cout << bs.count() << endl;
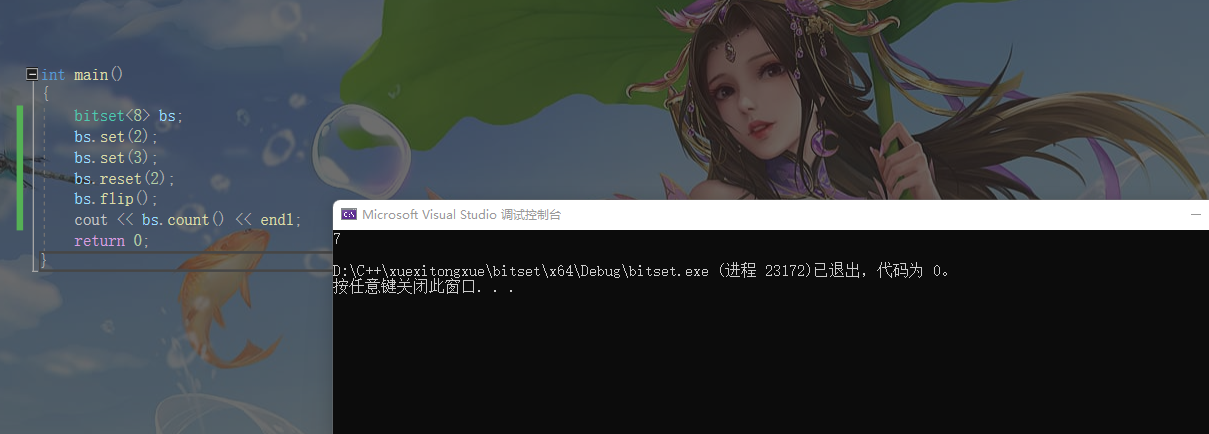
size
获取位图的大小 代码和演示结果表示如下
bitset<8> bs;
cout << bs.size() << endl;
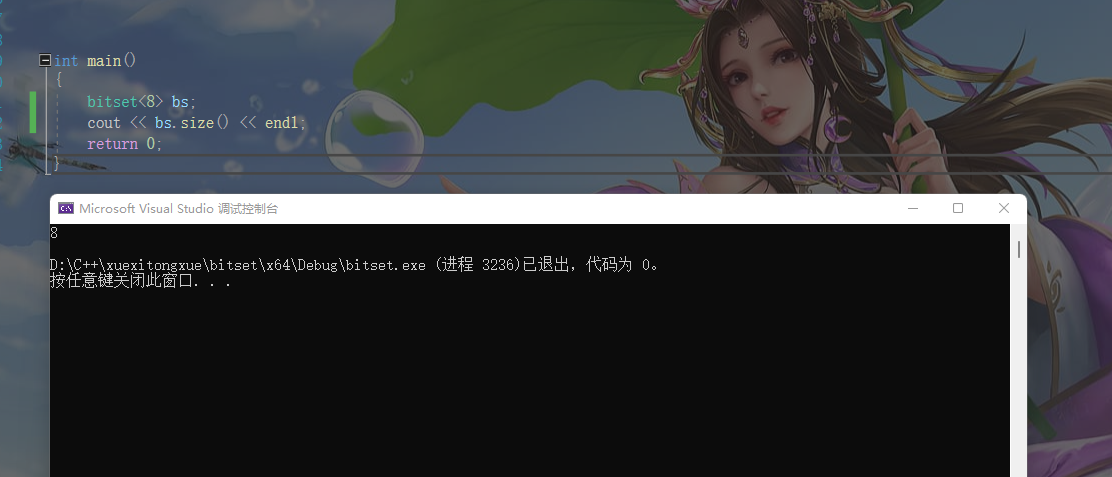
any none all
这三个结构函数的返回值都是bool类型 它们的含义分别是
- any 如果有值被设定就返回真
- none 如果没有值被设定就返回真
- all 如果所有值被设定就返回真
验证代码如下
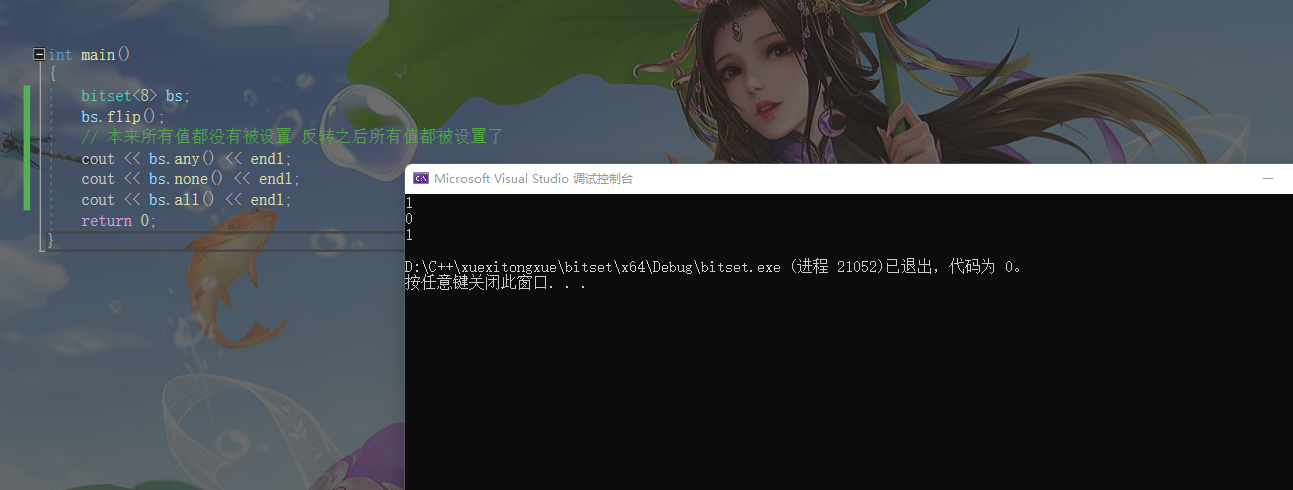
结果确实符合我们的预期
bitset运算符的使用
流插入 流提取运算符
bitset中重载了流插入和流提取运算符 演示代码如下
bitset<8> bs;
cin >> bs;
cout << bs << endl;
我们输入 010110 六个bit位
最后结果会变成这样子
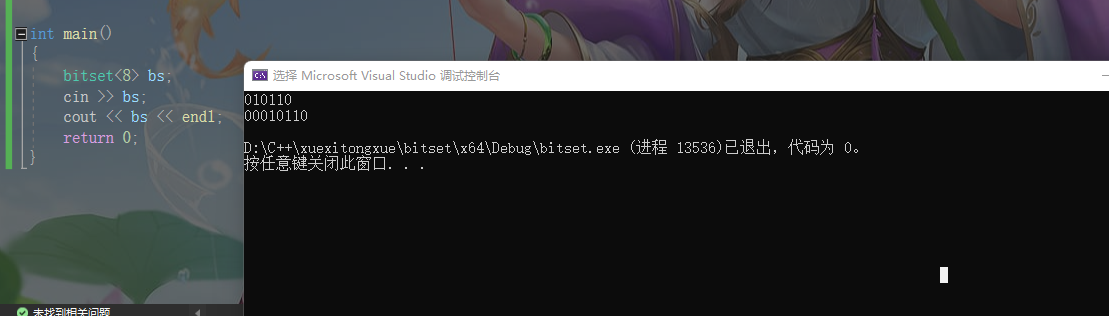
bs的低六位被重设了
赋值 单目 复合运算符
此外 bitset的操作符也被重载了很多
这些操作符大部分用法和原本意义类似 这里演示下它们的用法
bitset<8> bs(string("01010101"));
bs >>= 1;
cout << bs << endl;
cout << ~bs << endl;
演示结果如下
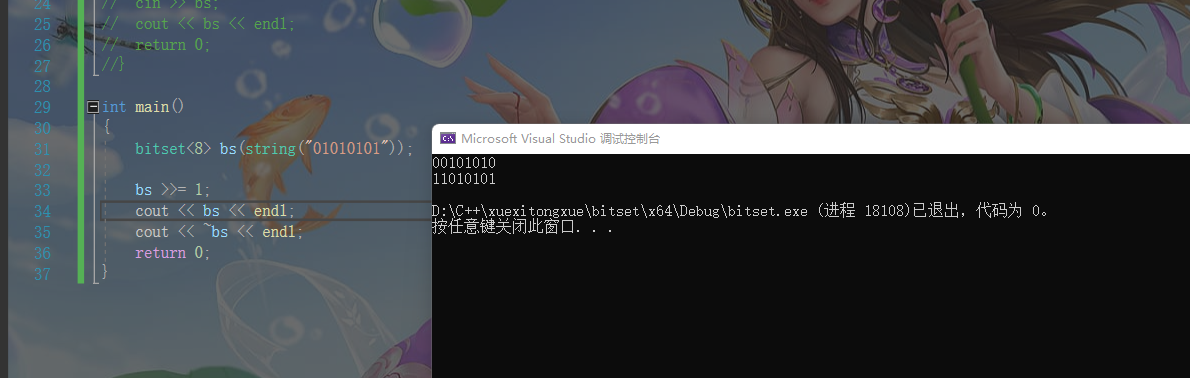
位运算符
同样的 bitset也对位运算符进行了重载
我们这里直接给出演示的代码和图
bitset<8> bs(string("01010101"));
bitset<8> bs2; // 0000 0000
cout << (bs | bs2) << endl;
cout << (bs & bs2) << endl;
cout << (bs ^ bs2) << endl;
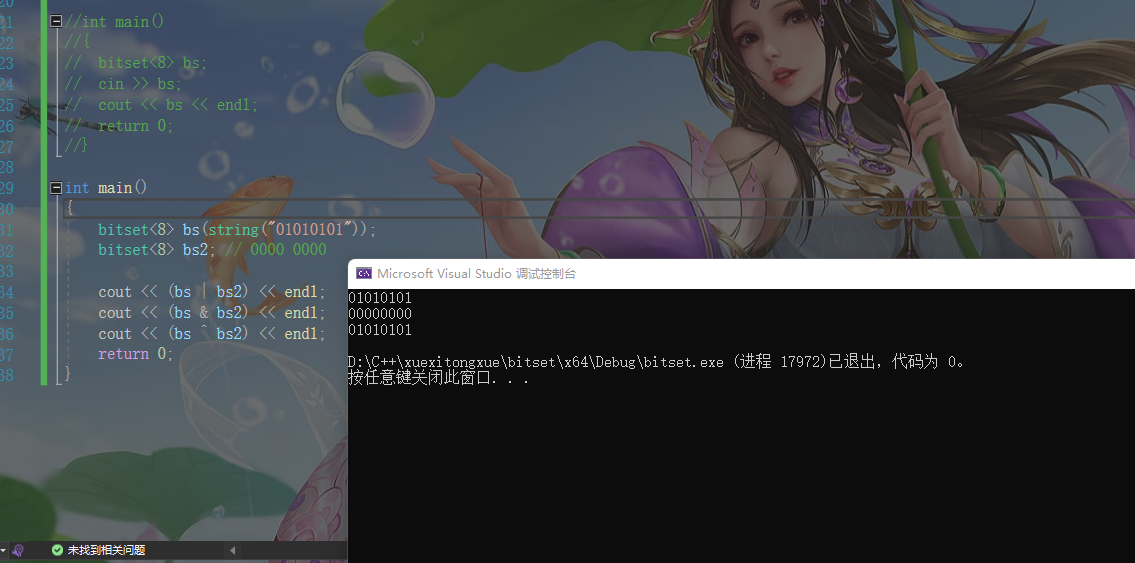
bitset中[ ]运算符的使用
同样的 bitset对于【】运算符也进行了重载 我们这里给出重载后的代码和效果
bitset<8> bs(string("11111111"));
bs[0] = 0;
cout << bs << endl;
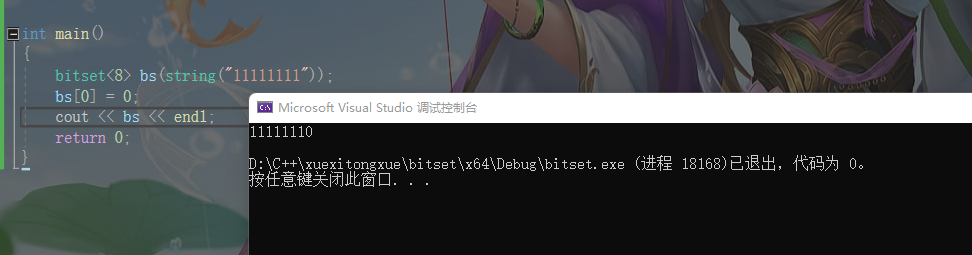
我们可以发现第0位被修改成0了