目录
一、数据结构的起源与发展
二、什么是数据结构
三、数据的逻辑结构和存储结构
四、数据类型和数据结构
五、算法
六、算法与数据结构的关系
七、算法时间复杂度和空间复杂度
一、数据结构的起源与发展
数据结构的起源可以追溯至1968年。当时,美国的唐·欧·克努特(Donald E. Knuth)教授在《计算机程序设计艺术》第一卷《基本算法》中系统阐述了数据的逻辑结构和存储结构及其操作,这标志着数据结构课程体系的开创。克努特教授的工作为数据结构的研究奠定了坚实的基础,并使得数据结构成为计算机科学中的一个重要分支。
发展历史:
- 无结构阶段:在20世纪40至60年代,计算机的应用主要集中在科学计算领域,数据之间的关系主要依赖于数学公式或模型。在这个阶段,数据结构的概念尚未明确形成,程序处理的大多是纯粹的数值数据。
- 结构化阶段:随着计算机在非数值处理领域的广泛应用,人们开始认识到程序设计规范化的重要性,并提出了程序结构模块化的概念。在这一阶段,数据结构及抽象数据类型逐渐形成,数据表示和操作的结构化成为了程序设计的重要问题。随着数据规模的加大,程序的设计越来越依赖于数据结构的设计。
- 面向对象阶段:从80年代初期开始,随着计算机技术的不断发展和普及,面向对象的程序设计方法逐渐被提出。在这个阶段,数据结构变得更加丰富,封装类的出现大大减少了程序设计者的负担,使得数据结构更加友好和易于使用。
此外,随着计算机科学的发展,数据结构也在不断演化和完善。线性结构(如数组、链表、栈和队列等)和非线性结构(如树和图等)先后被引入并广泛应用于各种计算场景中。同时,还出现了一些高级数据结构,如哈希表、堆、并查集等,这些数据结构在处理复杂问题和优化性能方面发挥了重要作用。
总的来说,数据结构的起源和发展历史是一个与计算机科学和技术进步紧密相连的过程。随着计算机应用的不断扩展和深化,数据结构也在不断发展和完善,为计算机科学的发展提供了重要的支撑和推动。
对于一个任务,解决原则如下:
需求分析-总体设计-模块分割 -建立数学模型-解数学模型的算法-程序编制-调试- 结果
在这个过程中,数据结构扮演着至关重要的角色。数据结构涉及到数学模型的建立和对该模型具体实现的对应的算法。它不仅是数学模型与计算机实现之间的桥梁,也是算法设计和程序编制的基础。通过选择合适的数据结构,我们能够优化算法的性能、提高程序的执行效率,从而更好地解决任务。
数据结构的地位在于数学、硬件和软件之间。它既是数学理论在计算机科学中的应用体现,又是计算机硬件和软件之间的桥梁。通过数据结构的学习和实践,我们能够更好地理解计算机科学的核心原理和技术,为未来的学习和工作打下坚实的基础。
因此,数据结构作为核心专业基础课,对于计算机专业的学生来说具有重要意义。通过这门课程的学习,我们可以掌握数据结构的基本概念、原理和方法,提高问题解决的能力和水平,为未来的职业发展奠定坚实的基础。
二、什么是数据结构
直观地说,数据是描述客观事物的数字、字母和符号,是计算机程序使用和加工的“原料”。数据的基本单位是数据元素,性质相同的数据元素的集合叫做数据对象。数据对象中的元素彼此之间的相互关系叫做结构。
数据结构举例:
图书馆的一本图书由书名、作者、出版社等数据来描述,根据需要我们选择其中的若干项组成一个数据元素来对应一本书。图书馆的编目表反映了书与书之间的关系,是数据元素之间的结构。当然我们还应注意到书是具体地放在某个书架上的,它是编目表的物理实现。图书馆从两方面管理图书:物理的藏书和逻辑的编目表。这就是图书馆的结构。和图书馆一样计算机管理数据,也有两个方面:即物理的存储和逻辑的关系。
例如问题模型涉及到的数据结构与算法:
结构分析—— 线性方程组
人口预报—— 微分方程
优化问题—— 线性规划、非线性规划
震动问题—— 矩阵分析;特征值、特征向量
信息管理—— 二维数据表
下棋 —— 树型结构
交通管理—— 图型结构
由此统一定义数据结构的基本概念和术语如下:
1.基本术语
(1)数据:描述客观事物的数字、字符以及所有能输入到计算机中并被计算机程序处理的符号的集合。(数字、字符:声音、图形、图像等等)
(2)数据元素:数据的基本单位,在计算机程序中常常作为一个整体进行考虑和处理,如纪录/结构。(3)数据项:数据的不可分割的最小单位,如结构中的域,(4)数据对象:性质相同的数据元素的集合,是数据的一个子集。
2.数据结构
(1)定义:是相互之间存在一种或多种特定关系的数据元素的集合。另一种定义:按照逻辑关系组织起来的一批数据,按一定的存储方法把它存储在计算机中,并在这些数据上定义了一个运算的集合。
三、数据的逻辑结构和存储结构
1.数据结构
数据结构是指互相之间存在着一种或多种关系的数据元素的集合。数据结构是一个二元组 Data_Structure =(D,R),其中,D是数据元素的有限集,R是D上关系的有限集。
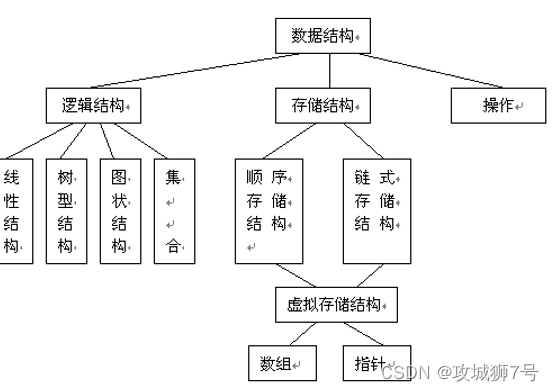
2.逻辑结构:是指数据之间的相互关系。通常分为四类结构:
(1)集合:结构中的数据元素除了同属于一种类型外,别无其它关系。
(2)线性结构:结构中的数据元素之间存在一对一的关系。
(3)树型结构:结构中的数据元素之间存在一对多的关系。
(4)图状结构:结构中的数据元素之间存在多对多的关系。
3.存储结构:是指数据结构在计算机中的表示,又称为数据的物理结构。通常由四种基本的存储方法实现:
(1)顺序存储方式。数据元素顺序存放,每个存储结点只含一个元素。存储位置反映数据元素间的逻辑关系。存储密度大。但有些操作(如插入、删除)效率较差。
(2)链式存储方式。每个存储结点除包含数据元素信息外还包含一组(至少一个)指针。指针反映数据元素间的逻辑关系。这种方式不要求存储空间连续,便于动态操作(如插人、删除等),但存储空间开销大(用于指针),另外不能折半找等。
(3)索引存储方式。除数据元素存储在一组地址连续的内存空间外,还需建立一个索引
表,索引表中索引指示存储结点的存储位置(下标)或存储区间端点(下标)。
(4)散列存储方式。通过散列函数和解决冲突的方法,将关键字散列在连续的有限的地址空间内,并将散列函数的值解释成关键字所在元素的存储地址。其特点是存取速度快,只能按 关键字随机存取,不能顺序存取,也不能折半存取。
顺序存储结构和非顺序存储结构的不同:
顺序存储结构是逻辑上相邻的数据元素存锗在物理位置上相毗邻的存储单元里,元素的关系由存储单元的邻接关系来体现。非顺序存储结构是数据元素可以在计算机内任意位置上存放(它不要求逻辑上相邻的元素在物理位置上也相邻),它们的逻辑关系用指针来链接。所以非顺序存储结构又叫链式存储结构。链式存储结构将数据元素存放的存储单元分为两个部分,分别存放数据和指针,称为数据域和指针域。
四、数据类型和数据结构
·数据值:atomic data value: 不可再分解。如3、2、5等。
nonatomic data value: 可以再分解,其成分称为data element 或 element。如
set: { 32.99, -1.03, 0,23} 。
·类型:同一类别可供识别的一组个体。
·数据类型:data value + operation 或者如下定义
1、A set of value
2、A set of operations on the these value。
·数据类型的类别:
1、原子数据类型:
数据值是原子数据值。如:int
2、结构数据类型:
数据值是可以再分解。如:如:sample array[1..3 ] of real

数据值的进一步分解为数据元素,它们之间有一个关系。
· 数据结构:
是一种数据类型,它的数据值为:
1、可以进一步分解为数据元素的集合,该数据元素可以是原子数据值,也可以是
另外一种数据结构。
2、数据元素之间有一个关系的集合。
注意:在许多数据结构的书籍之中,通常将数据元素称之为结点,但本书例外。
· 数据结构的分类:
1、线性结构:即:线性表:空或一个元素或:除第一个结点外,都有直接后继结点,
除最后一个结点外,都有直接前驱结点。
2、非线性结构:树、二叉树、图等。
· 实现:
1.ADT(Abstract Data Type): 认为 DT 仅存在于想象之中。注意力集中在感兴趣的性质 上,不关心数据的表示形式,操作的具体代码等等。给出规范或说明。
2.VDT(Virtual Data Type): DT 存在于 Virtual processor 上。如: c++ = O.S + hardware + c++ compiler 的 Virtual processor。其他如 SQL Virtual processor 等 。给出表示和实现。如:用类、类属数据类型、模板等。
3.PDT(Physical Data Type):DT 存在于物理机器上。
举例线性表ADT

举例线性表VDT

通常数据结构和算法的教科书,直接给出VDT。
五、算法
定义:指一系列确定的而且是在有限步骤内能完成的操作,
举例:

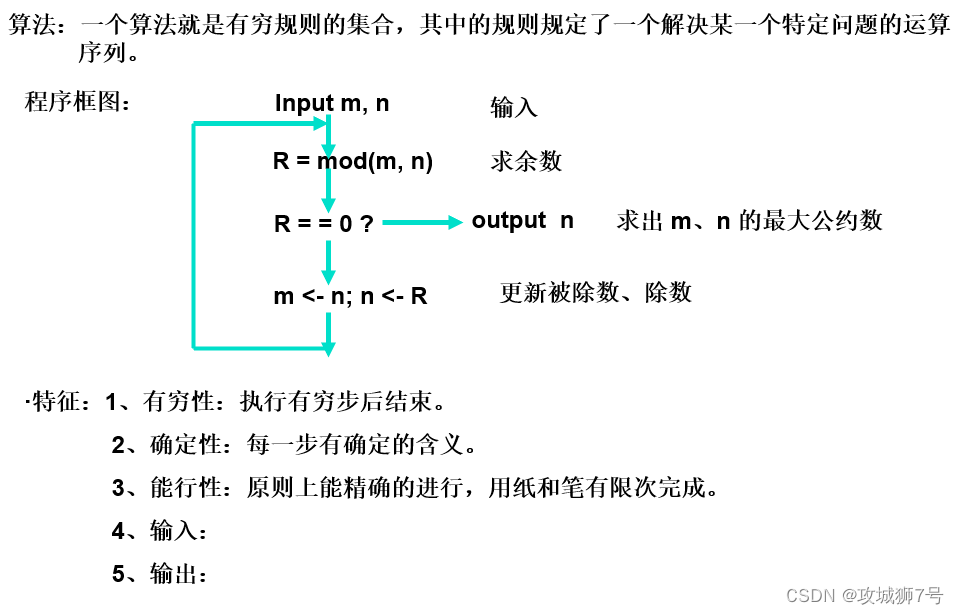
六、算法与数据结构的关系
数据计算机科学家沃斯(N.Wirth)提出的: “算法+数据结构=程序”。
揭示了程序设计的本质:对实际问题选择一种好的数据结构,加上设计一个好的算法,而好的算法很大程度上取决于描述实际问题的数据结构。算法与数据结构是互相依赖、互相联系的。
一个算法总是建立在一定数据结构上的;反之,算法不确定,就无法决定如何构造数据。
算法与数据结构关系举例
例1:
编写程序查询某城市某人的电话号码建立一张登记表
存放2个数据项:
姓名+Te1
好的算法取决于这张表的结构及存储方式:
将表中结点按照姓名顺序地存储在计算机中,依次查找可能遍历整个表都找不到。
建立一张姓氏索引表:姓+表中的起始地址则不需查找其他姓氏,查找效率得到提高。
例2:
设计一个考试日程安排表,使在尽可能短的时间安排完考试,要求同一个学生选修的几门课程不能安排在同一个时间内。
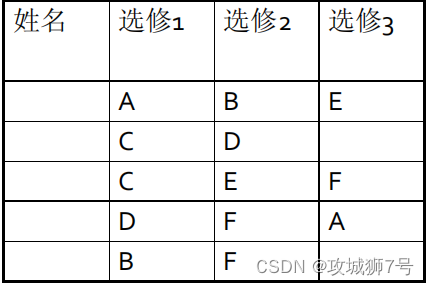
数据解决该问题,首先选择一个合适的数据结构。用无向图表示,图中的顶点表示课程,不能同时考试的课程之间连上一条边。则该问题就抽象成对该无向图进行“着色”操作,即用尽可能少的颜色去给图中每个顶点着色,使得任意两个相邻的顶点着不同的颜色。同一种颜色表示一个考试 时间。
解决问题的关键步骤是先选取合适的数据结构表示问题才能写出有效的算法。
算法设计的要求
(1)正确性
(2)可读性
首先是给人读,然后才是机器执行
(3)健壮性 容错性
4)效率与低存储量需求
七、算法时间复杂度和空间复杂度
算法的时间复杂度:
以基本运算的原操作重复执行的次数作为算法的时间度量。一般情况下,算法中基本运算次数T(n)是问题规模n(输人量的多少,称之为问题规模)的某个函数f(n),记作:T(n)=O(f(n))也可表示 T(n)=m(f(n)),其中 m为常量。记号“O”读作“大 O”,它表示随问题规模n的增大,算法执行时间 T(n)的增长率和f(n)的增长率相同。
注意:有的情况下,算法中基本操作重复执行的次数还随问题的输人数据集不同而不同。常见的渐进时间复杂度有:0(1)<0(log₂n)<О(n)<О(nlog₂n)<О(n^2)<О(n^3)<O(2^n)<0(n!)<O(n^n)。
算法的空间复杂度:
是对一个算法在运行过程中临时占用的存储空间大小的量度。只需要分析除输入和程序之外的辅助变量所占额外空间。
原地工作:若所需额外空间相对于输入数据量来说是常数,则称此算法为原地工作,空间复杂度为0(1)。
程序运行时间影响因素:
1、 输入规模
2、利用编译程序生成的目标代码的质量
3、计算机程序指令系统的品质和速度
4、算法的时间复杂性的函数
1、4 点自明。2、3两点表示算法的时间依赖于软件和硬件的环境。或者说用在某一系统 中的绝对时间,判断算法的优劣是不正确的。或者,换句话说,时间复杂性函数不能采用 在某一机器上运行的绝对的时间单位,如秒、分… 作为衡量算法的优劣。
时间复杂度的度量:





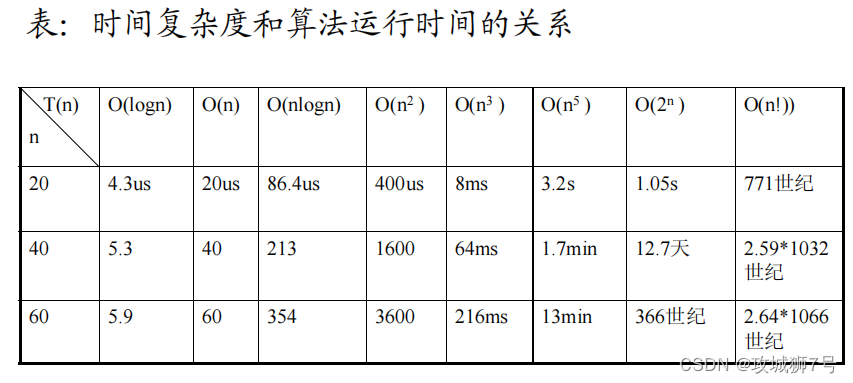




100:[NOIP2008]ISBN号码101:kotori和迷宫102:矩阵最长递增路径](https://img-blog.csdnimg.cn/direct/a70135781b8a46db952efaa48cd9e282.png)