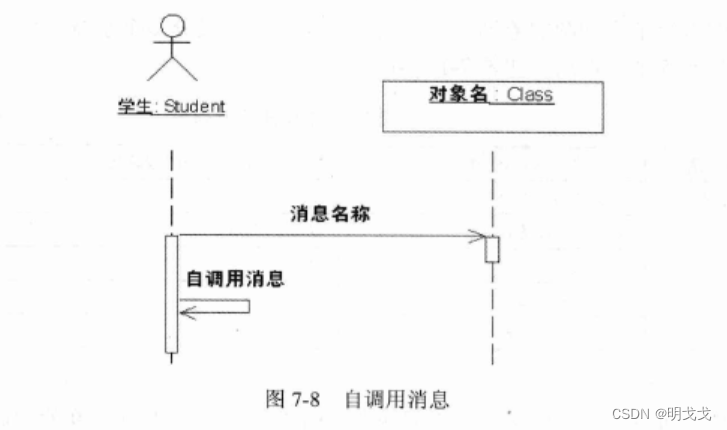
Antialiasing
实际的图形学中是怎么实现反走样的呢?
我们不希望实际产出的图形有锯齿效果,那怎么办呢?
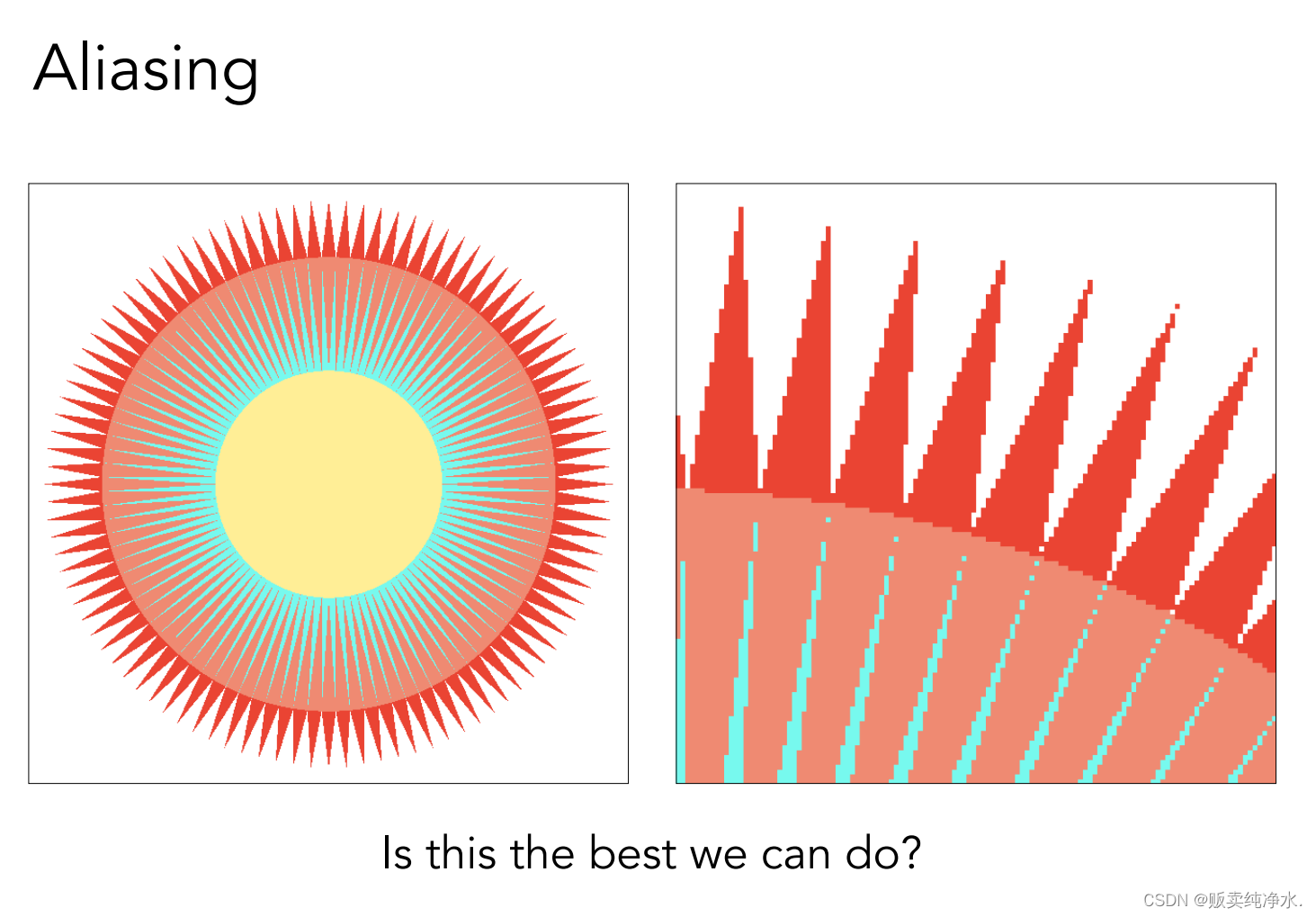
从采样的理论开始谈起吧
Simpling theory
照片也是一种采样,把景象打散成像素放到屏幕上的过程:

还可以在不同的时间(视频):

动画是定义在帧数上的
一个专业术语:Artifacts(瑕疵)
采样会产生很多问题,一个是锯齿:
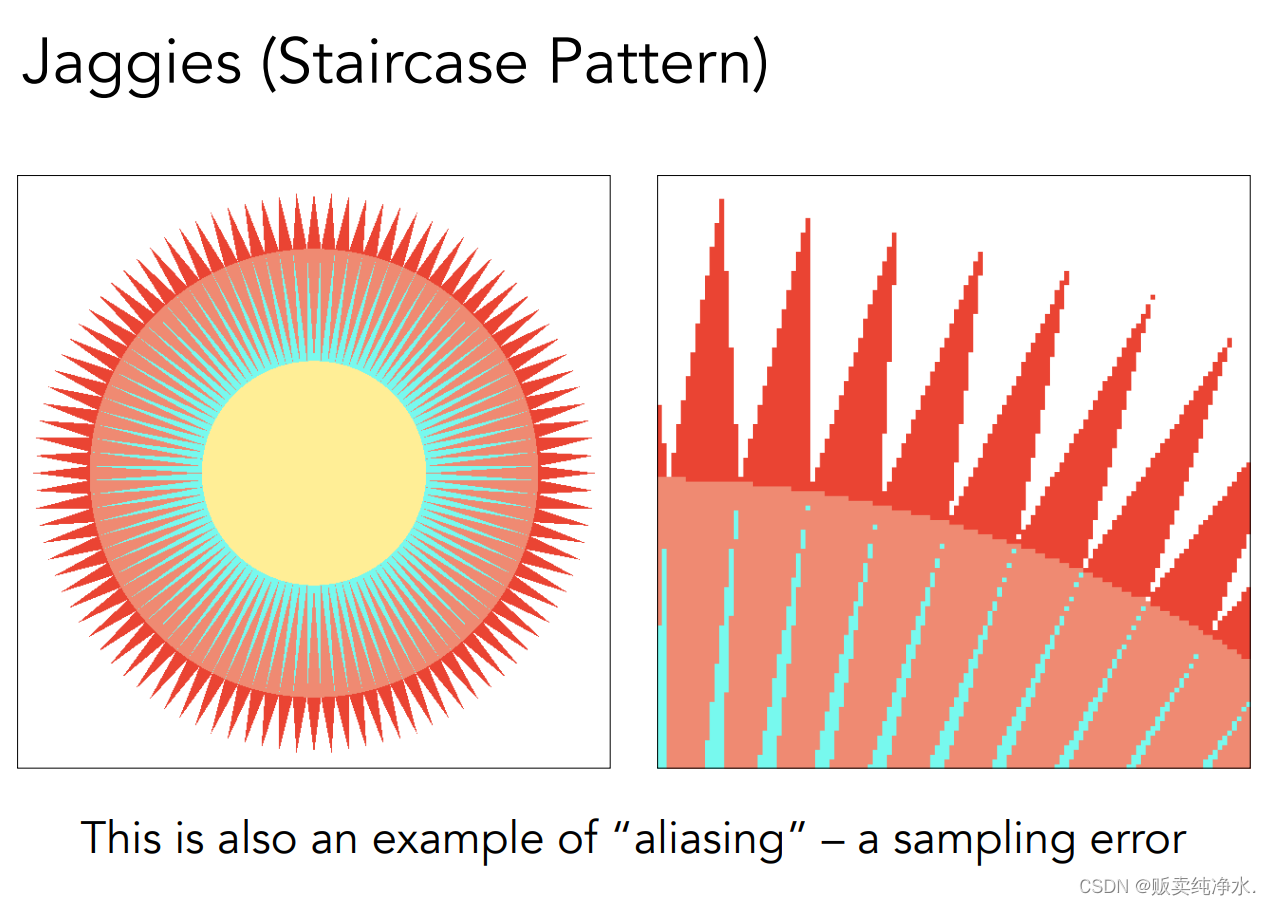
还有问题比如说摩尔纹:

它怎么产生的呢?
比如说把左边的奇数行奇数列都去掉变成小图,显示成和大图一样大,就能看到摩尔纹了(拿手机拍电脑显示器)
还有一种有意思的叫车轮效应,也是采样中出现的问题,比如人肉眼的采样速度跟不上高速旋转的物体:

我们如何反走样呢?
在采样之前做一个模糊(滤波),做一个模糊再采样就可以反走样:
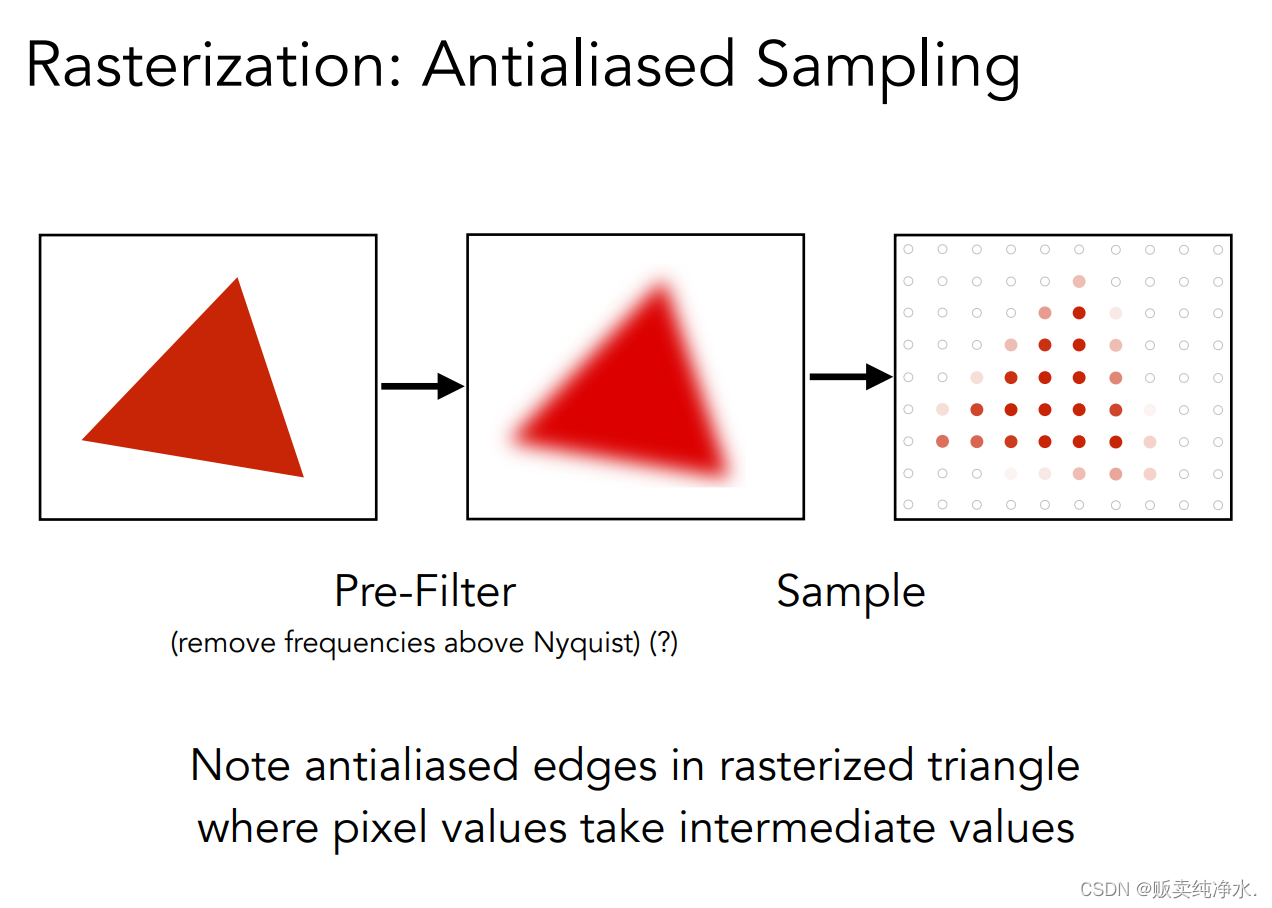

注意顺序是不能颠倒的,要先模糊再采样,如果先采样再模糊就变成了Blurred Aliasing:
 那为什么采样的速度跟不上信号变换的速度就会走样?
那为什么采样的速度跟不上信号变换的速度就会走样?
Antialiasing in practice
Frequency Domain
先来看看频率吧:
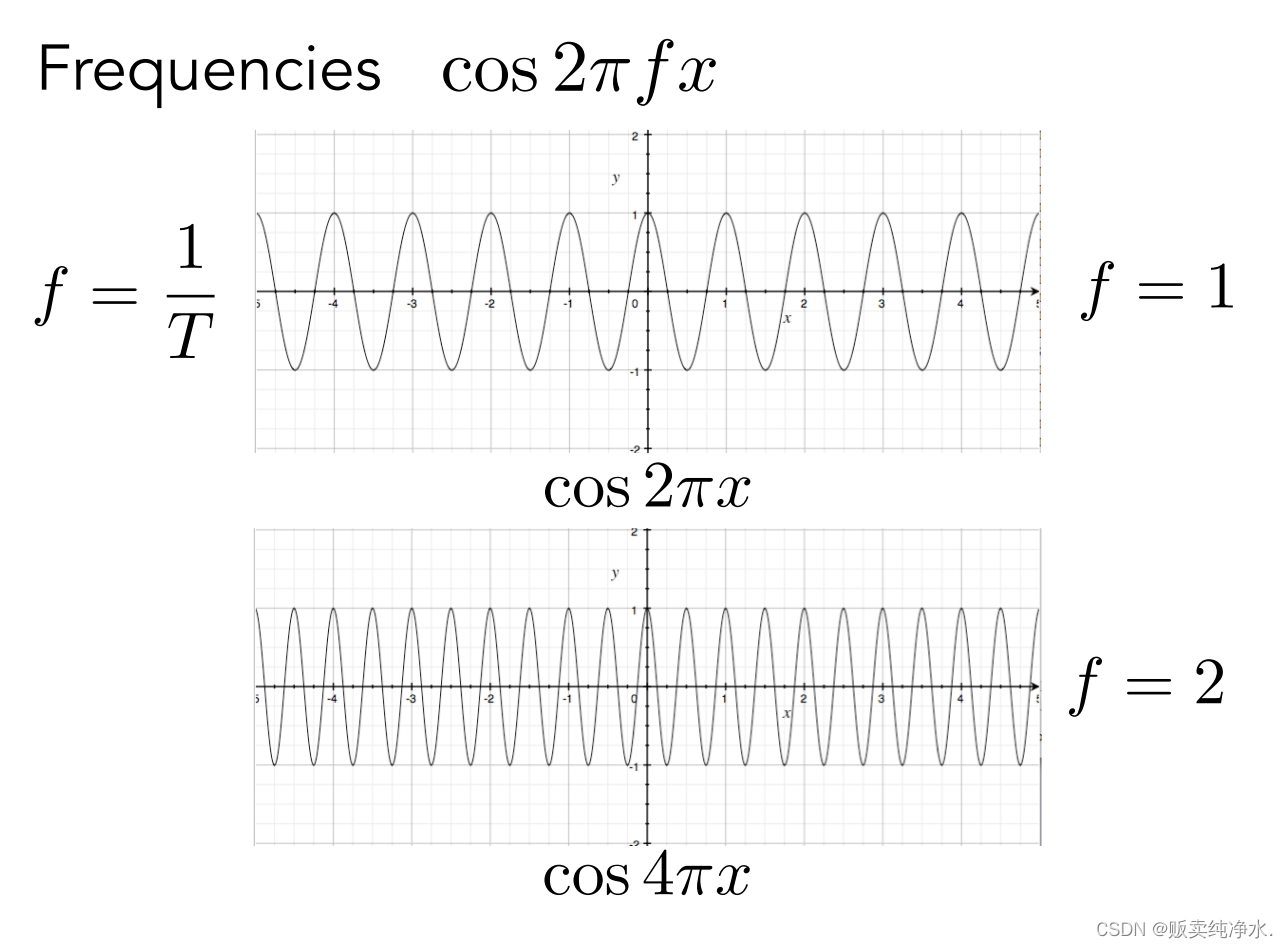
调整前面的系数会得到不同的余弦波(频率不同)
介绍正余弦波:
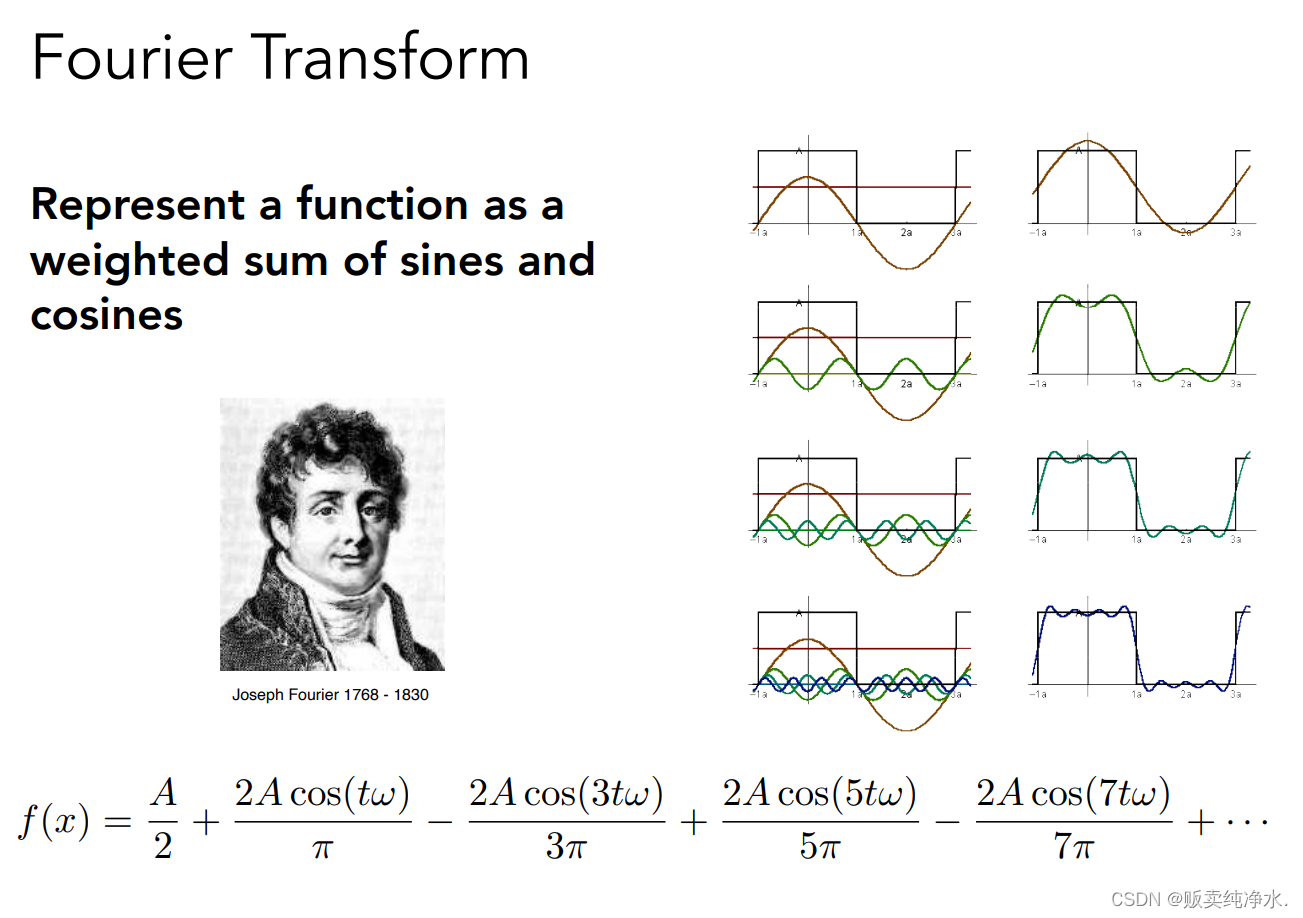
为了介绍傅里叶级数展开(任何周期函数可以将其写成正余弦函数的线性组合)
还有个东西叫傅里叶变换:
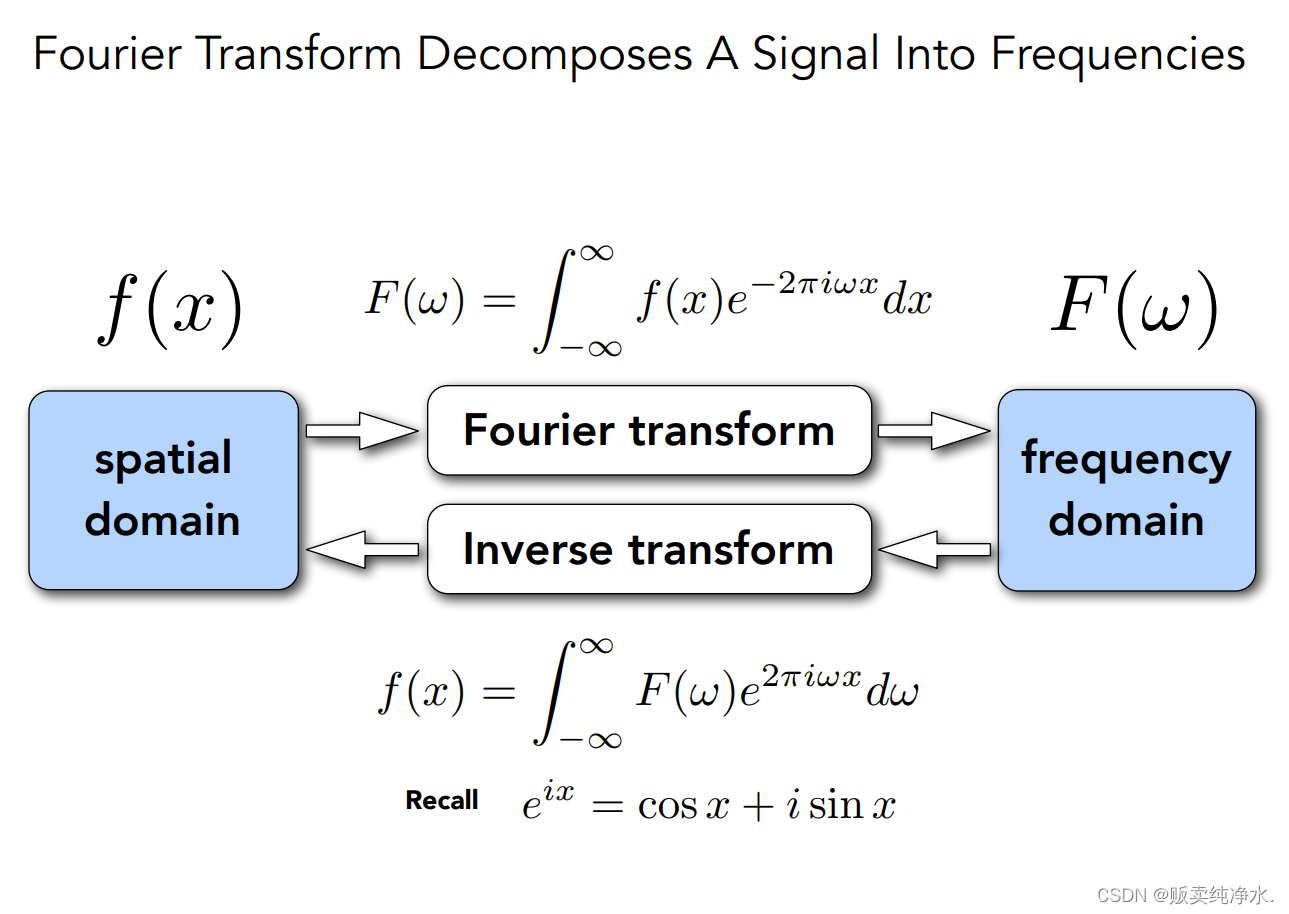
傅里叶变换:把函数变成不同频率的段并且显示出来:
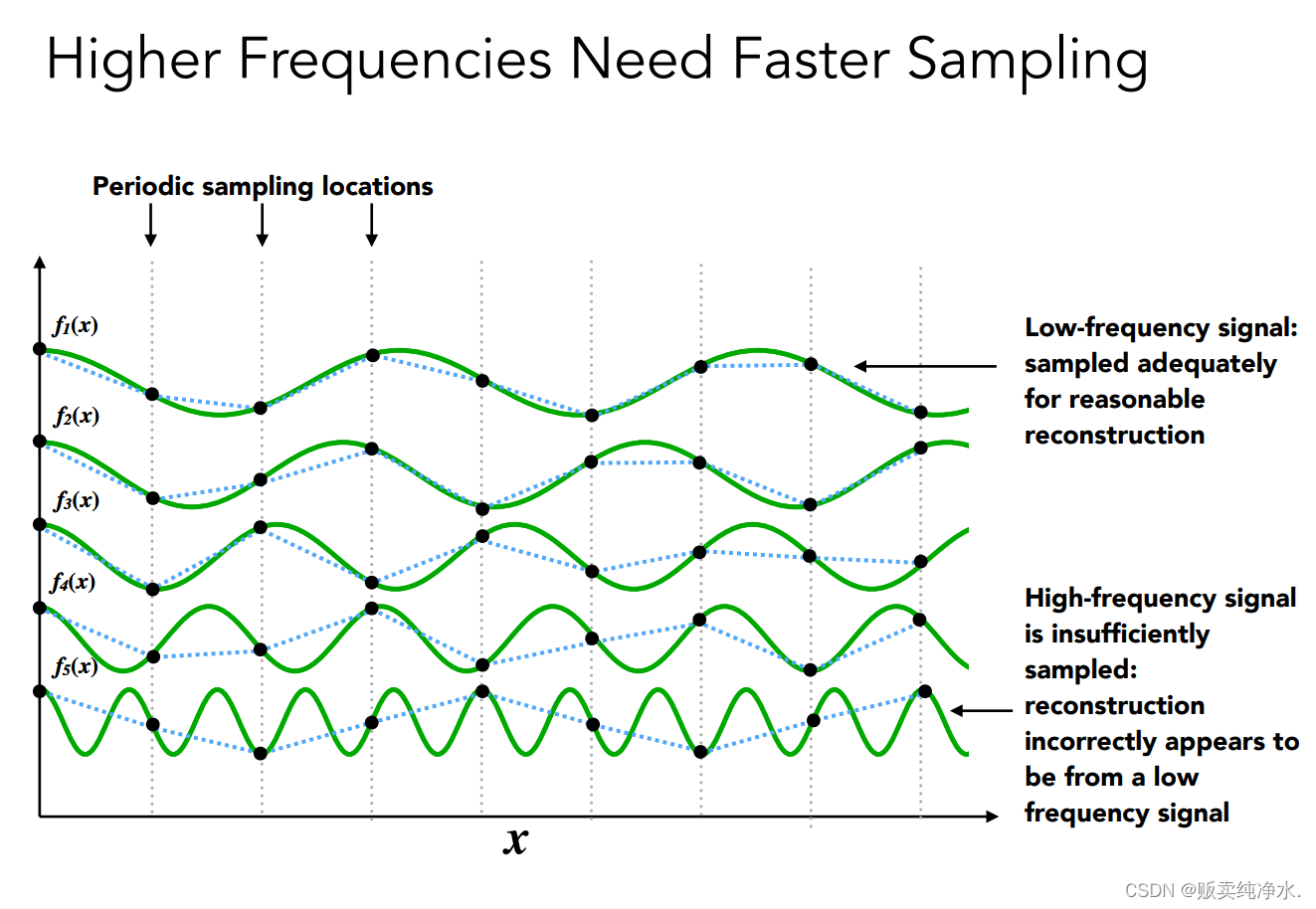 采样还原出的函数在不同频率下有出入,走样本质是信号变化的太快导致采样跟不上
采样还原出的函数在不同频率下有出入,走样本质是信号变化的太快导致采样跟不上
时域相乘,频域卷积,必须要到达两倍才不会走样
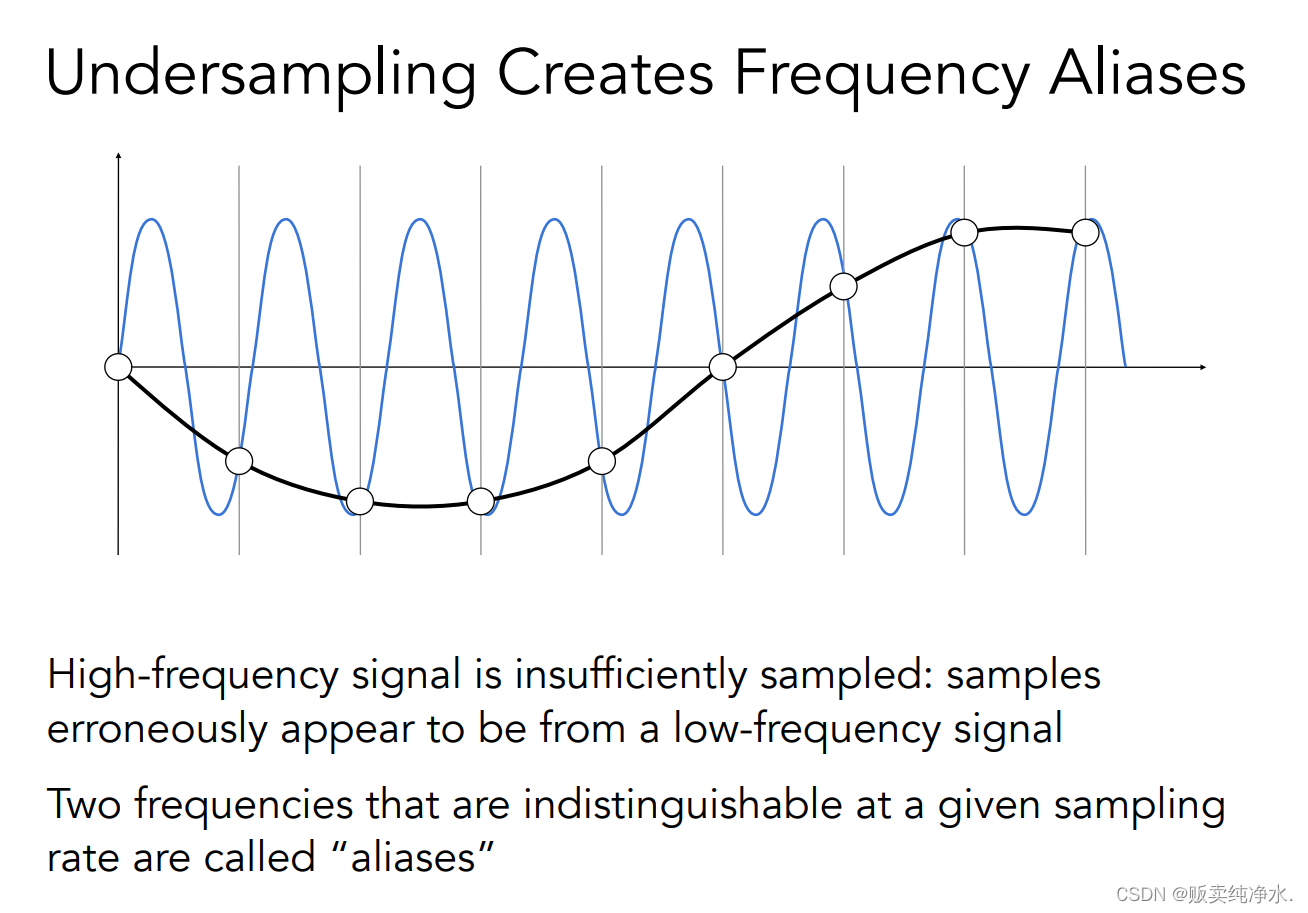
上面的结果就是采样两种频率完全不同的信号但是采样结果完全一样!
这就是走样。
Filtering
把某个特定的频率给抹掉,说出对应信号如何变化
傅里叶变换就是从时域变到频域:

中心把其定义成低频的区域,周围全都是高频的区域,在不同频率的信息多少通过亮度表示
信息多集中在低频段
水平和竖直方向有道,我们在分析信号的时候我们会认为它是周期性重复的信号,那么对于不周期性重复的信号怎么办呢?
比如上图哪里重复了,并不重复对吧,我们通过右边界在重复左边界的内容,在边界会产生剧烈的变化从而产生极其高的高频,头顶位置和衣服下边缘位置的图像变化剧烈,导致高频区域为白色
滤波是去掉一些频率的内容,把低频信号抹掉,高频信号有意义:图像内容的边界

这种滤波叫高通滤波 (通过滤波器使只有高频的滤波可通过)
为什么高频信息就对应边界呢?
是不是变化很剧烈的才叫边界?
那就是高频信息呀,我们如果过滤掉高频只留下低频呢?

会发现边界模糊勒
还可以做另外的实验:去掉高频。去掉低频,留下中庸之道,就可以提取到一些不是很明显的边界特征(中通滤波):

卷积(Convolution)和滤波有关系,本质是一种点乘:
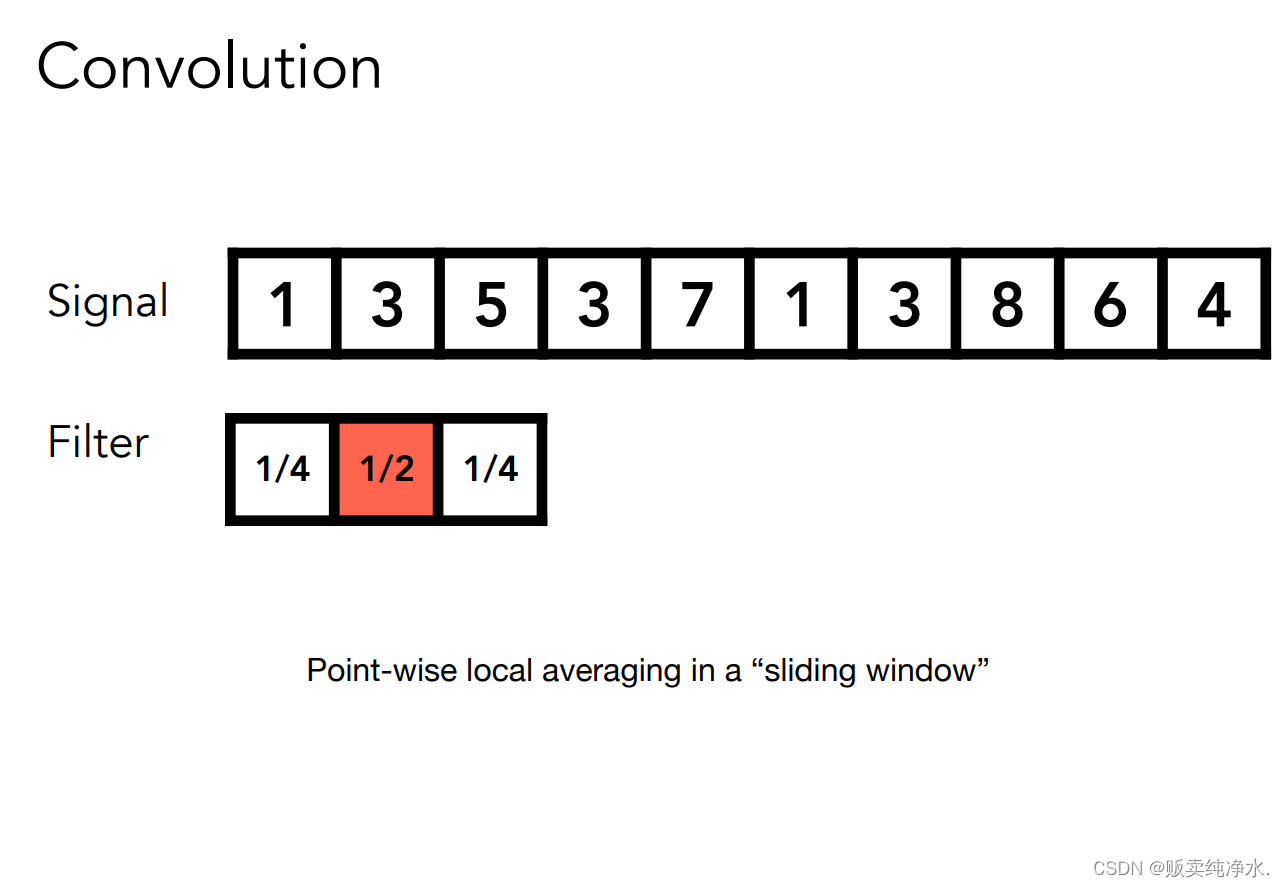
这是要做一个卷积操作(加权平均):
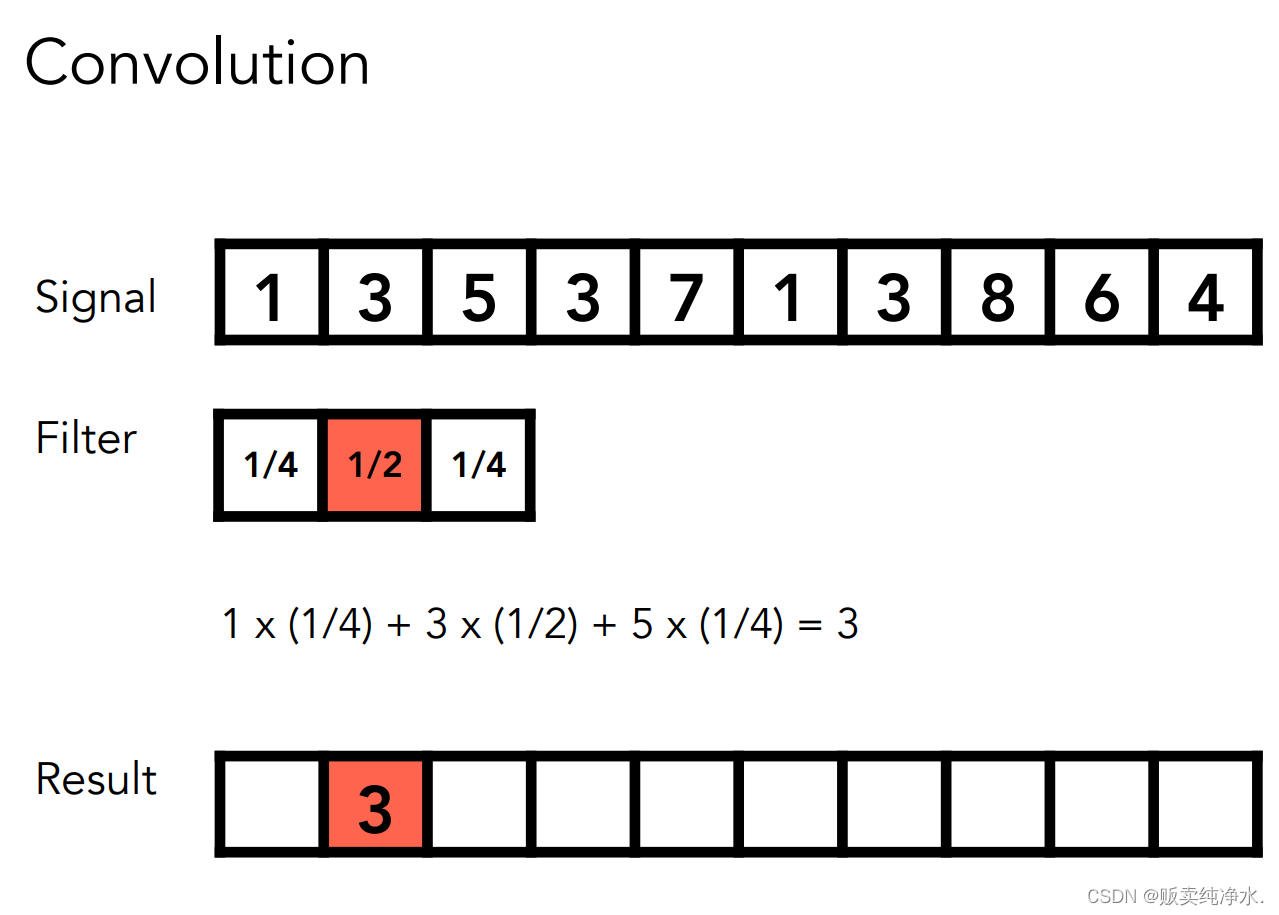
卷积定理: 时域卷积等于频域相乘,在时域上的乘积相当于在频域上的卷积:

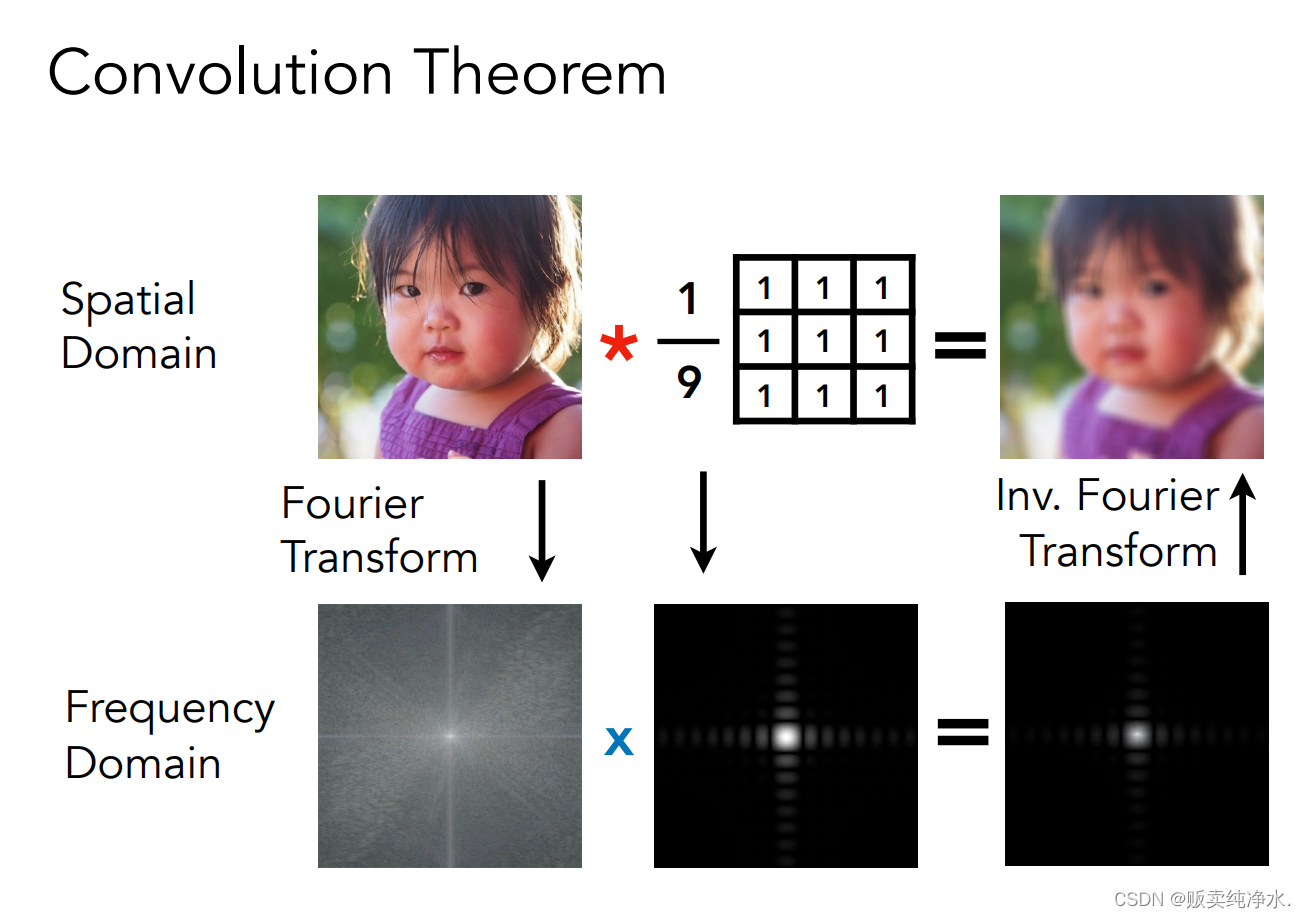
卷积操作进行均值模糊,时域的卷积等于频域的乘积
滤波器本身是一个3×3的盒子,再×是为了不让图像整体的颜色值发生变化:
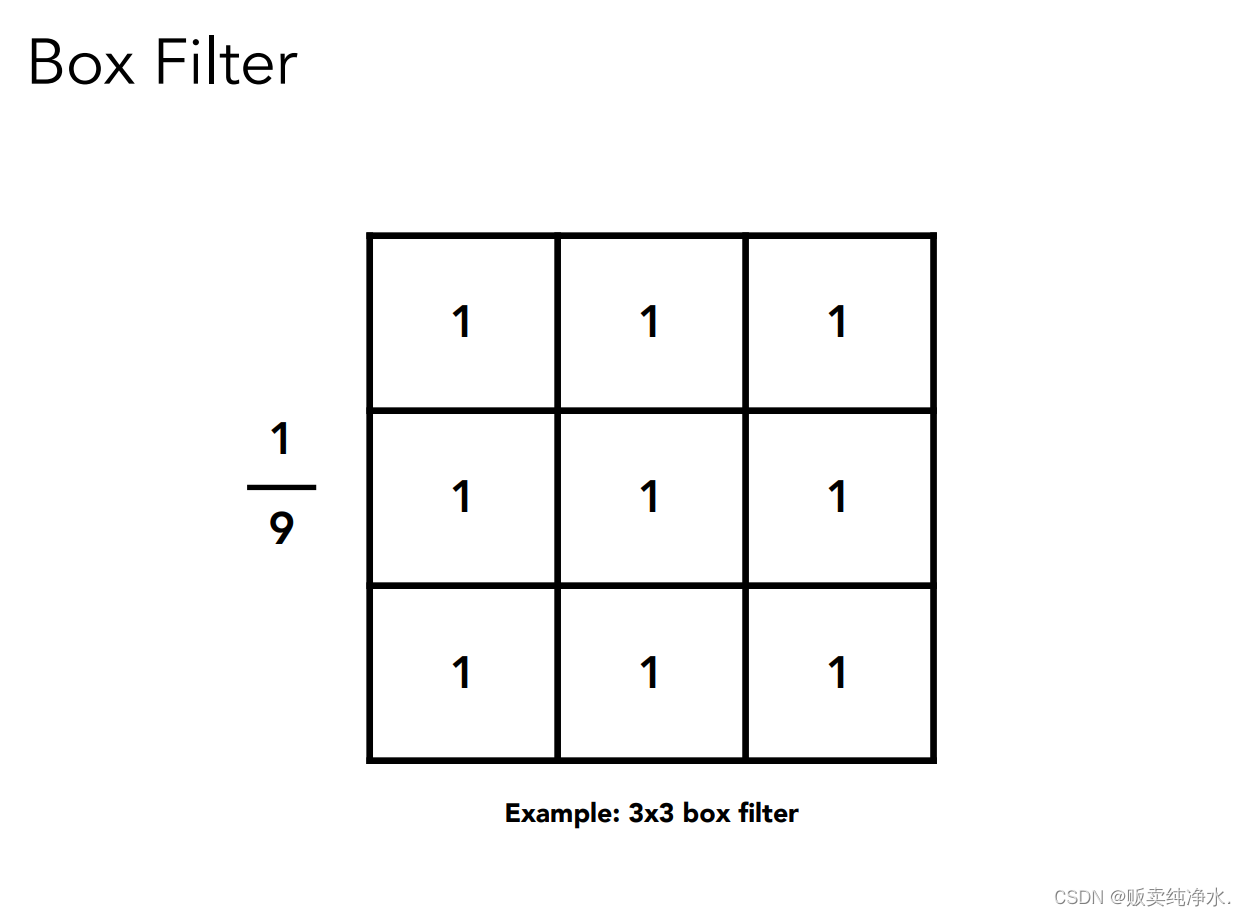
上面的例子显示出的结果是这个盒子是一个低通滤波器

时域上的一个小格子转换成频域,如果盒子在时域上变大了,那在频域上该如何变化呢?
盒子在时域上变大,反而在频域上变小:
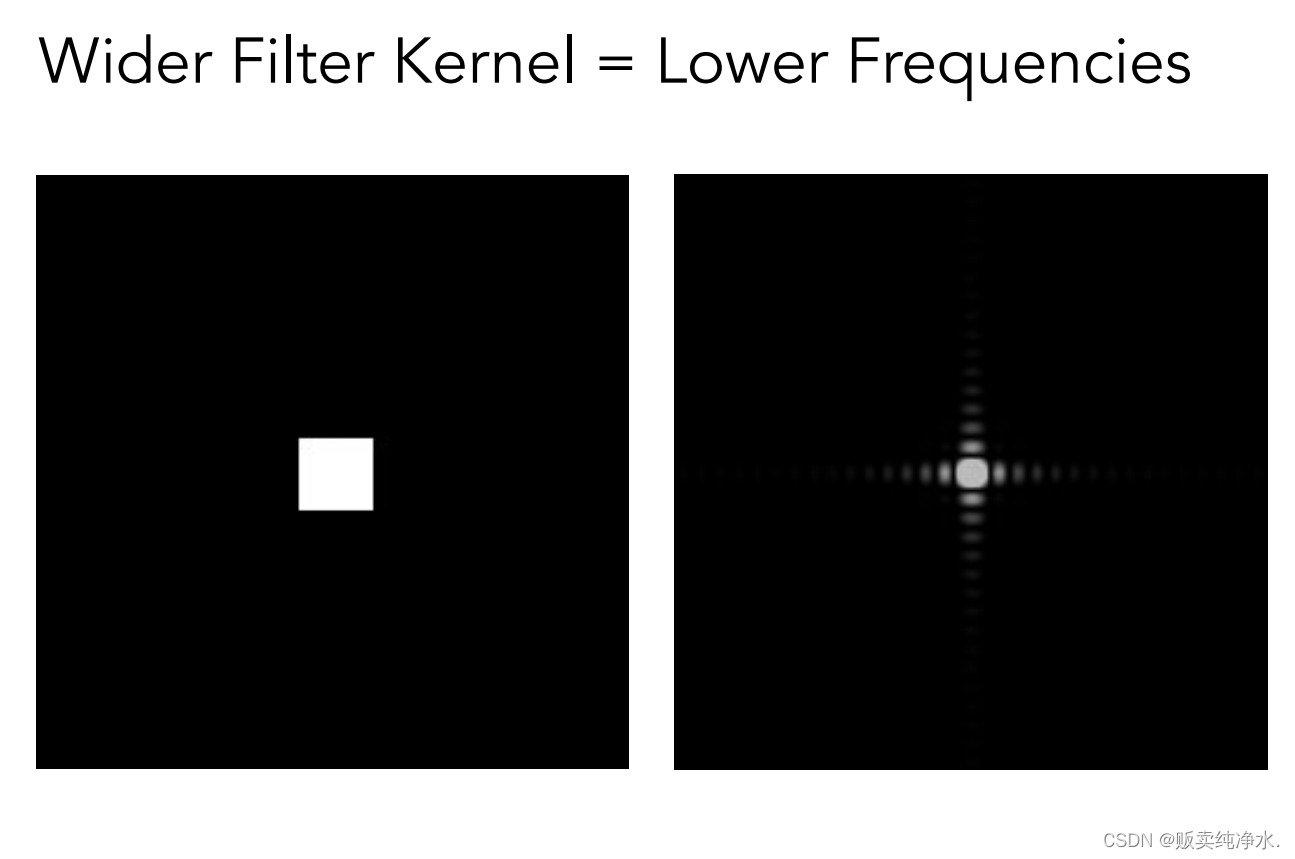
用越大的box做卷积会越来越模糊,如果用一个超级小的box就相当于根本没有做滤波,也就是说所有东西都被留了下来
采样是什么?是在重复频域上的内容(×另外一个函数):
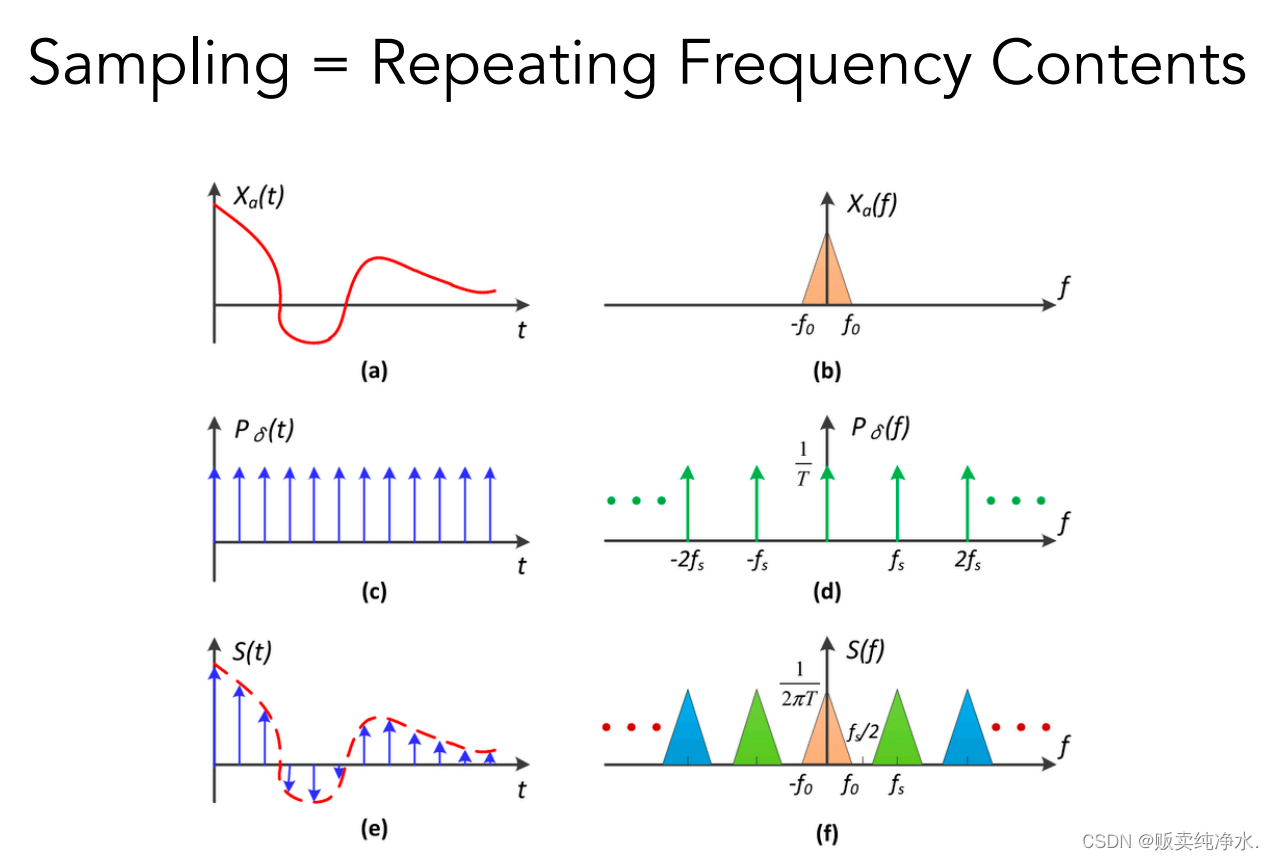
根据卷积定理,时域上的乘积对应到频域上为卷积,时域卷积等于频域乘积
采样就是在重复原始信号的频谱
1、左侧一列的中间是一个周期冲激序列,它在t=nT上纵坐标为无穷大,且频域(右中)仍是一个冲激序列,若用其与原信号相乘进行采样,采样的过程就不是让左边上中两图简单相乘就行了,它需要再进行一个过程将其转化为离散时间序列
2、实际采样时一个常用的办法是用一个在t=nT上纵坐标为1的采样序列乘信号源,这样可以直接得到采样信号
3、右上和右中卷积得到右下是可证的
为什么会产生走样就很显然了:采样的不同间隔会引起频谱以另外一个不同的间隔移动:
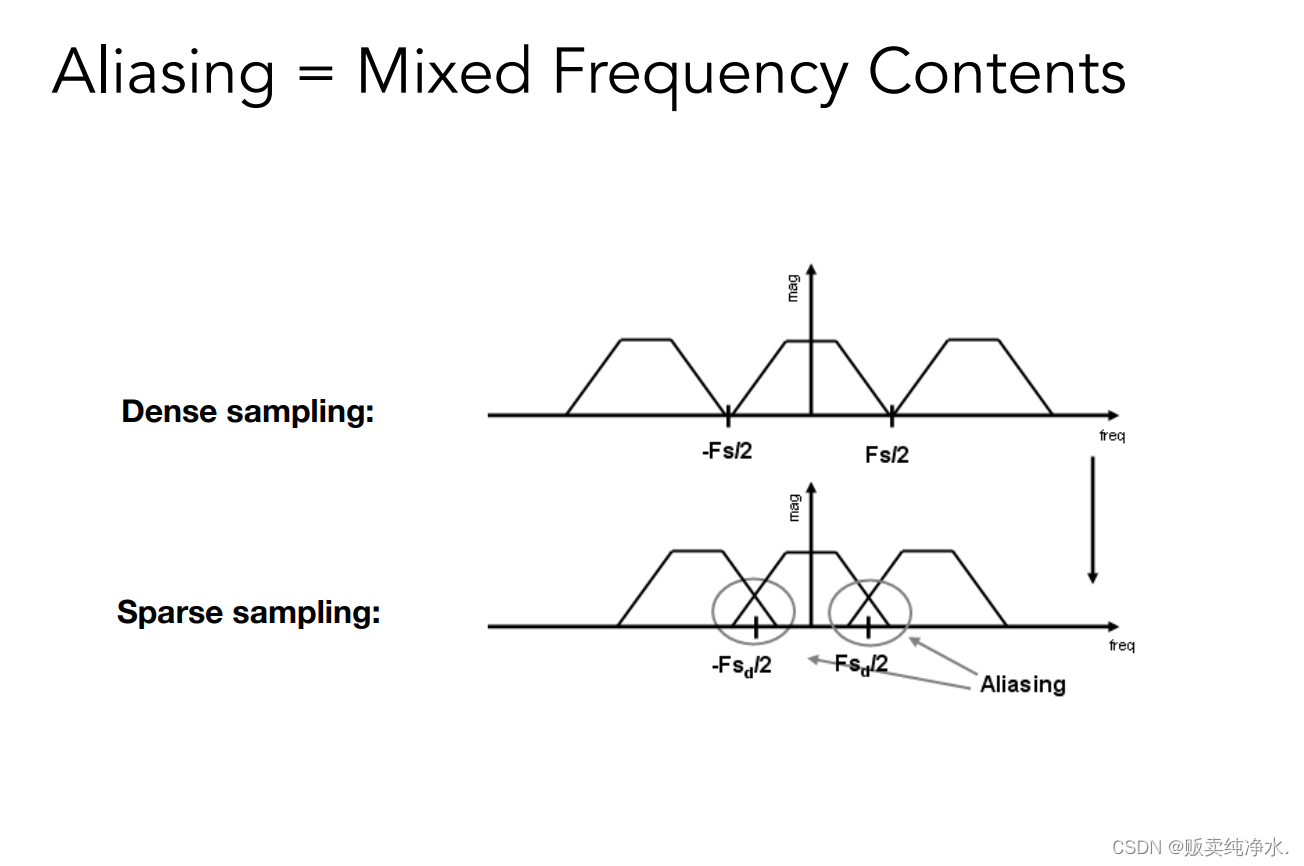
采样不够快,冲击函数频率低,卷积结果频率低(原始信号和复制粘贴的信号重合在一起了:发生走样,频谱搬移发生混合)
提升分辨率走样就会好很多(进行多的采样)
Reduce Alising
怎么改善走样呢?

1.提高分辨率
2.先去模糊再去采样(模糊:低通滤波):
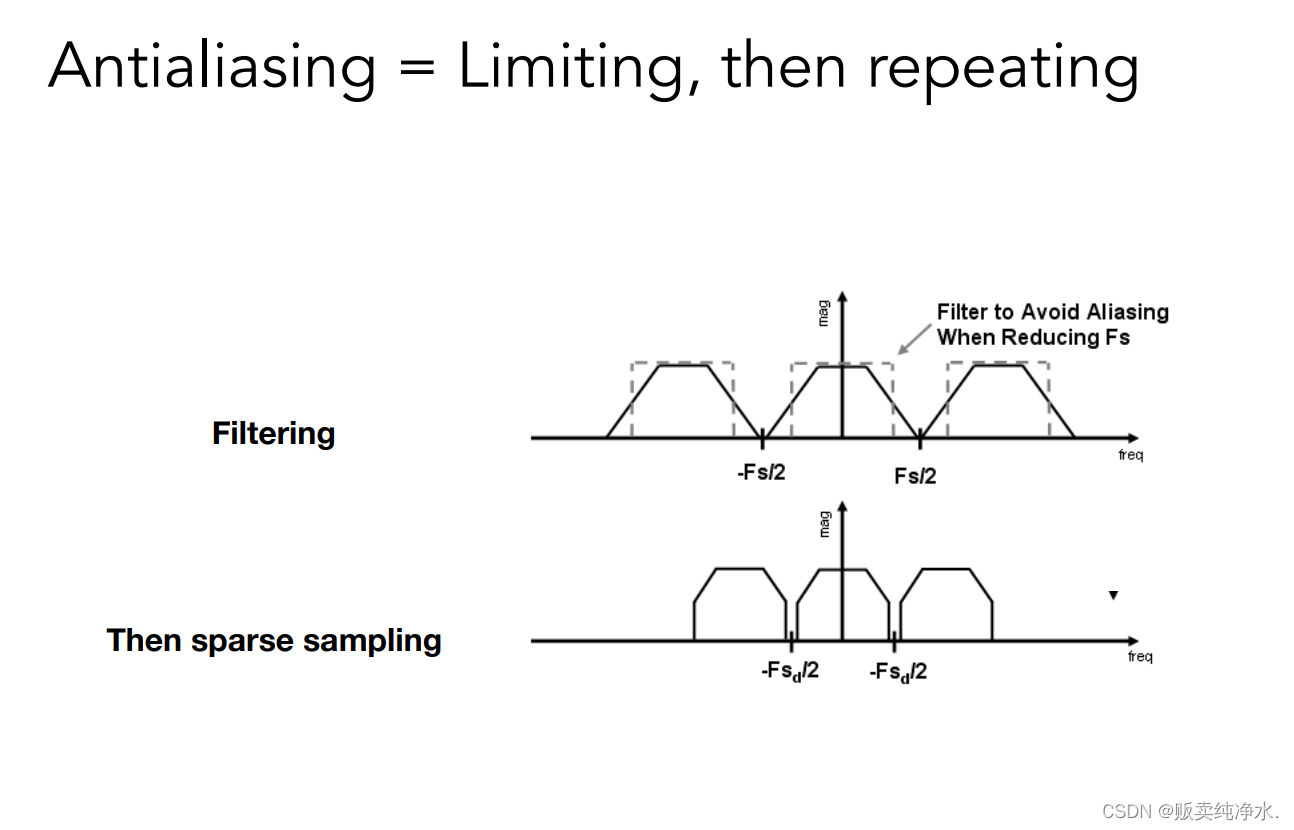
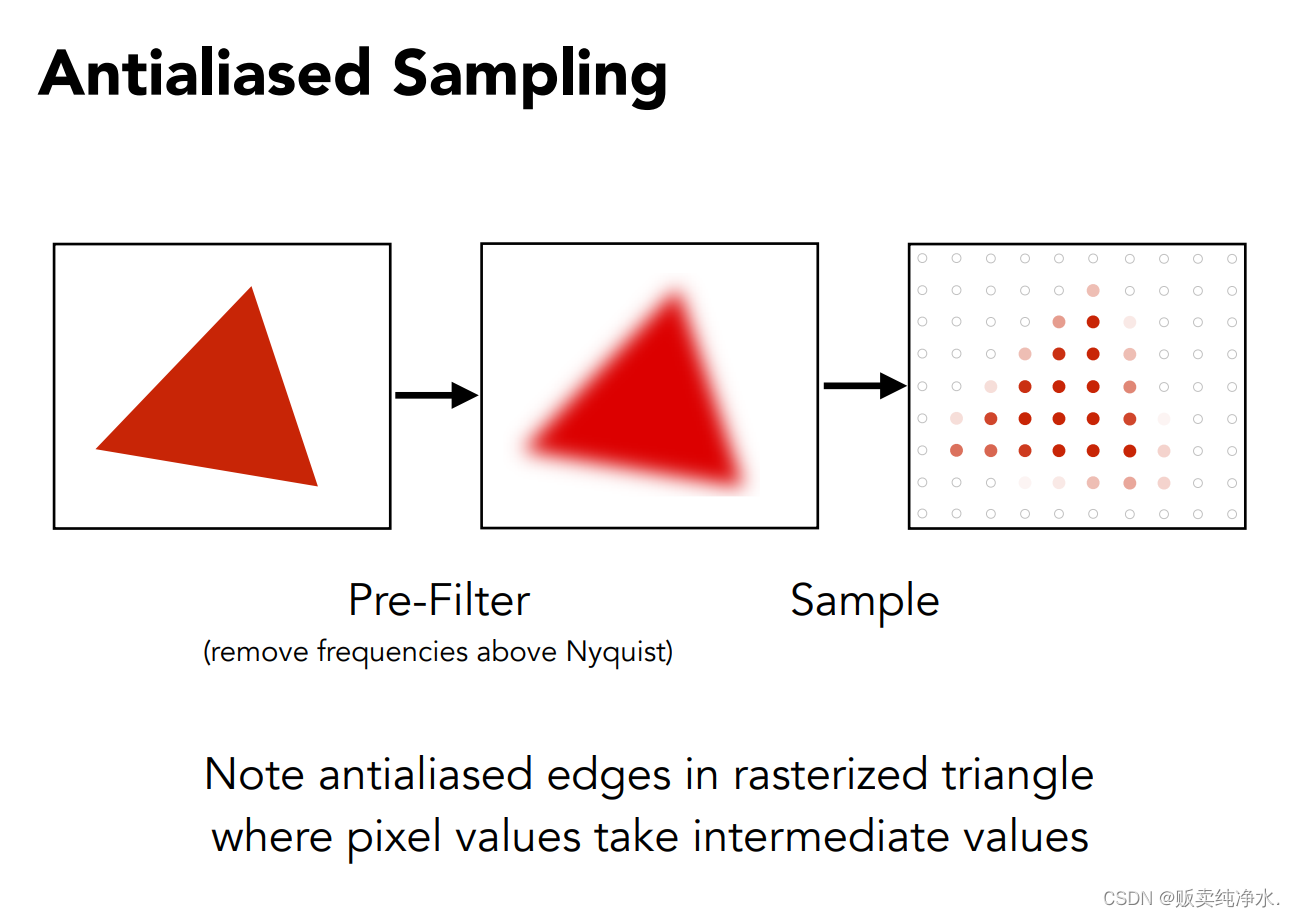 那么在实际的操作中,我们采用什么样的滤波器来进行卷积操作呢?
那么在实际的操作中,我们采用什么样的滤波器来进行卷积操作呢?
用一定大小的低通滤波器对其进行卷积:

对像素覆盖的面积求平均:
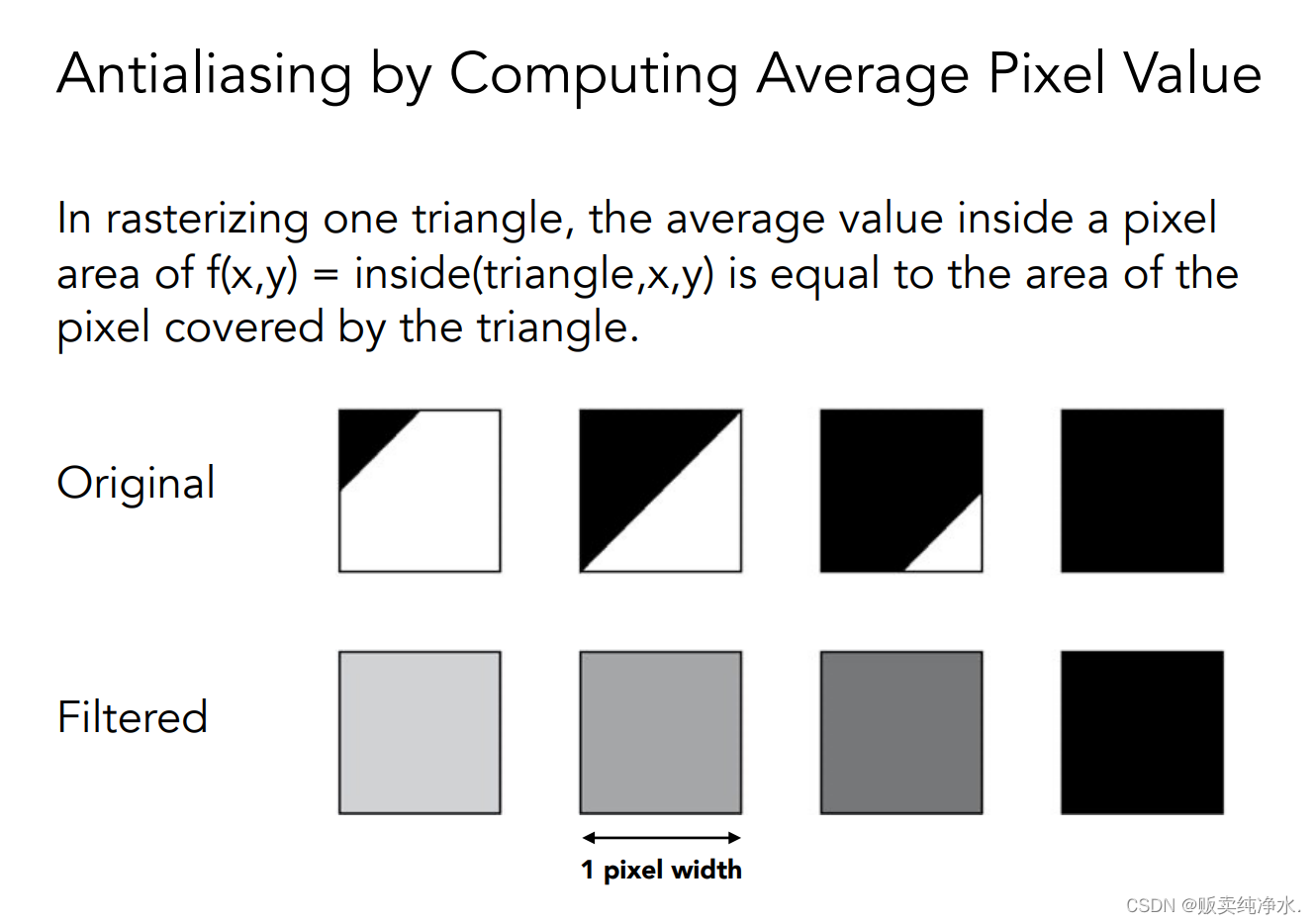
MSAA
对更多采样点进行反走样(对反走样的近似,不能严格意义上解决反走样的问题),对大覆盖的点的近似:
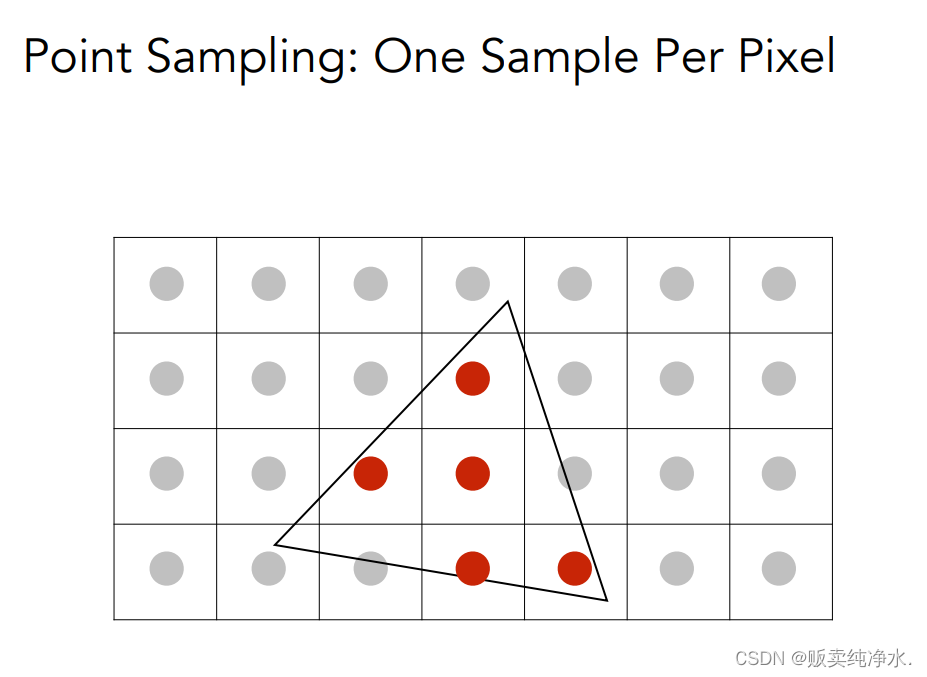

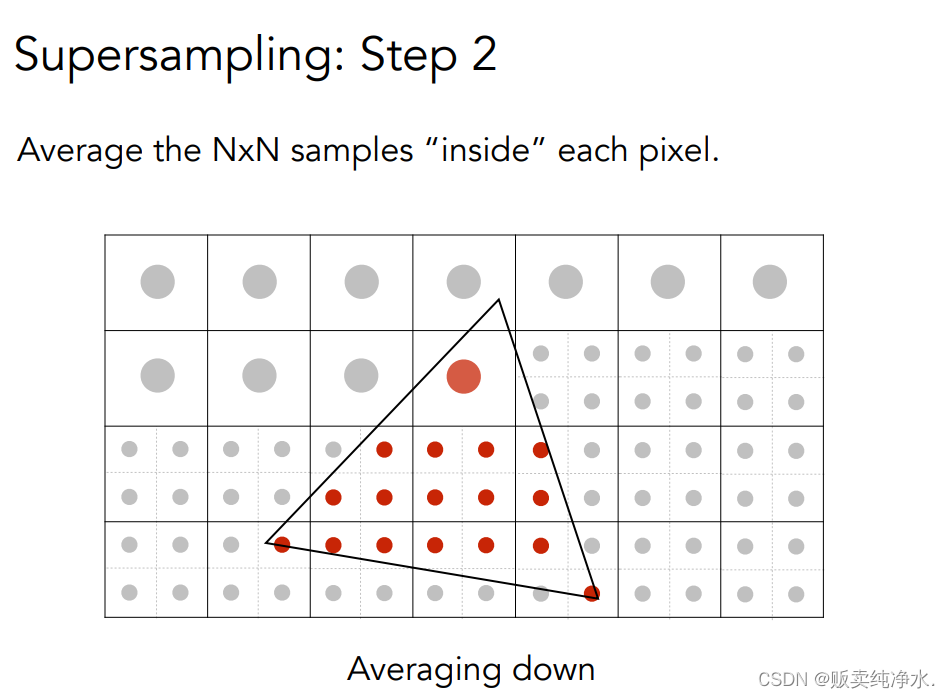
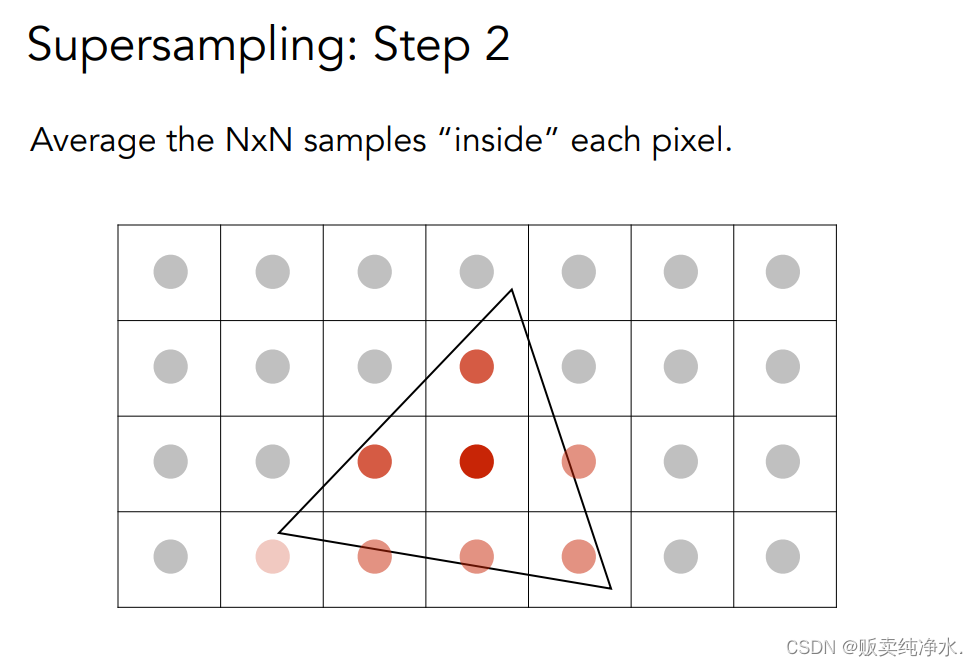
通过更多的样本进行反走样的第一步:模糊
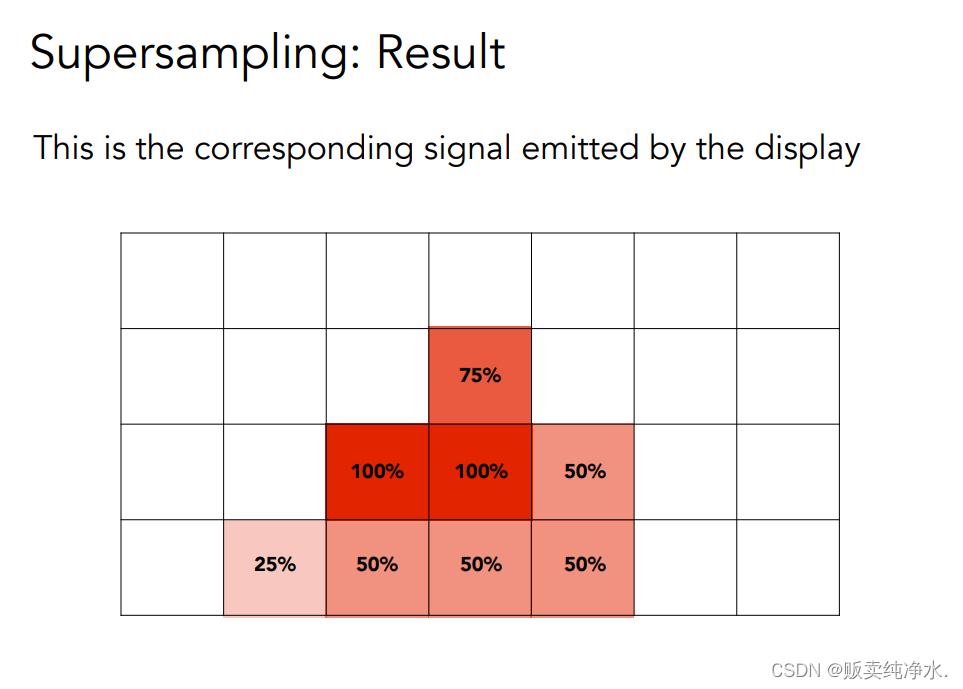
MSAA是采样时提升了计算精度:
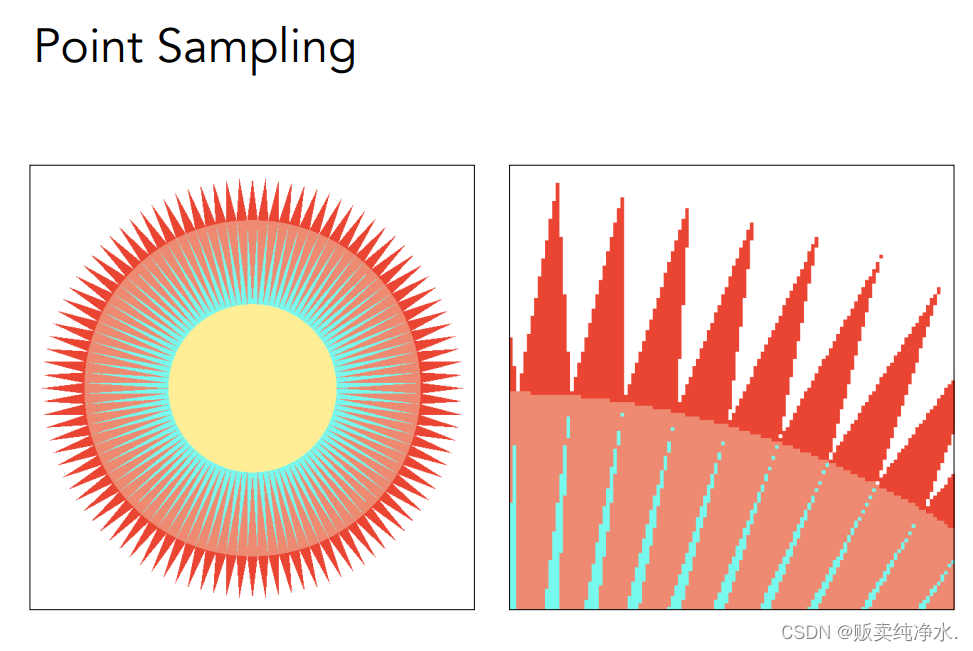
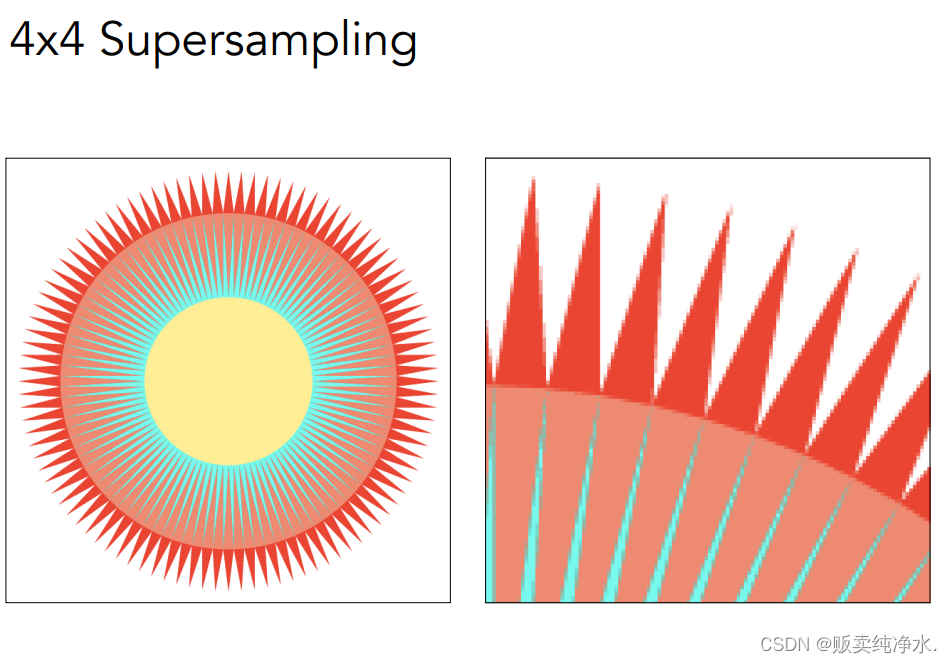
通过增大计算量抗锯齿,还有其他抗锯齿的方法:FXAA(Fast Approximate AA:替换成没有锯齿的边界)、TAA(Temporal AA:找上一帧的信息)
Tips:Super resolution,超分辨率,把小图放大看到的全是锯齿,怎样把采样不够的图变得没有锯齿呢?可以通过深度学习的方法:DLSS(猜测)
Visibility/occlusion
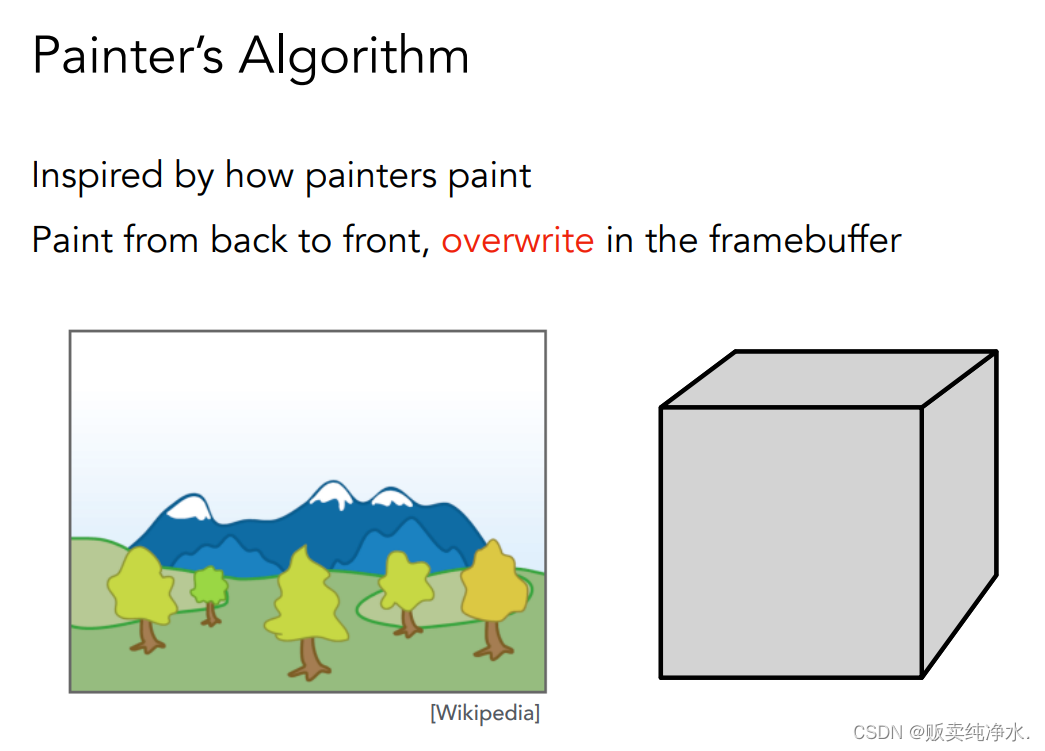
首先需要谈的问题就是关于可见性,很直观的一种想法是先画远处的物体,再画近处的物体(把远处的物体遮挡住),由远到近做光栅化:(Painter's Algorithm)画家算法:
但是想要定义深度并不简单,需要光栅化排序:
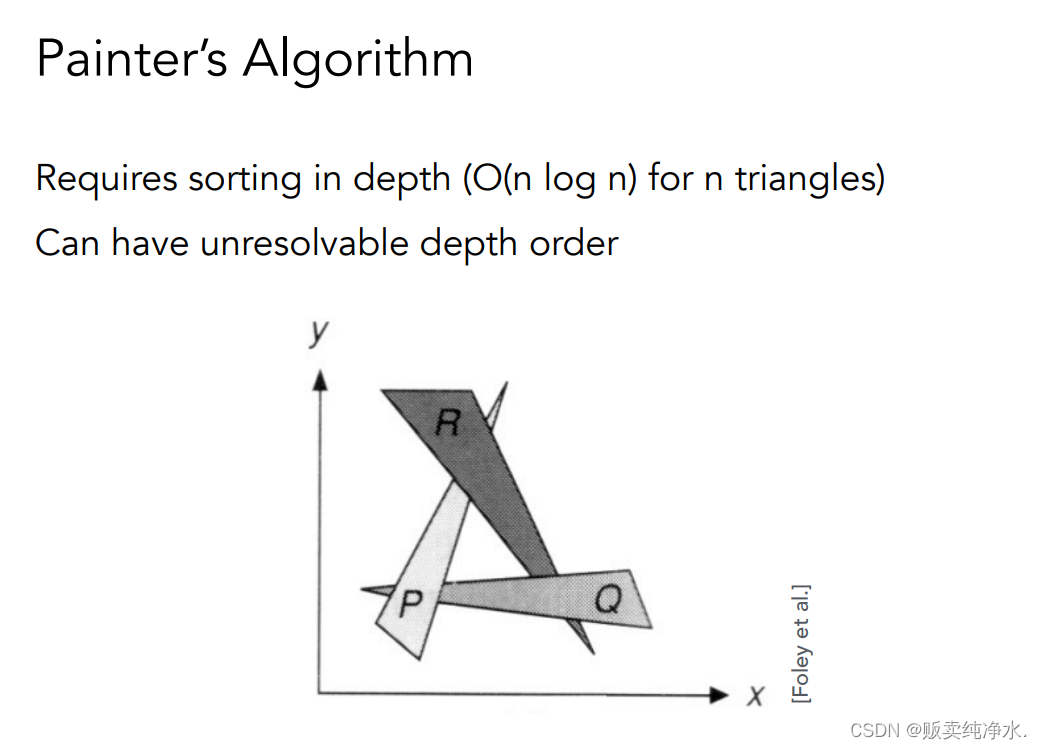
上面这种复杂的情况在深度上存在互相遮挡的关系,也就没办法用亲爱的画家算法,为了解决这个问题,在图形学中引入了一个概念:Z-Buffering
Z-Buffering
深度缓冲
对三角形的覆盖关系不好判断,但是可以面向像素排序,记录像素离我们比较近的距离
最后得到的结果是要渲染出一幅画面:

这两幅图永远都是同时生成的,那算法在一开始的时候该如何进行呢?
看像素的具体情况,更新最浅深度:

深度缓存工作实例:

涂新颜色、更新最小深度值
深度缓存算法有一个好处:与顺序无关,不会有两个浮点数的值完全一样(出现深度完全一样的情况),深度缓存算法被广泛的应用于图形学