如有不懂的地方，可查阅往期相关文章！

                    个人主页：小八哥向前冲~

                    所属专栏：数据结构【c语言】

---

目录

单值二叉树

对称二叉树

计算二叉树的深度

二叉树的前序遍历

相同二叉树

另一棵树的子树

二叉树的构建和遍历

翻转二叉树

判断平衡二叉树

---

单值二叉树

题目：

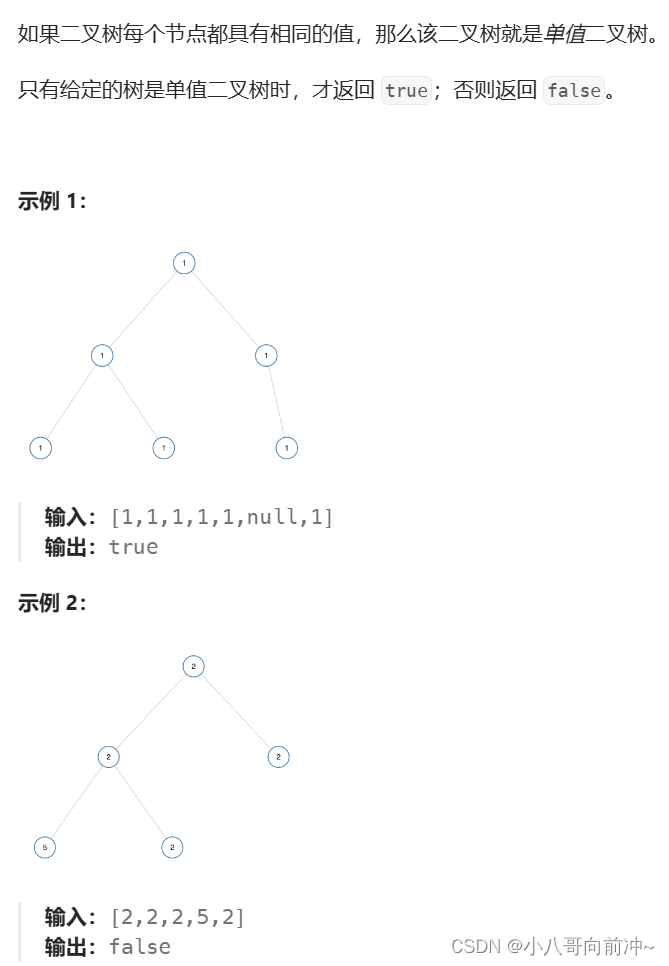
详情：单值二叉树_LeetCode

思路：

运用递归，每次递归将根，左孩子，右孩子进行比较！

而最后一次就是左子树，右子树和根的比较！

代码：

bool isUnivalTree(struct TreeNode* root) {
    //递归
    //每次递归看成根，左孩子，右孩子比较
    //最后一次递归是左子树和右子树和根比较
    if(root==NULL)
       return true;
    //左子孩子存在就开始比较
    if(root->left&&root->val!=root->left->val)
        return false;
    //右孩子存在就开始比较
    if(root->right&&root->val!=root->right->val)
        return false;
    return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

对称二叉树

题目：

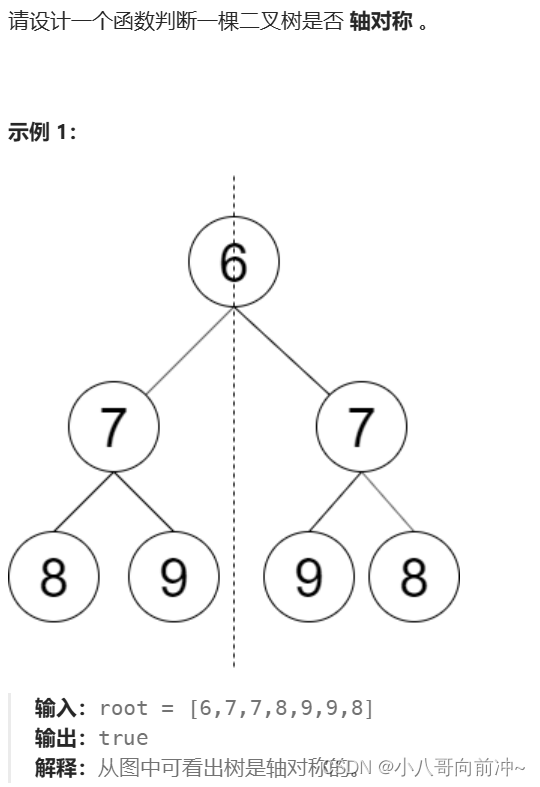
详情：判断对称二叉树_LeetCode

思路：

运用递归，将左子树和右子树进行比较！

所以需要分装一个函数比较左子树和右子树。

这个函数里面的左子树的左孩子要和右子树的右孩子比较，左子树的右孩子要和右子树的左孩子比较！

图：

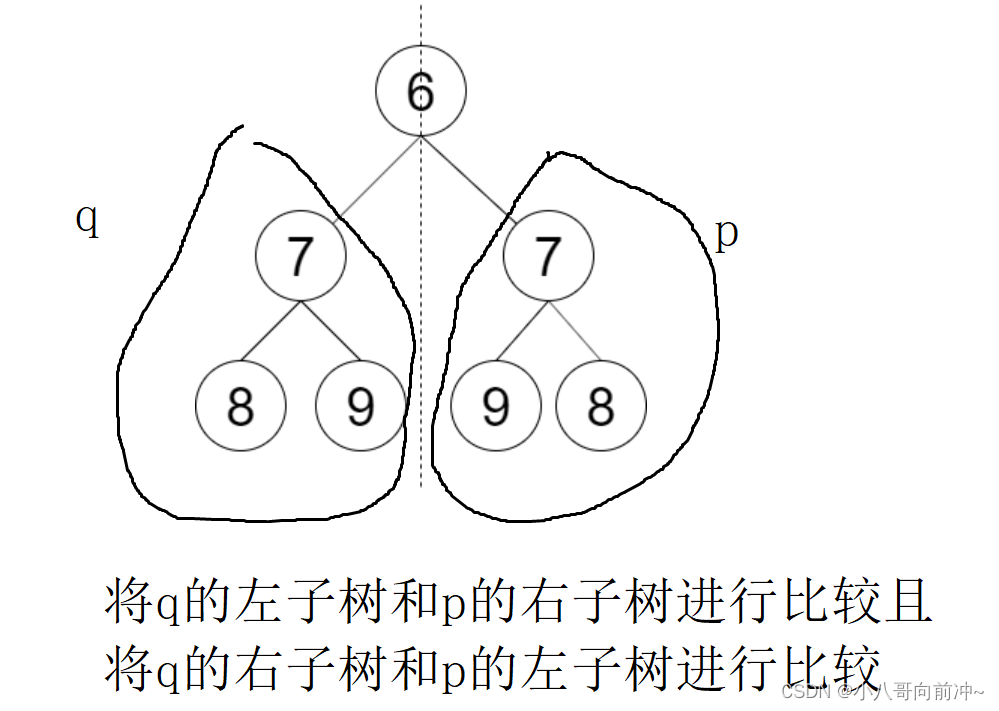
代码：

bool _checkSymmetricTree(struct TreeNode*q,struct TreeNode*p)
{
    //递归
    //最后一次递归是q的左子树和p的右子树判断，q的右子树和p的左子树判断
    //每次递归看作q的根和p的根判断，q的孩子和p的孩子判断是否相等
    if(q==NULL&&p==NULL)
        return true;
    //如果俩根只有一个为空就是假
    if(q==NULL||p==NULL)
        return false;
    if(q->val!=p->val)
        return false;
    return _checkSymmetricTree(q->left,p->right)&&
           _checkSymmetricTree(q->right,p->left);
}
bool checkSymmetricTree(struct TreeNode* root) {
    //递归
    //最后一次递归是左子树和右子树是否相等
    if(root==NULL)
       return true;
    return _checkSymmetricTree(root->left,root->right);
}

计算二叉树的深度

题目：

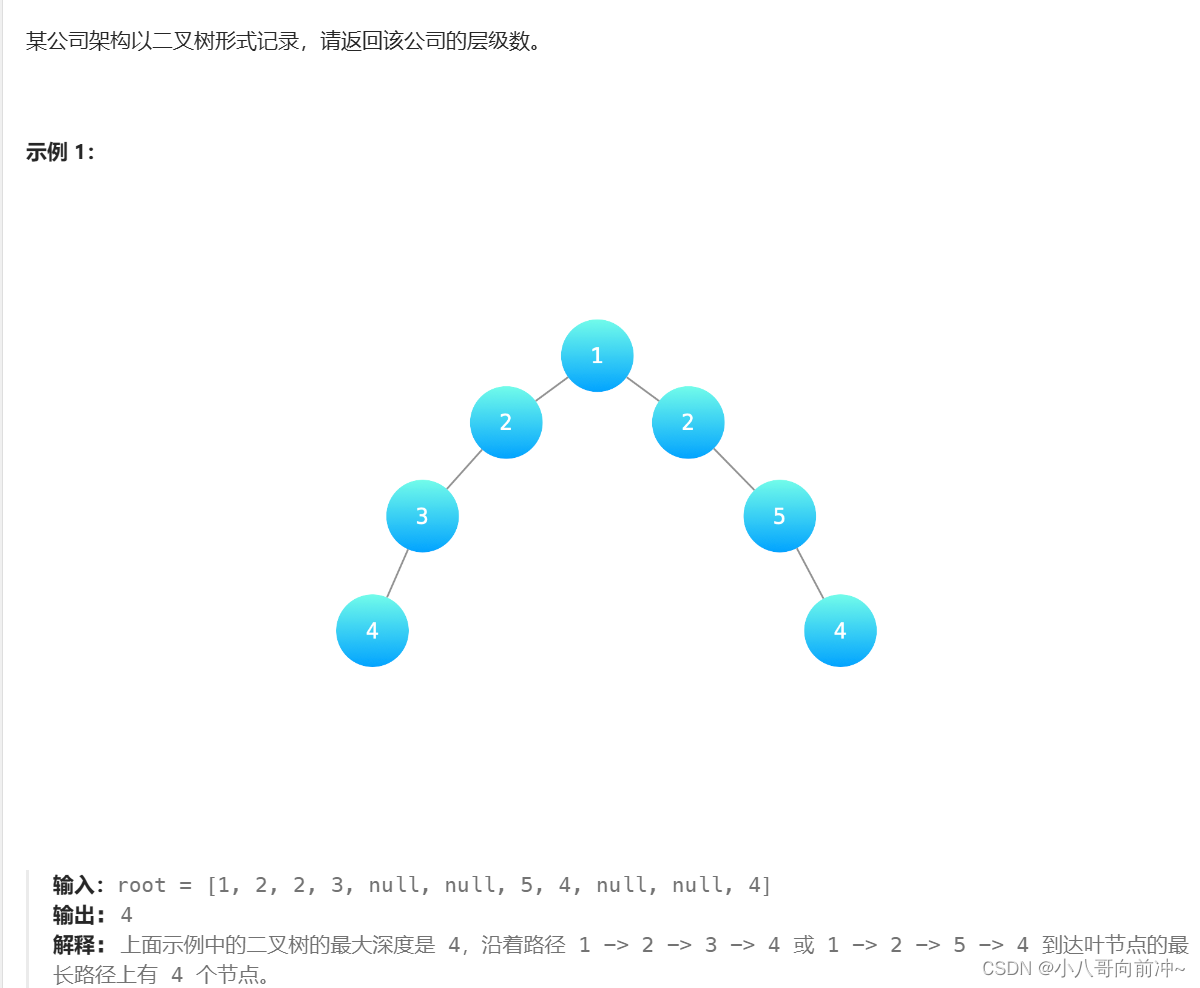
详情：计算二叉树深度_LeetCode

思路：

我们不难看出：树的高度==高的子树的高度+1。

代码：

int calculateDepth(struct TreeNode* root) {
    //左子树和右子树比较，大的子树加+1就是高度
    if(root==NULL)
         return 0;
    int leftheight=calculateDepth(root->left);
    int rightheight=calculateDepth(root->right);
    return leftheight>rightheight?leftheight+1:rightheight+1;
}

二叉树的前序遍历

题目：

前序遍历二叉树，将值存到数组中。

详情：二叉树的前序遍历_LeetCode

思路：

为了开辟的数组不大不小，我们计算树节点总数，然后进行前序遍历一个一个将树节点数值写入数组中。

以此则中序遍历和后序遍历也是如此！

代码：

int TreeSize(struct TreeNode*root)
{
    //左子树节点+右子树节点+1
    return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
}
void preorder(struct TreeNode*root,int*a,int*i)
{
    if(root==NULL)
      return;
    a[(*i)++]=root->val;
    preorder(root->left,a,i);
    preorder(root->right,a,i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    //为了开辟的数组不大不小，我们先计算树的节点总数
    *returnSize=TreeSize(root);
    int*a=(int*)malloc(sizeof(int)*(*returnSize));
    int i=0;
    preorder(root,a,&i);
    return a;
}

相同二叉树

题目：

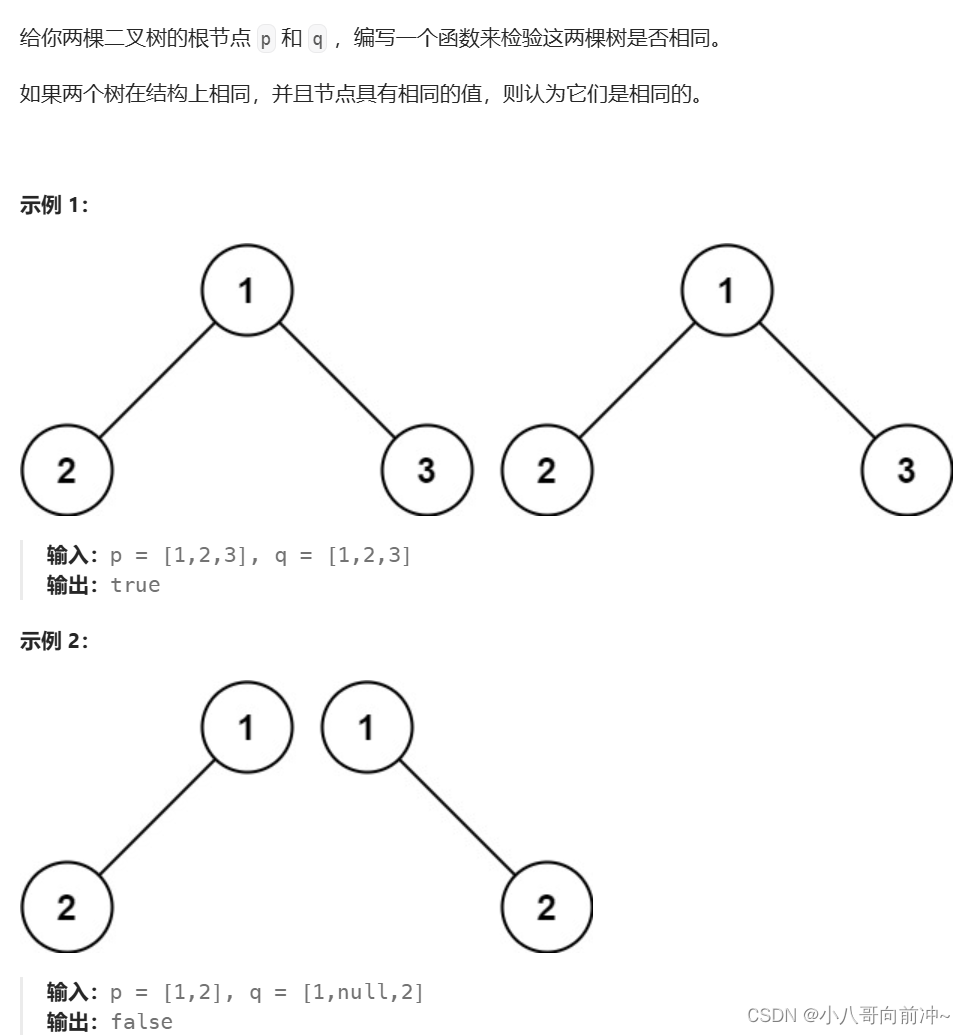
详情：相同的树_LeetCode

思路：

运用递归，分别将俩棵树的根和根比较，左子树和左子树比较，右子树和右子树比较！

图：

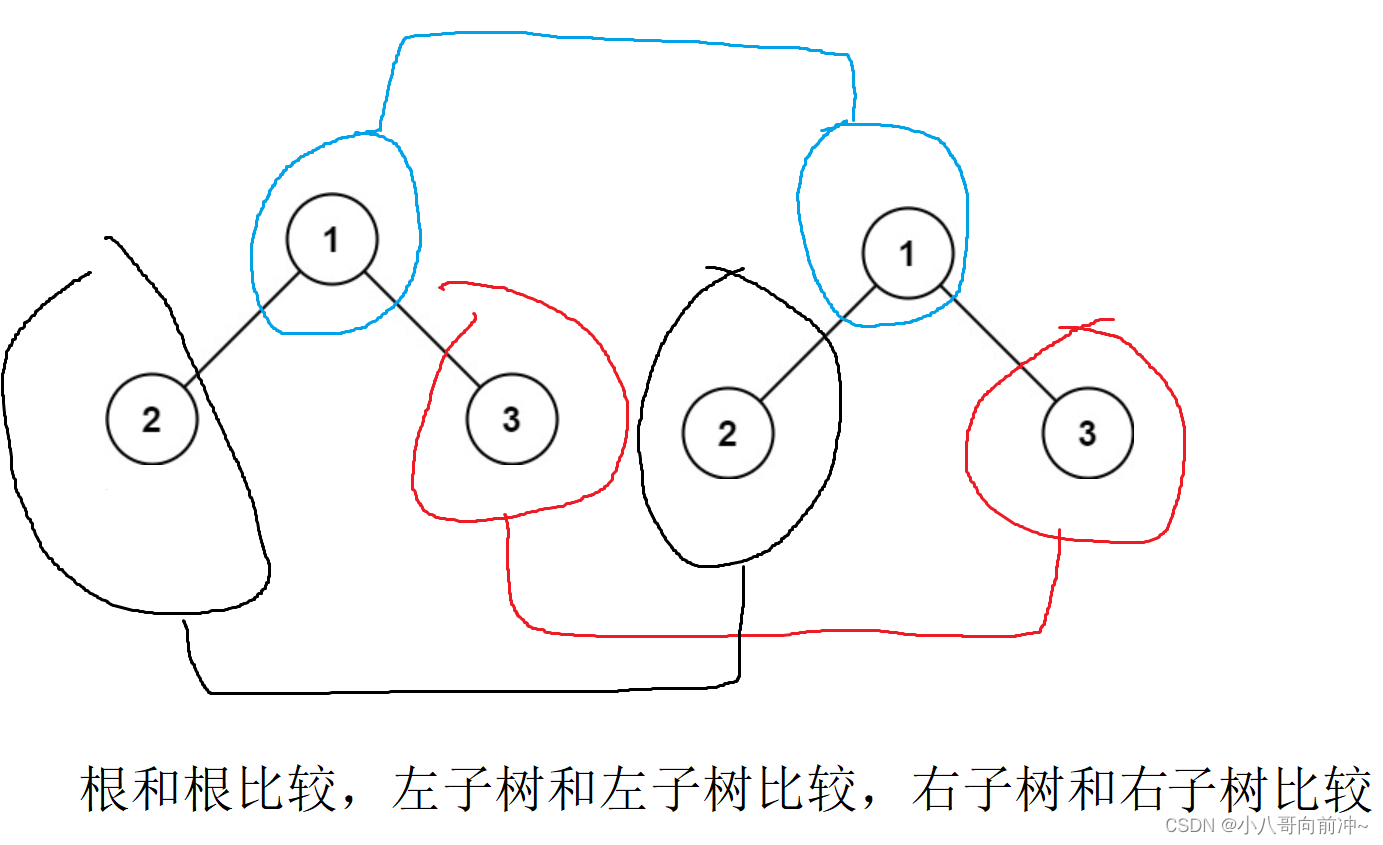
代码：

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    //p的左子树和q的左子树比较，p的右子树和q的右子树比较
    if(p==NULL&&q==NULL)
       return true;
    if(p==NULL||q==NULL)
       return false;
    if(p->val!=q->val)
       return false;
    return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);    
}

另一棵树的子树

题目：

详情：另一颗子树_LeetCode

思路：

将树的所有子树和另一棵树进行比较，如果相同就真，否则，假！

将问题转化成俩棵树是否相同的比较！

代码：

bool SameTree(struct TreeNode*q,struct TreeNode*p)
{
    if(q==NULL&&p==NULL)
       return true;
    if(q==NULL||p==NULL)
        return false;
    if(q->val!=p->val)
        return false;
    return SameTree(q->left,p->left)&&SameTree(q->right,p->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
    //找出所有子树，再和另一棵子树比较是否相同
    if(root==NULL)
      return false;
    //值相等时，开始比较树是否相等
    if(root->val==subRoot->val&&SameTree(root,subRoot))
       return true;
    //在左子树和右子树中能找到就行
    return isSubtree(root->left,subRoot)
    ||isSubtree(root->right,subRoot);
}

二叉树的构建和遍历

题目：

详情：二叉树的构建和遍历_牛客网

思路：

遍历读取数组的每个值，前序遍历将树建好，最后中序遍历二叉树打印！

代码：

#include <stdio.h>
#include<stdlib.h>
typedef struct TreeNode {
    struct TreeNode* left;
    struct TreeNode* right;
    char val;
} TNode;
void Inoder(TNode*root)
{
    if(root==NULL)
       return;
    Inoder(root->left);
    printf("%c ",root->val);
    Inoder(root->right);
}
TNode*CreateTree(char*a,int*i)
{
    if(a[(*i)]=='#')
    {
        (*i)++;
        return NULL;
    }
    TNode*node=(TNode*)malloc(sizeof(TNode));
    node->val=a[(*i)++];
    node->left=CreateTree(a, i);
    node->right=CreateTree(a, i);
    return node;
}
int main() {
    char a[100];
    scanf("%s",a);
    int i=0;
    TNode*root=CreateTree(a,&i);
    Inoder(root);
    return 0;
}

翻转二叉树

题目：

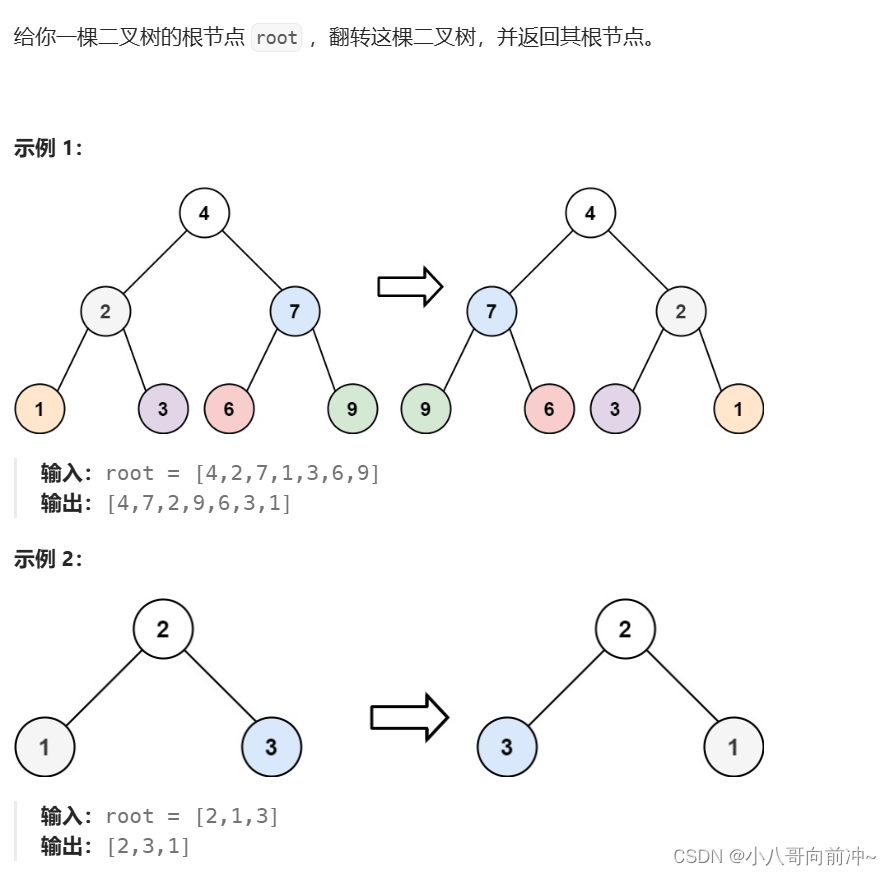
详情：翻转二叉树_LeetCode

思路：

递归，先将左子树交换，再将右子树交换！

代码：

struct TreeNode* invertTree(struct TreeNode* root) {
    if(root==NULL)
       return NULL;
    struct TreeNode*tmp;
    tmp=root->left;
    root->left=root->right;
    root->right=tmp;
    //交换左子树
    if(root->left)
      invertTree(root->left);
    //交换右子树
    if(root->right)
      invertTree(root->right);
    return root;
}

判断平衡二叉树

题目：

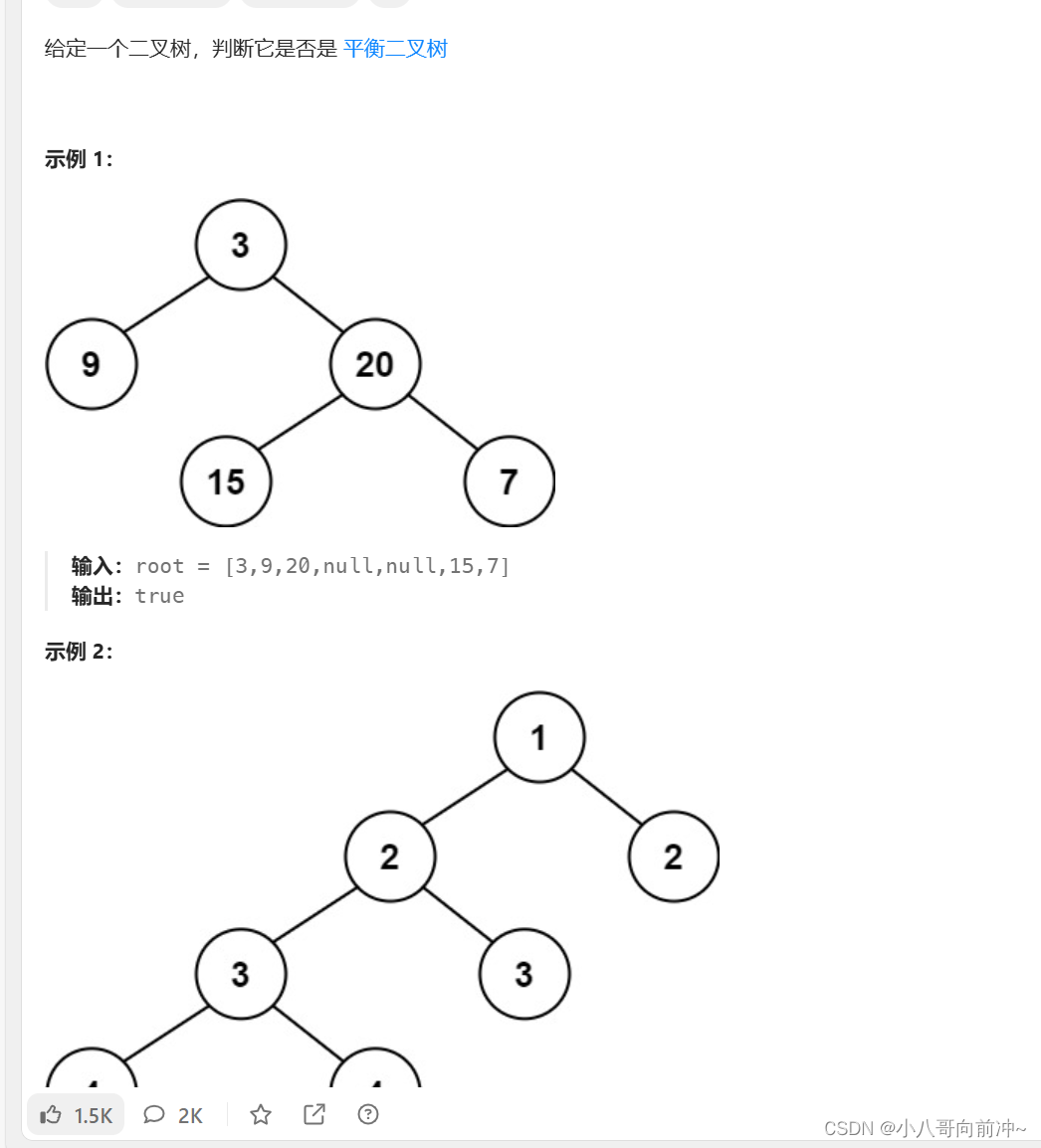
详情：平衡二叉树_LeetCode

代码：

int TreeHeight(struct TreeNode* p) {
    if (p == NULL)
        return 0;
    int leftheight = TreeHeight(p->left);
    int rightheight = TreeHeight(p->right);
    return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
}
bool isBalanced(struct TreeNode* root) {
    if (root == NULL)
        return true;
    return isBalanced(root->left) && isBalanced(root->right)&&
    abs(TreeHeight(root->left) - TreeHeight(root->right)) <= 1;
}

今天的题目，你都学会了吗？我们下期见！