只要系统形成 E_best = max(bw / delay) 共识，系统就是稳定的。

设两条流 f1，f2 共享瓶颈链路，用 cwnd 约束 inflight，其 cwnd 分别为 x，y，用简单的微分方程建模：

$\frac{dx}{dt}=c-b\ast x-a\ast y$
$\frac{dy}{dt}=c-b\ast y-a\ast x$

其中，c 是自我激励强度参数，b 是自我抑制强度参数，c 是相互抑制强度参数。b，c 共同决定了抑制行为，是 E_best 共识的决定性参数，是为 “适可而止”。

f1 自我约束，f2 增加了 f1 的约束，反之亦然。

试求上述系统的稳定点，然后分析其相空间的系统轨线，令：

$\frac{dx}{dt}=c-b\ast x-a\ast y=0$
$\frac{dy}{dt}=c-b\ast y-a\ast x=0$

则获得两条直线，其交点即稳定点：

Lf1：$y=f(x)=-\frac{b}{a}x+\frac{c}{a}$

Lf2：$y=g(x)=-\frac{a}{b}x+\frac{c}{b}$

两条直线相交于相空间第一象限 P 点，将其分为了 4 个空间 A，B，C，D：

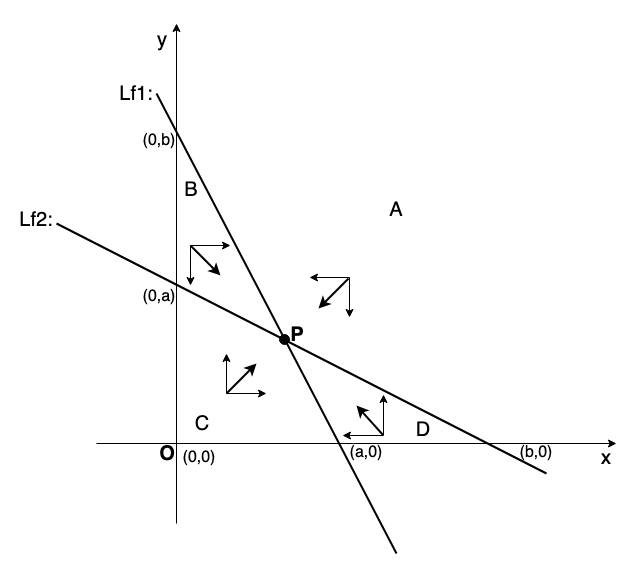
在区域 A，$y＞f(x)$，$y＞g(x)$，因此 $\frac{dx}{dt}＜0$，$\frac{dy}{dt}＜0$，轨迹向稳定点 P 收敛。同理，在区域 B，C，D，根据 y 的位置和 dx/dt，dy/dt 的符号亦可推出轨迹向 P 收敛，如上图剪头所示。

其实上述系统模型就是 Lotka-Volterra 系统的简化变体，这种简化的线性渐进假设比三次 logistic 渐进系统更符合 inflight 守恒拥塞控制算法。

inflight 守恒算法并不关注自我激励的细节，它可以是加性增 cwnd，也可以是乘性增 cwnd，甚至可以是指数增 cwnd，因此我将其简化为线性激励，即 $\frac{dx}{dy}=c$，算法更关注的是自我抑制和互相抑制，这是一类负反馈，用 $\frac{dx}{dy}=c-d\ast x$ 建模，不同的是，将 d 因子拆分成两部分，就形成了一个耦合系统。

获得这微分方程的解析解很麻烦且不必要，要观测系统行为，数值解就够。以下是模拟数值，分三组参数，a，b，c 分别为 (0.4, 0.5, 2), (0.6, 1.5, 3), (2, 3, 1.5), (1, 2, 3)：

import numpy as np
import matplotlib.pyplot as plt

# 定义参数和初始条件：确保 a < b，要让自我抑制占主导
params_sets = [(0.4, 0.5, 2), (0.6, 1.5, 3), (2, 3, 1.5), (1, 2, 3)]
x0, y0 = 1, 0
T, dt = 30, 0.1
times = np.arange(0, T+dt, dt)

# 绘制图形
plt.figure(figsize=(12, 6))

for i, (a, b, c) in enumerate(params_sets, start=1):
    # 使用欧拉方法求解
    x = np.zeros_like(times)
    y = np.zeros_like(times)
    x[0], y[0] = x0, y0
    for n in range(1, len(times)):
        x[n] = x[n-1] + dt * (c - b*x[n-1] - a*y[n-1])
        y[n] = y[n-1] + dt * (c - b*y[n-1] - a*x[n-1])
    
    plt.subplot(1, 4, i)
    plt.plot(times, x, label='x(t)')
    plt.plot(times, y, label='y(t)', linestyle='--')
    plt.title(f'a={a}, b={b}, c={c}')
    plt.xlabel('Time (t)')
    plt.ylabel('Population')
    plt.legend()
    plt.grid(True)

plt.tight_layout()
plt.show()

结果如下：

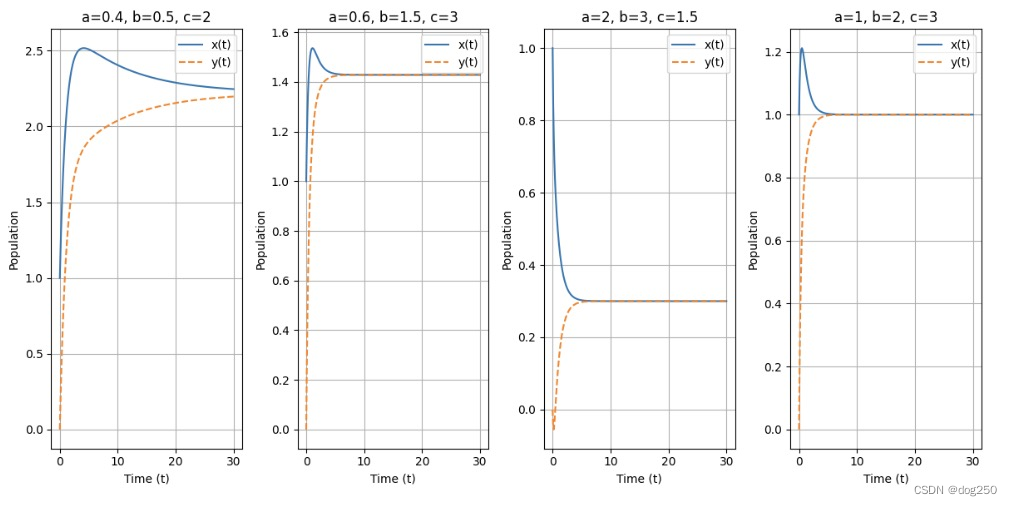
确保 a < b，并且不相差太大是关键，这是流量共存收敛的关键，这也是为什么我在 inflight 守恒算法中引入携带两个负反馈余量的原因，以确保系统：

• 稳定平衡，不会跑飞；
• 对冲差异，快速收敛。

浙江温州皮鞋湿，下雨进水不会胖。