一.右单旋

新节点插入较高左子树的左侧—左左：右单旋

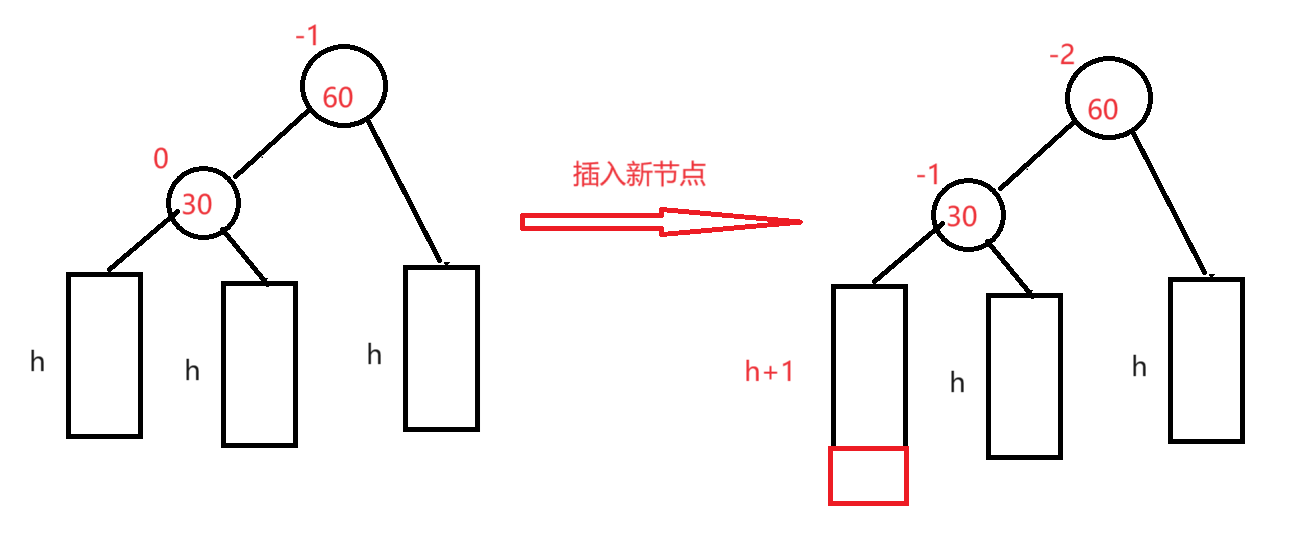
由于在较高左子树的左侧插入一个节点后，左边插入导致30的平衡因子更新为-1，而60平衡因子更新为-2，此时不平衡，引发旋转，右旋解决问题：看下图
：

将60进行一次右单旋后，30和60的平衡因子都更新为了0，此时AVL树重新平衡，更新结束。

代码实现：

void RotateR(Node* parent)
		{
			Node* subL = parent->_left;
			Node* subLR = subL->_right;
			parent->_left = subLR;
			if(subLR)
				subLR->_parent = parent;
			subL->_right = parent;
			Node* ppnode = parent->_parent;
			parent->_parent = subL;
			if (parent == _root)
			{
				_root = subL;
				subL->_parent = nullptr;
			}
			else
			{
				if (parent == ppnode->_left)
				{
					ppnode->_left = subL;
				}
				else
				{
					ppnode->_right = subL;
				}
				subL->_parent = ppnode;
			}
			parent->_bf = 0;
			subL->_bf = 0;
		}

二. 左单旋

新节点插入较高右子树的右侧—右右：左单旋

由于在较高右子树的右侧插入一个节点后，右边插入导致30的平衡因子更新为1，而60平衡因子更新为2，此时不平衡，引发旋转，左旋解决问题：看下图
：

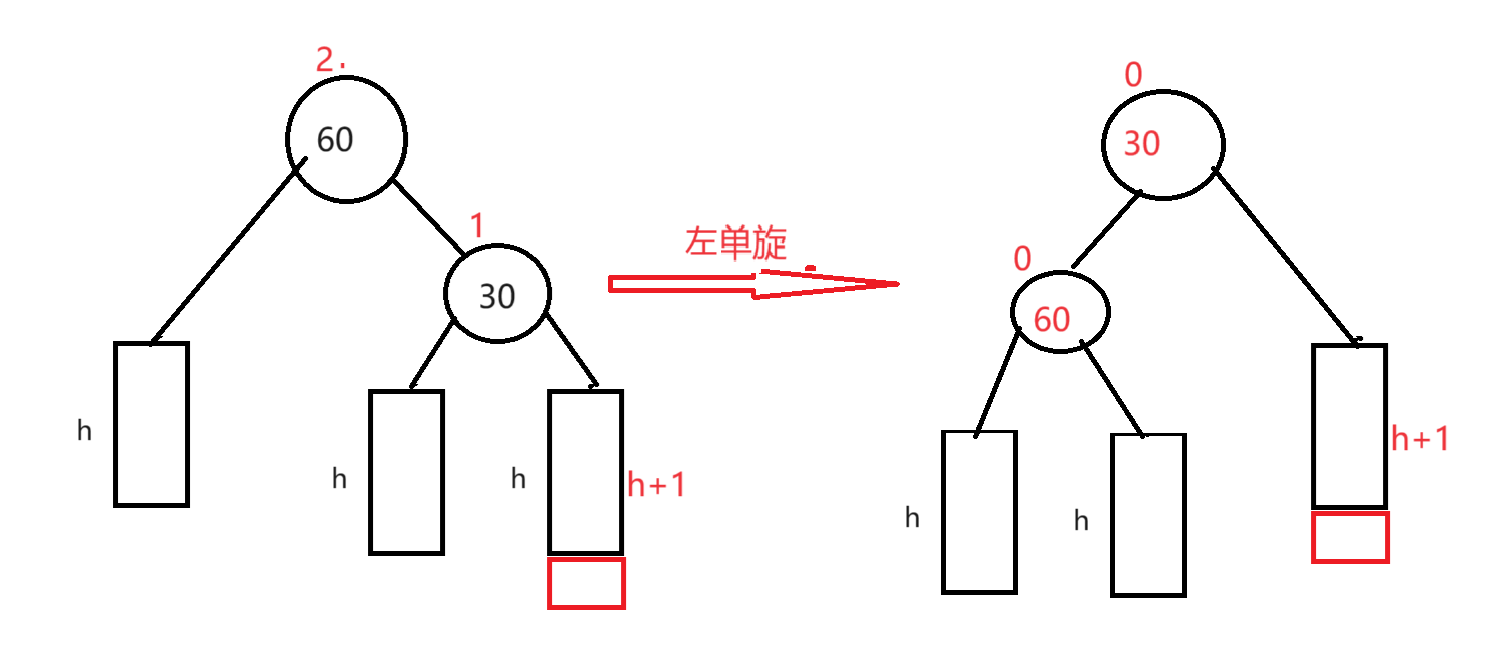
将60进行一次左单旋后，30和60的平衡因子都更新为了0，此时AVL树重新平衡，更新结束。
代码实现：

void RotateL(Node* parent)
		{
			Node* subR = parent->_right;
			Node* subRL = subR->_left;
			parent->_right = subRL;
			if (subRL)
				subRL->_parent = parent;
			subR->_left = parent;
			Node* ppnode = parent->_parent;
			parent->_parent = subR;
			if (_root == parent)
			{
				_root = subR;
				subR->_parent = nullptr;
			}
			else
			{
				if (parent == ppnode->_left)
				{
					ppnode->_left = subR;
				}
				else
				{
					ppnode->_right = subR;
				}
				subR->_parent = ppnode;
			}
			parent->_bf = 0;
			subR->_bf = 0;
		}

三. 右左双旋

新节点插入较高右子树的左侧—右左：先右单旋再左单旋
此时进行右左双旋分为三种情况：
情况一：h==0
插入新结点后，60自己就是新增节点

此时先将60进行右旋

再将30进行左旋

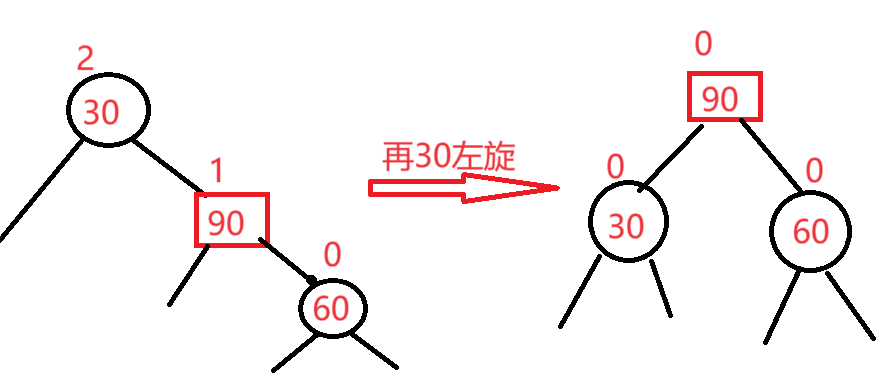
情况二：h>0，在c插入(这里以h2为例）
同上理旋转：

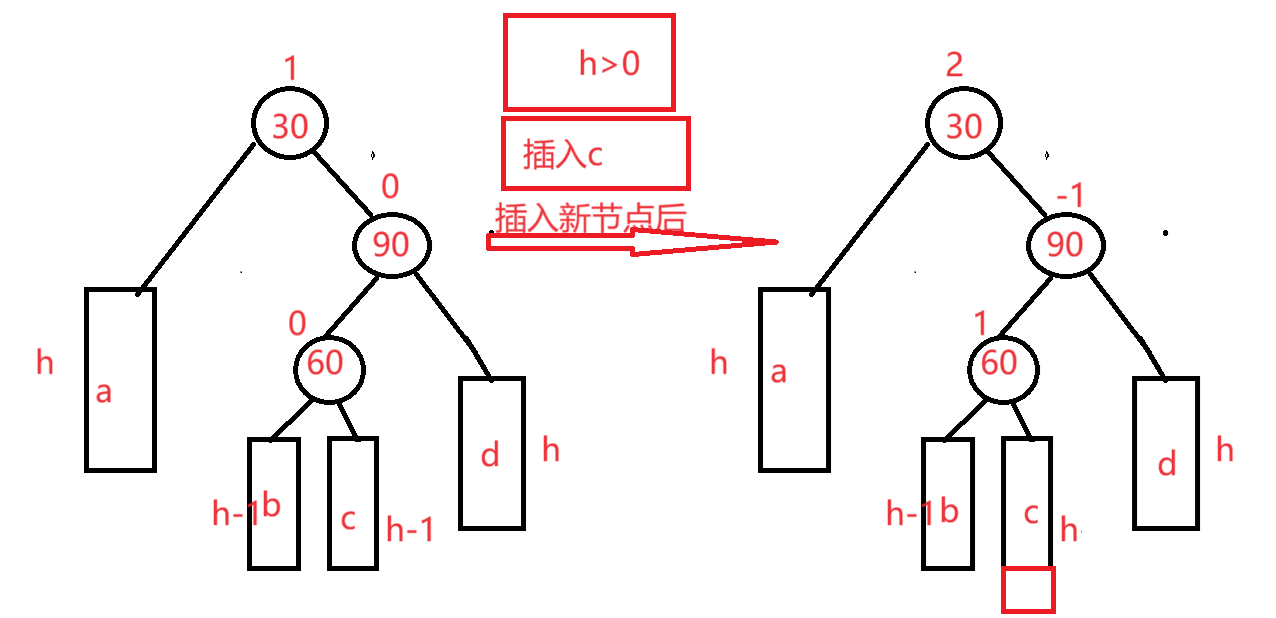
先90进行右旋

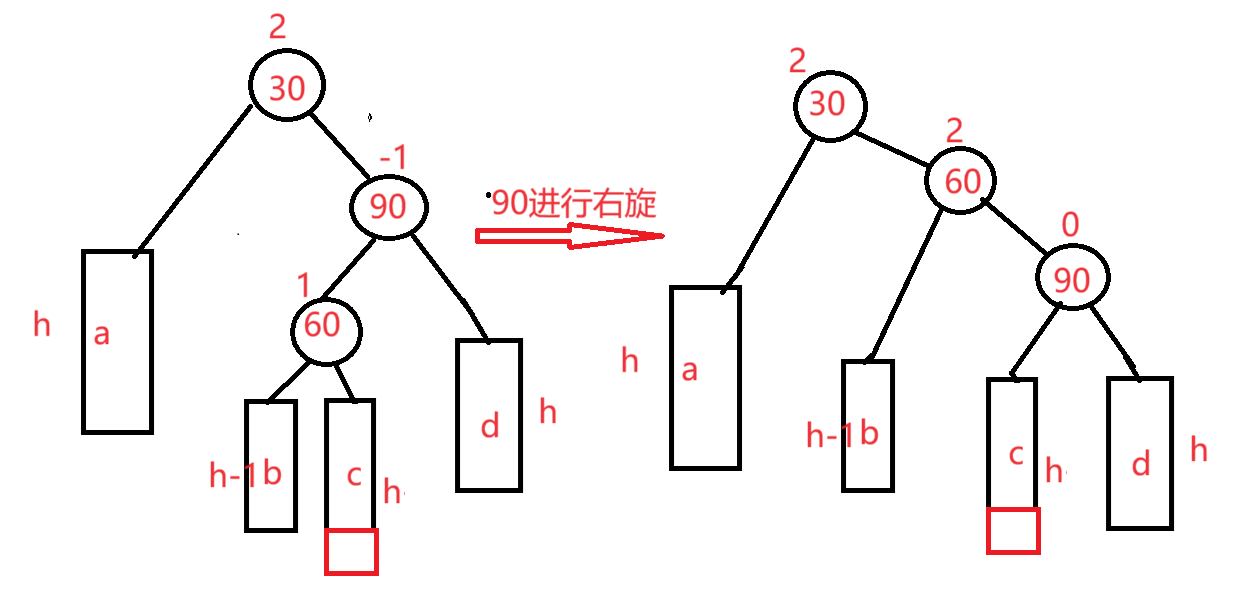
最后30进行左旋

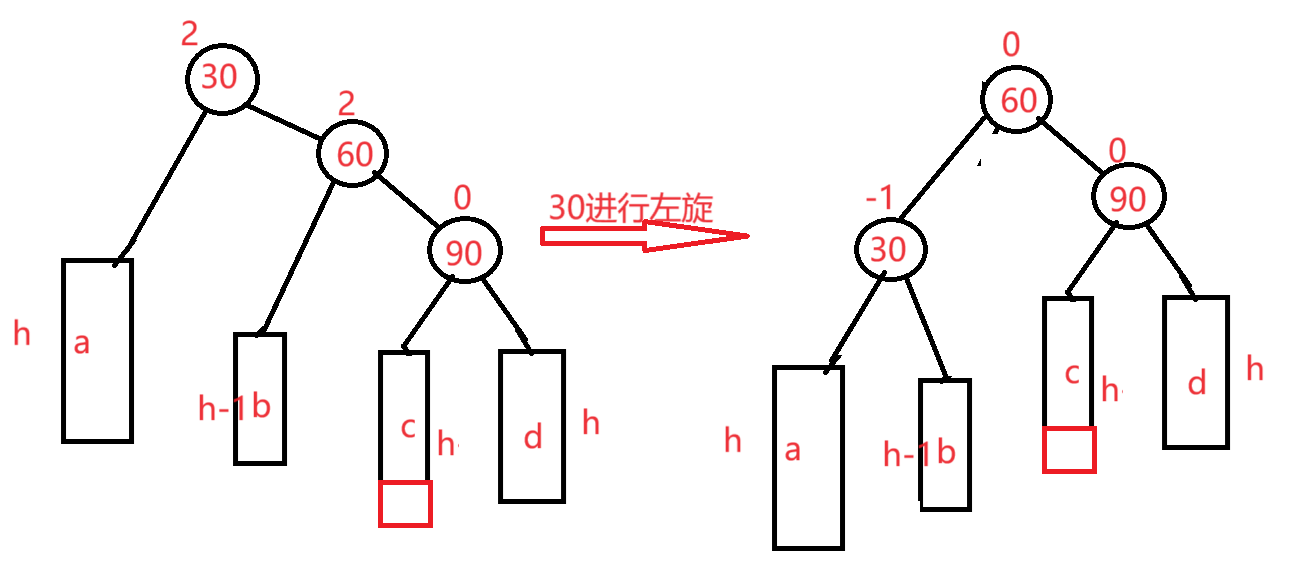
情况三：h>0，在b插入(这里以h2为例）

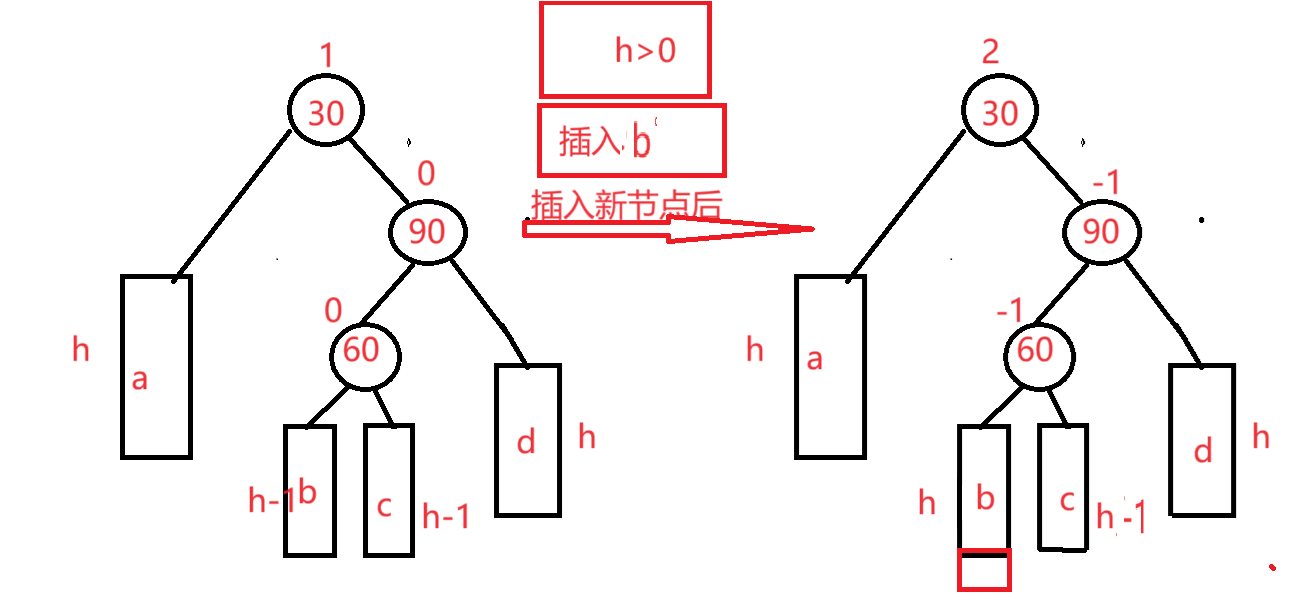
先将90进行右旋

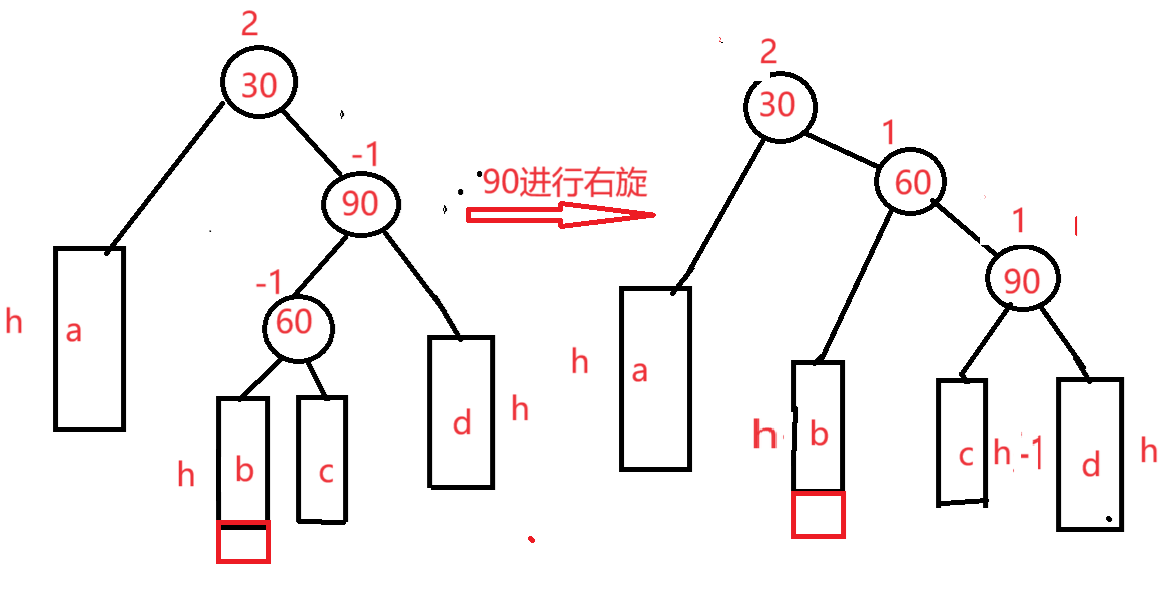
再将30进行左旋

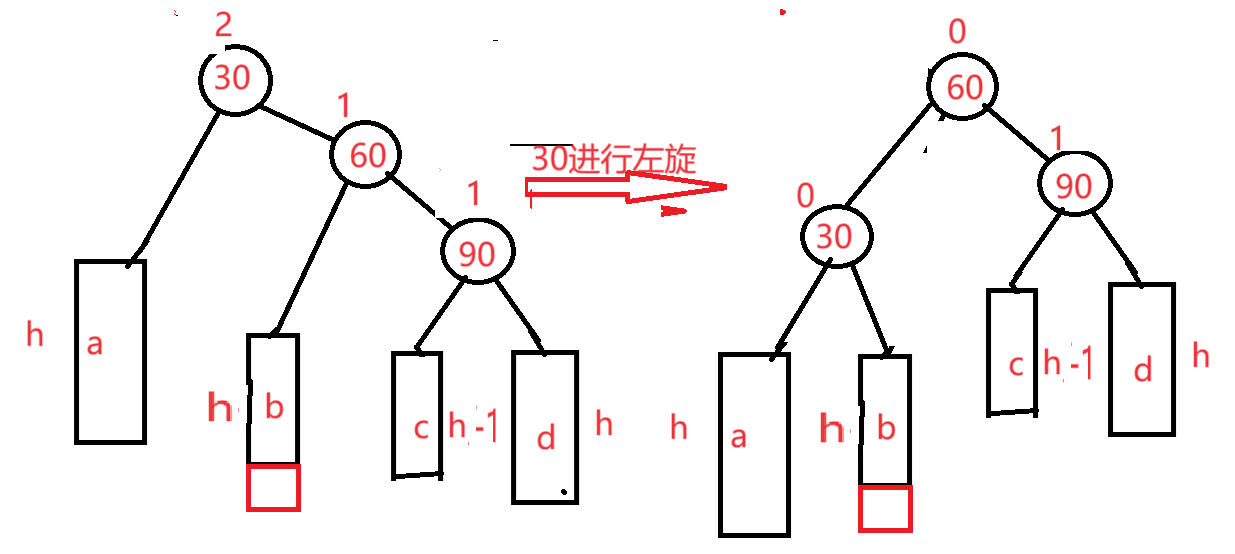
右左双旋代码实现：

void RotateRL(Node* parent)
		{
			Node* subR = parent->_right;
			Node* subRL = parent->_left;
			int bf = subRL->_bf;
			RotateLR(subR);
			RotateL(parent);
			subRL->_bf = 0;
			if (bf == -1)
			{
				subR->_bf = 1;
				parent->_bf = 0;
			}
			else if (bf == 1)
			{
				subR->_bf = 0;
				parent->_bf = -1;
			}
			else if (bf == 0)
			{
				subR->_bf = 0;
				parent->_bf = 0;
			}
			else
			{
				assert(false);
			}
		}

四. 左右双旋

新节点插入较高左子树的右侧—左右：先左单旋再右单旋
此时进行左右双旋分为三种情况：
情况一：h==0
插入新结点后，60自己就是新增节点

30进行左旋

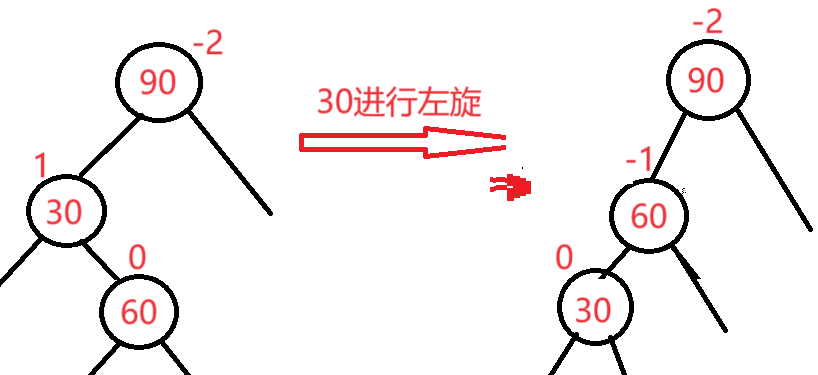
90进行右旋

情况二：h>0，在c插入(这里以h2为例）

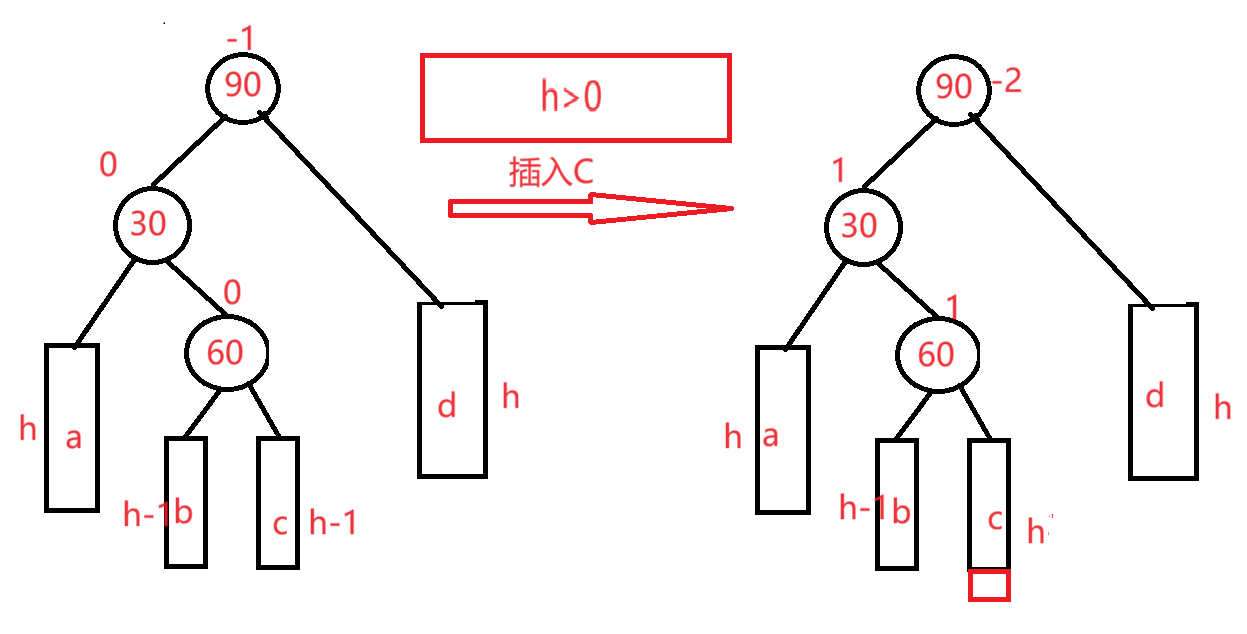
30进行左旋

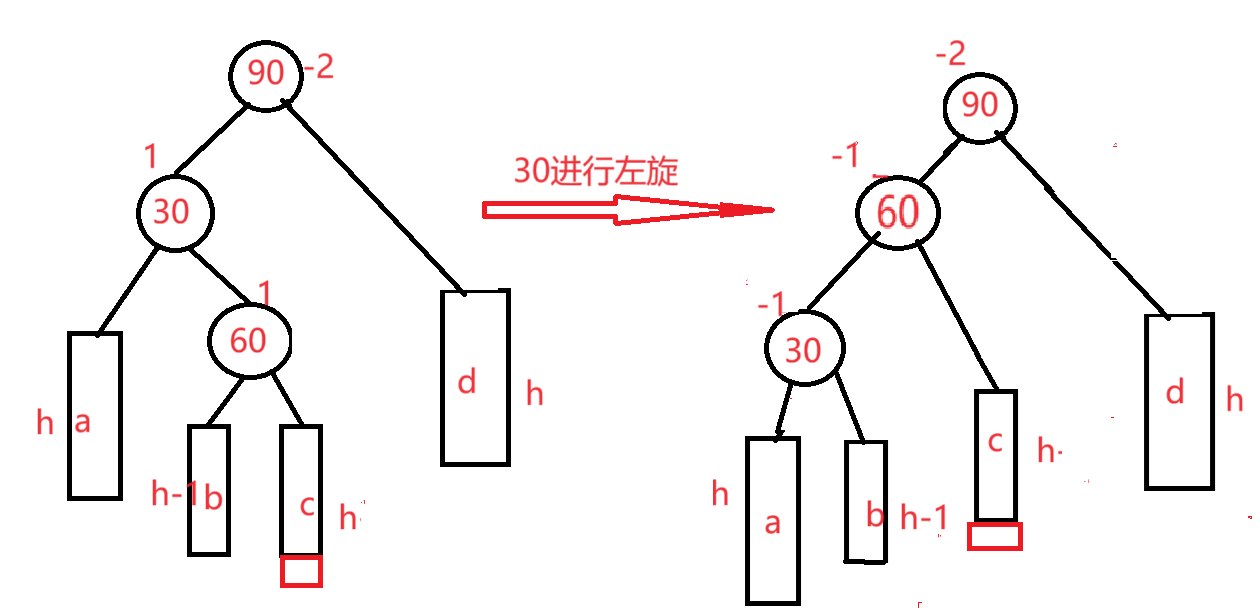
90进行右旋

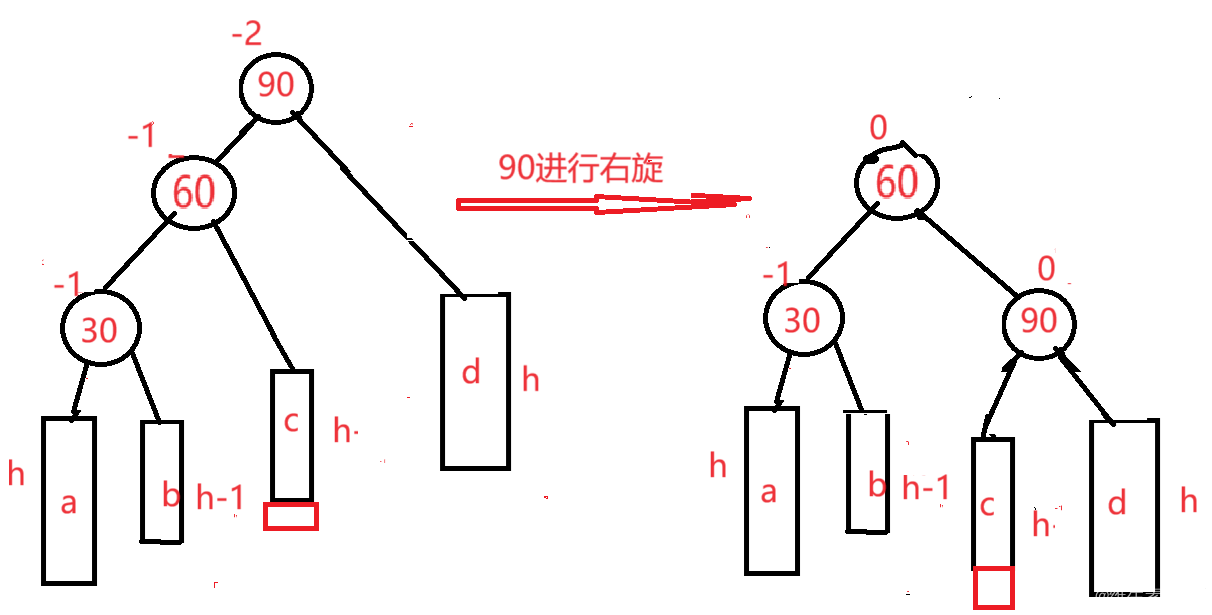
情况三：h>0，在b插入(这里以h2为例）

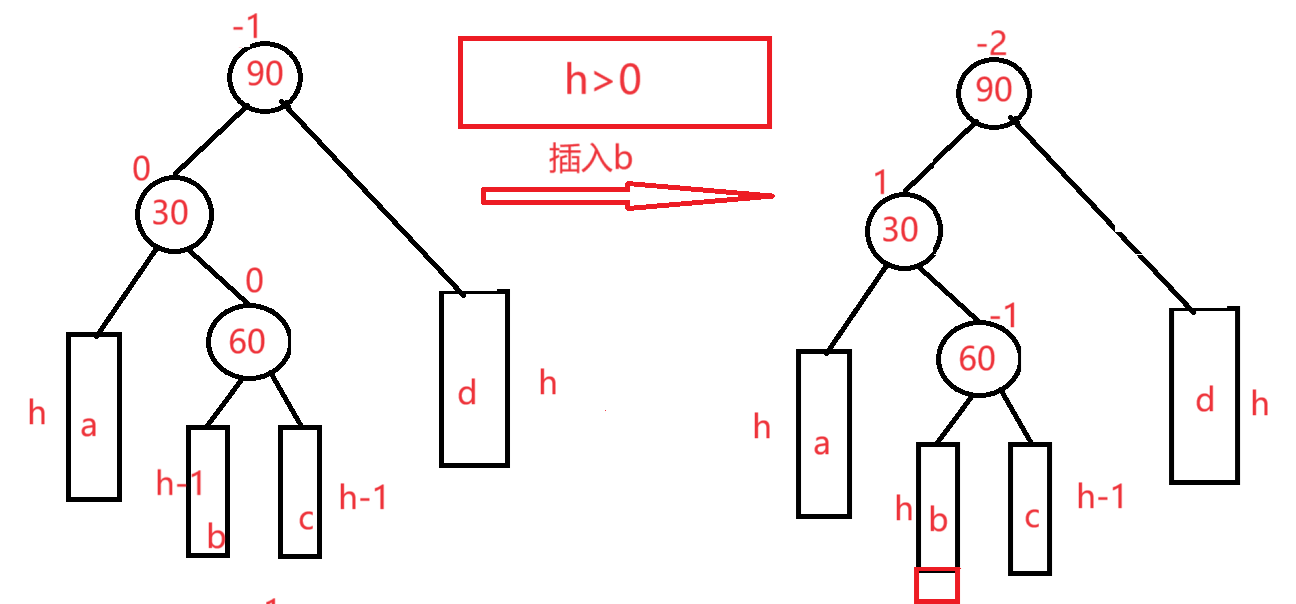
30进行左旋

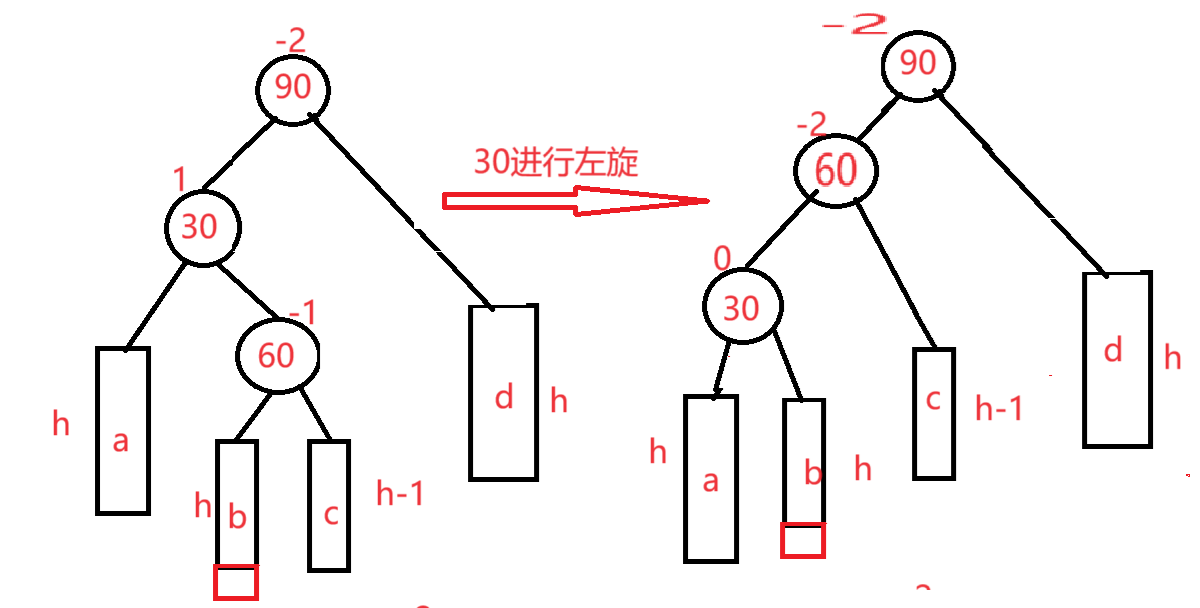
90进行右旋

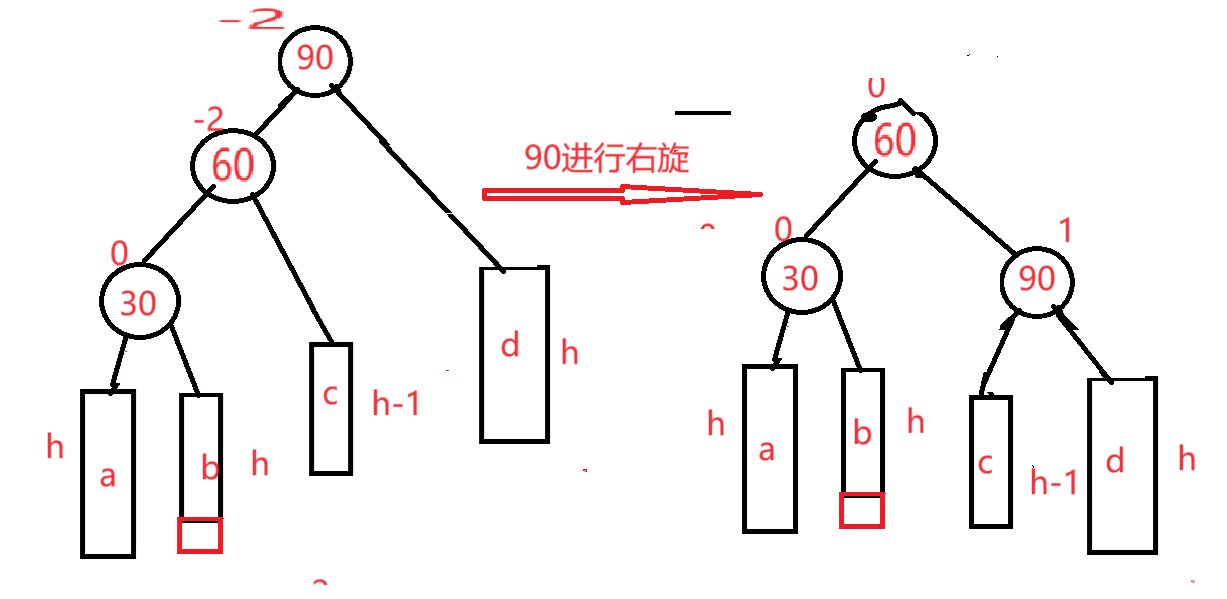
左右双旋代码实现：

void RotateLR(Node* parent)
		{
			Node* subL = parent->_left;
			Node* subLR = subL->_right;
			int bf = subLR->_bf;
			RotateL(subL);
			RotateR(parent);
			subLR->_bf = 0;
			if (bf == 0)
			{
				subL->_bf = 0;
				parent->_bf = 0;
			}
			else if (bf == 1)
			{
				subL->_bf = -1;
				parent->_bf = 0;
			}
			else if (bf == -1)
			{
				subL->_bf = 0;
				parent->_bf = 1;
			}
			else
			{
				assert(false);
			}
		}

**总结：1.对于单旋，旋转之后就平衡了，结束 2.对于双旋，旋转之后也平衡了，但此时要更新平衡因子，怎么更新取决于更新前代码中subL的平衡因子，
分三种情况，具体看代码实现。