矩阵链相乘（动态规划法）

news2024/11/8 6:31:00

问题分析

矩阵链相乘问题是一个经典的动态规划问题。给定一系列矩阵，目标是找到一种最优的乘法顺序，使得所有矩阵相乘所需的标量乘法次数最少。矩阵链相乘问题的关键在于利用动态规划来避免重复计算子问题。

算法设计

定义子问题：设 𝑤[𝑖,𝑗]表示计算矩阵 𝐴𝑖 到 𝐴𝑗的最小乘法次数。
递归关系：根据递归关系式：
其中 𝑝 是矩阵的维度数组，𝑝𝑖表示第 𝑖个矩阵的行数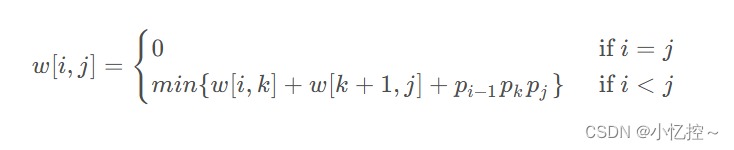， $p_{i+1}$ 表示第 𝑖个矩阵的列数。
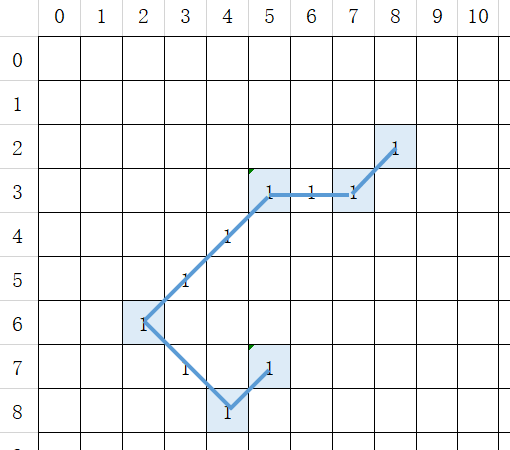
w[i,j] 表示第 i个矩阵到第 j个矩阵，路径上的矩阵链的最小代价
$p_{i-1}p_{k}p_{j}$ 代表从最优子解向它的最优父解构造时需要的代价
边界条件：当 𝑖=𝑗 时，𝑤[𝑖,𝑗]=0，因为单个矩阵不需要乘法。
计算顺序：从小规模问题开始，逐步计算较大规模问题。

其他的情况以此类推.....

伪代码

function MatrixChainOrder(p):
    n = length(p) - 1
    let w be a 2D array of size n x n
    for i = 1 to n:
        w[i, i] = 0
    for l = 2 to n:  // l is the chain length
        for i = 1 to n - l + 1:
            j = i + l - 1
            w[i, j] = infinity
            for k = i to j - 1:
                q = w[i, k] + w[k + 1, j] + p[i - 1] * p[k] * p[j]
                if q < w[i, j]:
                    w[i, j] = q
    return w[1, n]

C实现

#include <stdio.h>
#include <limits.h>

void MatrixChainOrder(int p[], int n) {
    int w[n][n];
    int i, j, k, l, q;

    for (i = 1; i < n; i++)
        w[i][i] = 0;

    for (l = 2; l < n; l++) {
        for (i = 1; i < n - l + 1; i++) {
            j = i + l - 1;
            w[i][j] = INT_MAX;
            for (k = i; k <= j - 1; k++) {
                q = w[i][k] + w[k + 1][j] + p[i - 1] * p[k] * p[j];
                if (q < w[i][j])
                    w[i][j] = q;
            }
        }
    }

    printf("Minimum number of multiplications is %d\n", w[1][n - 1]);
}

int main() {
    int arr[] = {1, 2, 3, 4};
    int size = sizeof(arr) / sizeof(arr[0]);

    MatrixChainOrder(arr, size);

    return 0;
}

结果如下：