✨✨ 欢迎大家来到贝蒂大讲堂✨✨
🎈🎈养成好习惯,先赞后看哦~🎈🎈
所属专栏:数据结构与算法
贝蒂的主页:Betty’s blog
1. 堆排序
1.1. 算法思想
堆排序(Heap Sort)是一种基于堆数据结构的排序算法。其核心思想是将待排序的元素构建成一个最大堆或最小堆,然后依次将堆顶元素与堆中最后一个元素交换,并重新调整堆,使得剩余元素重新满足堆的性质。重复这个过程直到所有元素都被取出,就得到了一个有序的序列。
1.2. 算法步骤
- 建立一个大根堆(升序)。
- 将堆顶元素与堆底末尾元素交换,这时待排序中最大元素成功放到正确的位置,并且将堆中待排序的元素个数
size--。- 然后对堆顶元素进行向下调整,使剩余待排序元素重新形成一个大根堆。
- 重复步骤2,3直至待排序元素个数
size = 1,排序完成。

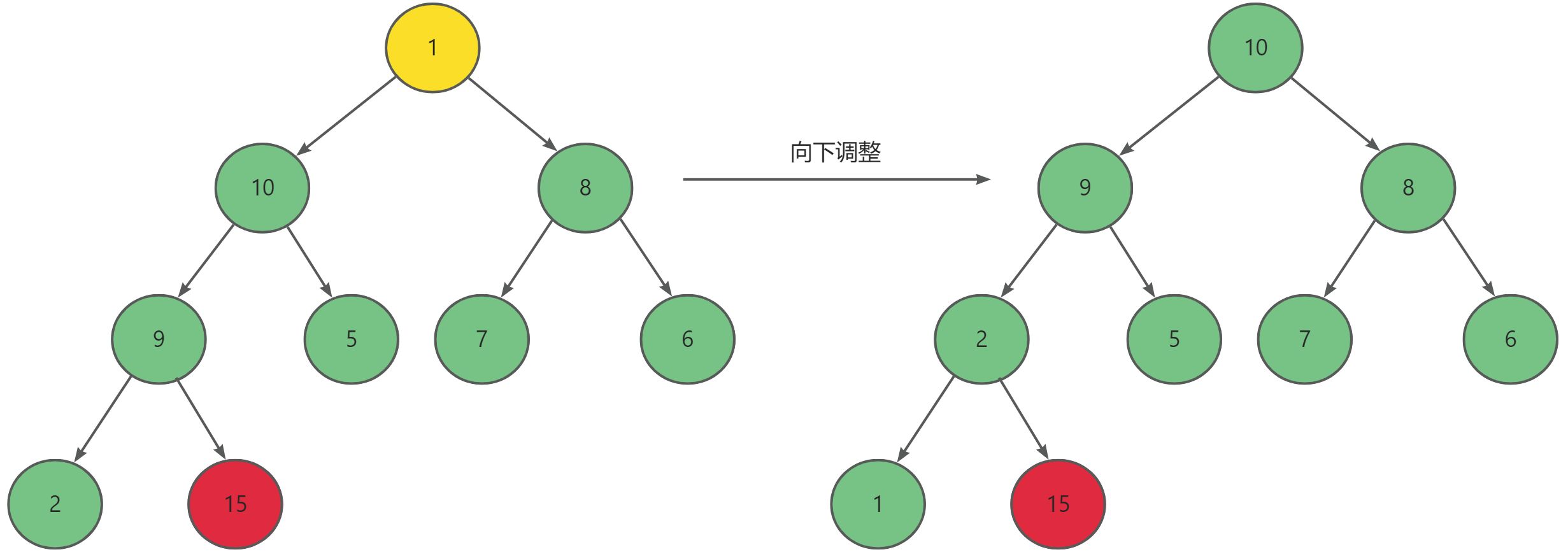
为什么升序要建大堆,降序要建小堆?
因为如果升序一旦建小堆的话,每一个取堆顶的元素之后都可能会破坏原本的堆的结构,都需要重新建堆,而建堆的时间复杂度为O(N),这样N个元素的排序,时间复杂度就会劣化为O(N2 )。
1.3. 动图演示
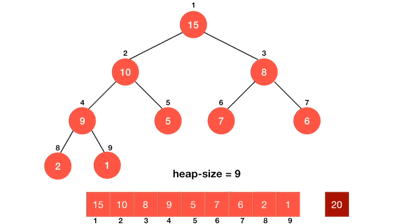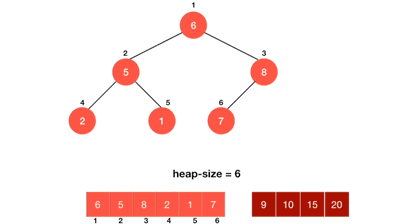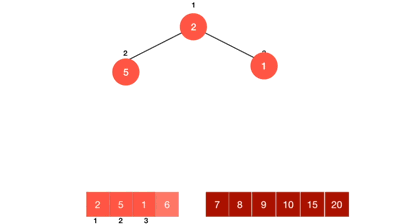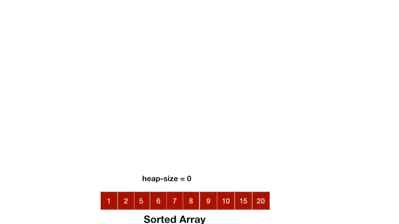
1.4. 代码实现
void AdjustDown(int* arr, int n, int parent)
{
int child = 2 * parent + 1;
while (child < n)
{
if (child + 1 < n && arr[child] < arr[child + 1])
{
child++;
}
if (arr[child] > arr[parent])
{
swap(&arr[child], &arr[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
void HeapSort(int* arr, int n)
{
//向下调整建堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, n, i);
}
int end = n - 1;
while (end > 0)
{
swap(&arr[0], &arr[end]);
AdjustDown(arr, end, 0);
end--;
}
}
1.5. 复杂度分析
- 时间复杂度:向下调整建堆的时间复杂度为O(N),向下调整的时间复杂度为O(logN),一共N次。所以总时间为O(N+NlogN),复杂度为O(NlogN)。
- 空间复杂度:没有开辟额外的空间,所以空间复杂度为O(1)。
2. 计数排序
2.1. 算法思想
**计数排序(Counting Sort)**是一种非比较性的排序算法,适用于一定范围内的整数排序。其核心思想是统计每个元素出现的次数,然后根据这个统计信息,将元素放置到正确的位置上。
2.2. 算法步骤
- 找出待排序数组中的最大值
max和最小值min。- 创建一个长度为
max - min + 1的计数数组count,用于存储每个元素出现的次数。- 遍历待排序数组,统计每个元素出现的次数,将其存储在计数数组中相应的位置上。
- 根据计数数组中的统计信息,将待排序数组重新排列。
- 将排好序的元素从计数数组中放回待排序数组中。
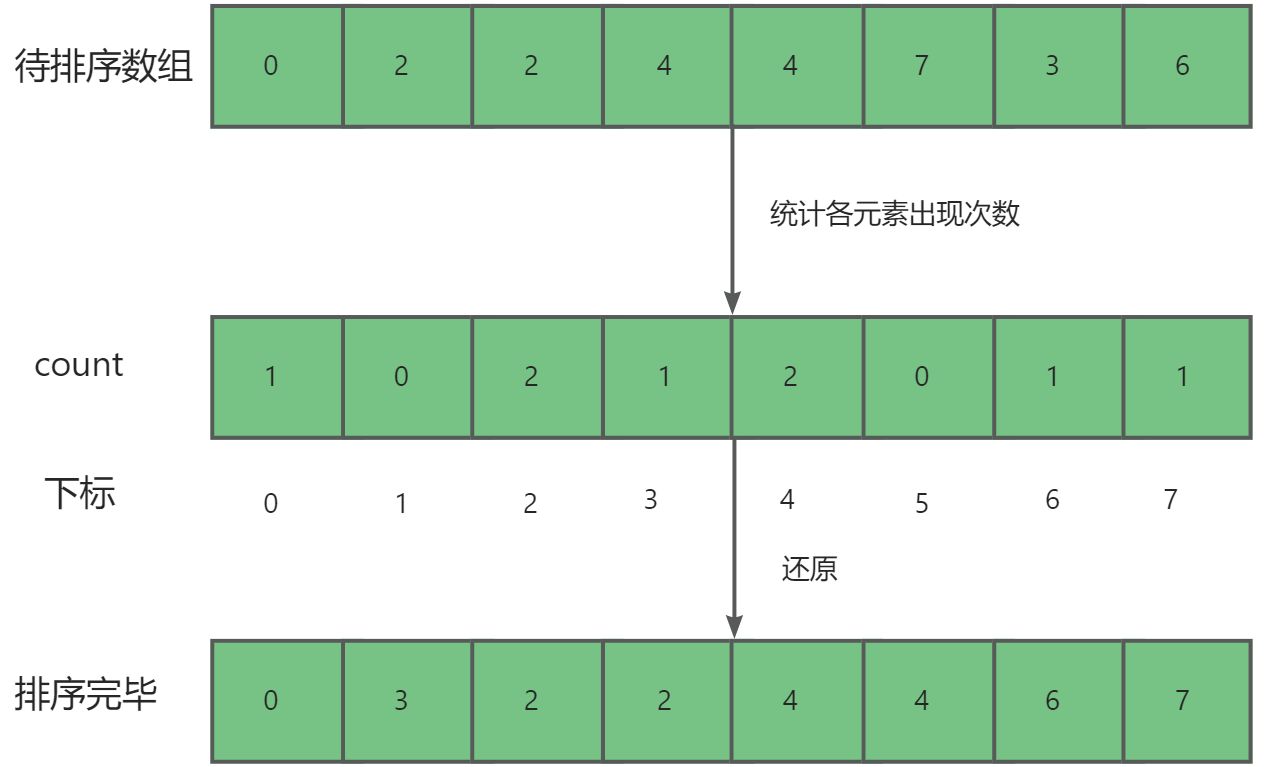
2.3. 动图演示
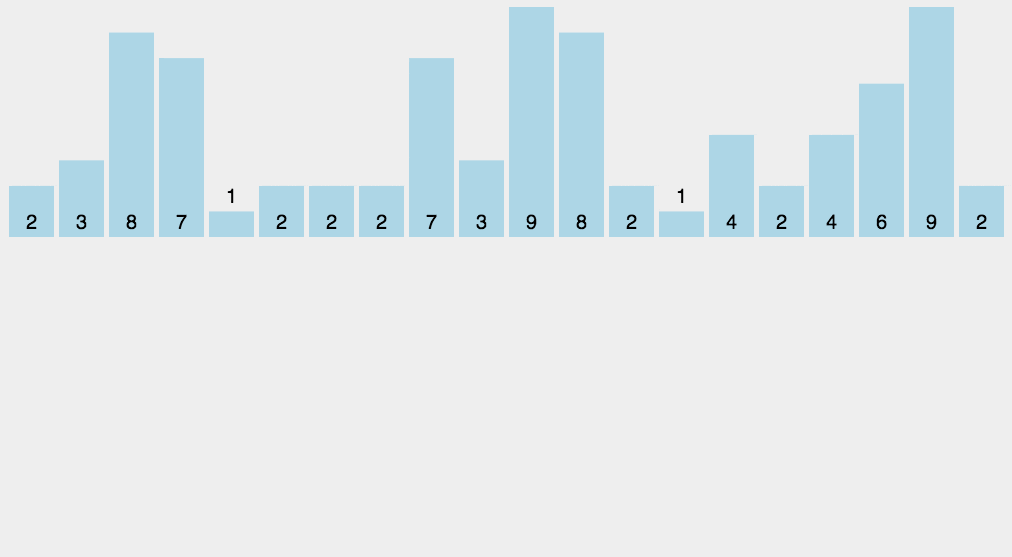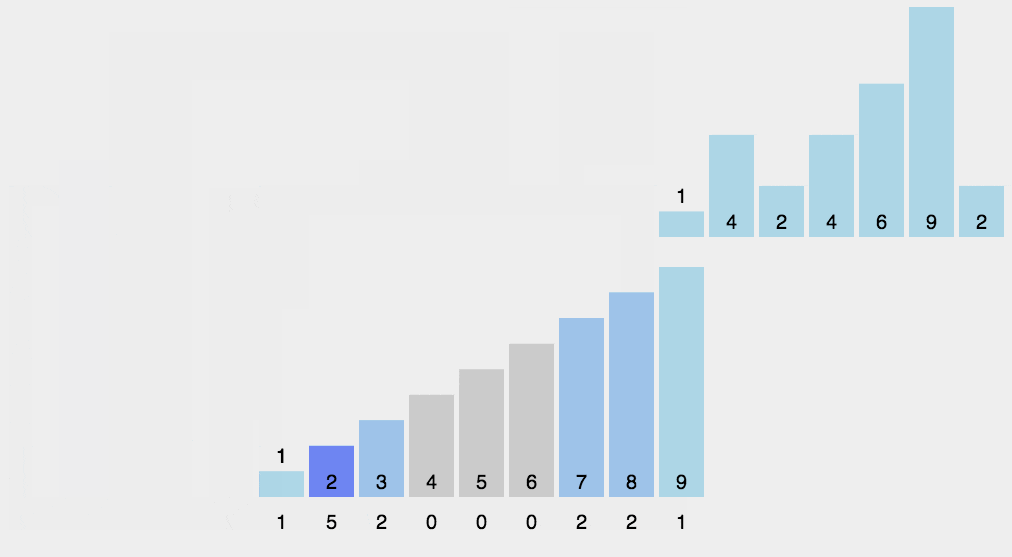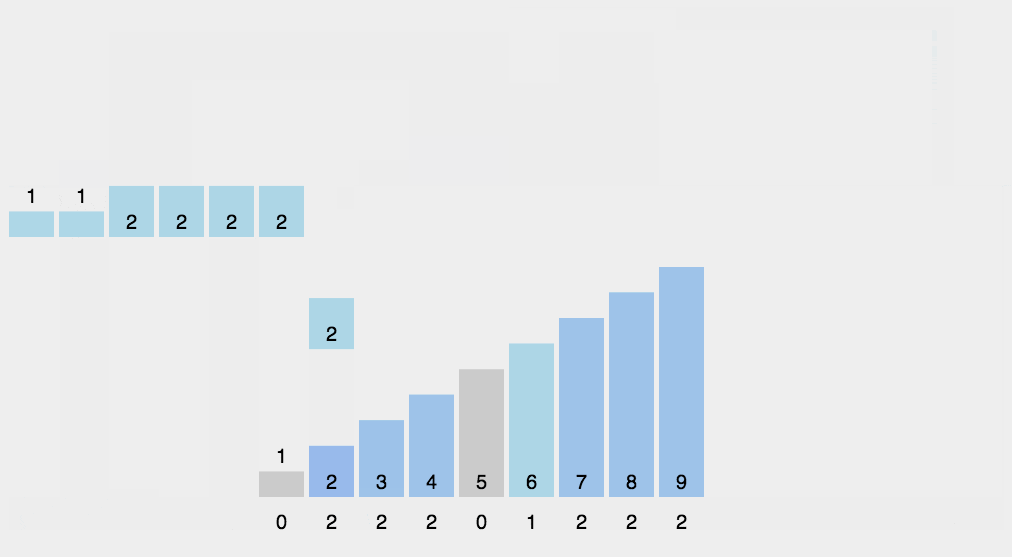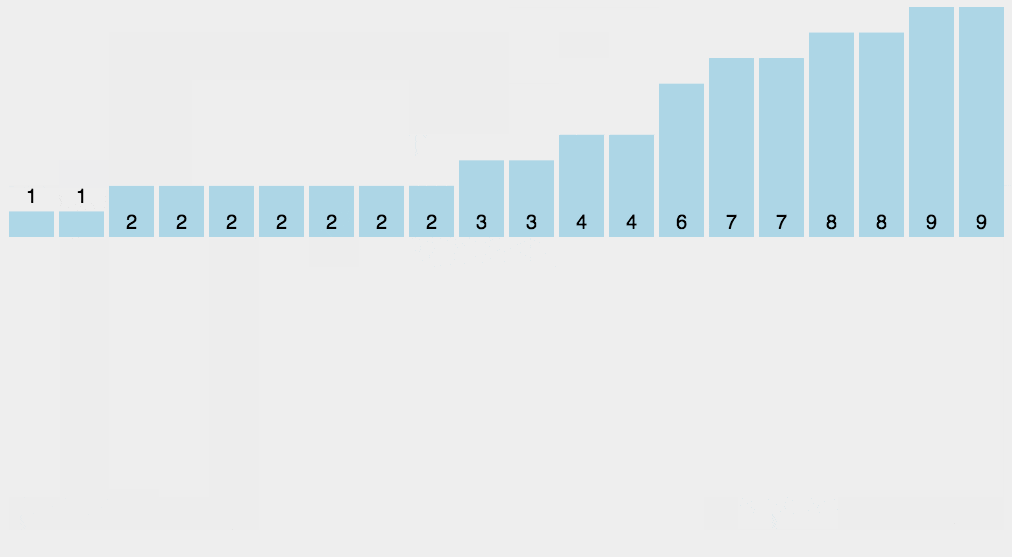
2.4. 代码实现
void CountSort(int* arr, int n)
{
//找出最大与最小元素
int max = arr[0];
int min = arr[0];
for (int i = 0; i < n; i++)
{
if (arr[i] > max)
{
max = arr[i];
}
if (arr[i] < min)
{
min = arr[i];
}
}
int range = max - min + 1;
int* countArray = (int*)malloc(sizeof(int) * range);
if (countArray == NULL)
{
perror("malloc fail:");
return;
}
//初始化
memset(countArray, 0, sizeof(int)*range);
//统计各元素出现次数
for (int i = 0; i < n; i++)
{
countArray[arr[i] - min]++;
}
int j = 0;
for (int i = 0; i < range; i++)
{
while (countArray[i]--)
{
arr[j++] = i + min;
}
}
}
2.5. 复杂度分析
- 时间复杂度:遍历了原数组与range数组,所以时间复杂度为O(N+range)。
- 空间复杂度:开辟了大小为range的数组,所以空间复杂度为O(range)。
3. 桶排序
3.1. 算法思想
桶排序(Bucket Sort) 是一种适用于一定范围内的元素排序的算法。其核心思想是将待排序的元素分配到有限数量的桶中,然后分别对每个桶中的元素进行排序,最后按照顺序将各个桶中的元素依次取出,得到有序序列。
3.2. 算法步骤
- 确定桶的每个桶的元素个数和桶的数量,将待排序数组中的元素分配到对应的桶中。
- 每个桶的元素个数:
bucketsize=(max-min)/n+1,max,min,n分别为数组最大元素,最小元素,以及元素个数。每个桶的范围就是:[min,bucketsize),[min+bucketsize,min+2*bucketsize)…- 桶的数量:
bucketnum=(max-min)/bucketsize+1,bucketsize为每个桶的元素个数。
- 对每个桶中的元素进行排序,可以选择其他排序算法。
- 将各个桶中的元素按照顺序取出,组成最终的有序序列。
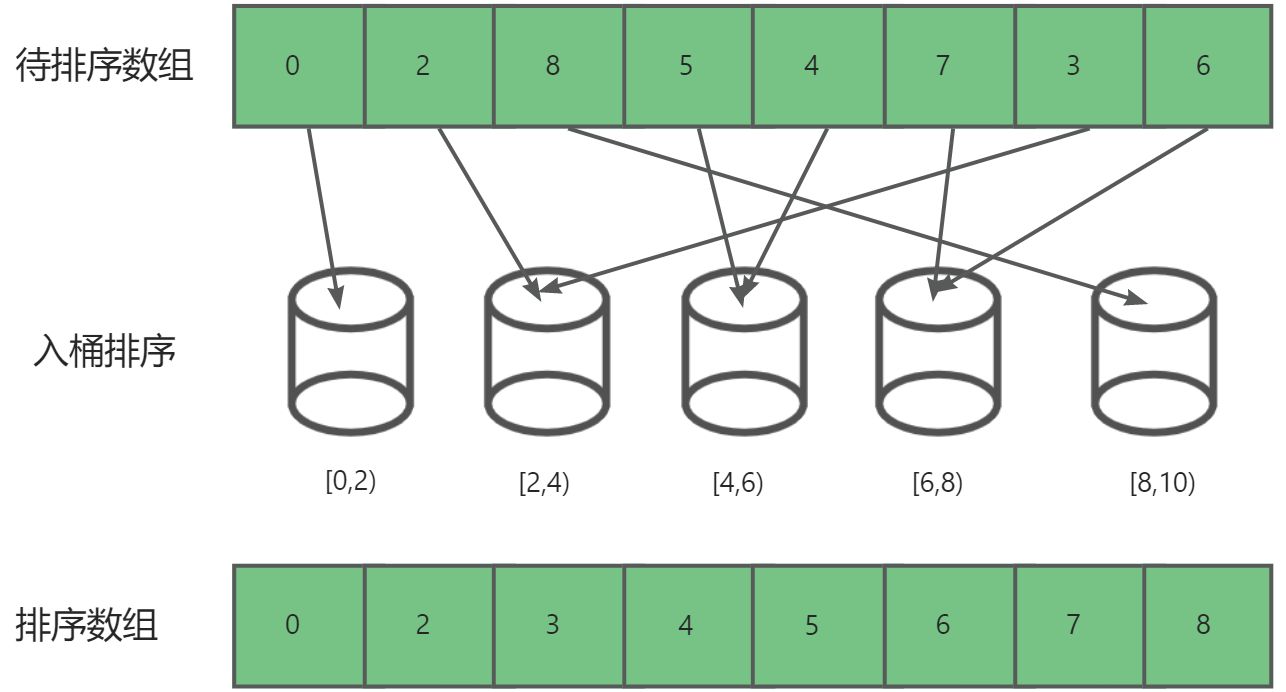
为什么bucketnum与bucketsize 的计算最后要加1?
- 首先是因为除法运算的结果是可以等于0的,而桶的数量与桶最大容纳个数是不可能为0,所以需要加1。
- 其次我们默认每个桶的范围是左闭右开区间,如果不加1最大的元素可能无法进入桶内。
3.3. 动图演示

3.4. 代码实现
void BucketSort(int* arr, int n)
{
//找出最大与最小元素
int max = arr[0];
int min = arr[0];
for (int i = 0; i < n; i++)
{
if (arr[i] > max)
{
max = arr[i];
}
if (arr[i] < min)
{
min = arr[i];
}
}
//每个桶的元素最大个数
int bucketsize = (max - min) / n + 1;
//桶的个数
int bucketnum = (max - min) / bucketsize + 1;
int bucket[bucketnum][bucketsize];
int bucketcount[bucketnum];//每个桶当前元素个数计数器
memset(bucket, 0, sizeof(bucket));
memset(bucketcount, 0, sizeof(bucketcount));
//将元素放入桶中
for (int i = 0; i < n; i++)
{
int index = (arr[i] - min) / bucketsize;//第几个桶
bucket[index][bucketcount[index]] = arr[i];
bucketcount[index]++;//第几个桶的个数++
}
for (int i = 0; i < bucketnum; i++)
{
QuickSort(bucket[i], 0, bucketcount[i] - 1);
}
for (int i = 0; i < bucketnum; i++)
{
int t = 0;
for (int j = 0; j < bucketcount[i]; j++)
{
arr[t++] = bucket[i][j];
}
}
}
3.5. 复杂度分析
- 时间复杂度:假设有N个元素,K个桶。假设元素在各个桶内平均分布,那么每个桶内的元素数量为N/K 。假设排序单个桶使用(N/K)log(N/K)时间,则排序所有桶使用Nlog(N/K)时间。 当桶数量K比较大时,时间复杂度则趋向于O(N) 。合并结果时需要遍历所有桶和元素,时间复杂度为O(N+K)。
- 空间复杂度:需要借助N个元素以及K个桶的辅助空间,所以空间复杂度为O(N+K)。
4. 基数排序
4.1. 算法思想
基数排序(Radix Sort)是一种非比较性的排序算法,适用于对整数或字符串等元素进行排序。其核心思想是将待排序的元素按照位数进行分组,然后依次对每个位数进行稳定的排序,最终得到有序序列。
4.2. 算法步骤
- 确定待排序元素的最大位数,通常通过计算最大元素的位数或者最高位数来确定。
- 从最低位开始,依次对元素按照当前位上的数值进行分组,并且统计每个数组出现次数记录在
counter数组中。(十进制的位范围为 0~9 ,因此需要长度为 10 的统计数组)- 利用前缀和
counter[i] = counter[i - 1] + counter[i]求出每个对应数值的最后一个元素的下标索引。- 倒序遍历,通过每个元素
arr[i]的当前位上的值求出下标索引j=counter[i]-1,并将该元素存入新的数组ret[j]=arr[i]中,最后以ret数组覆盖原数组达到排序该位数的目的。- 重复步骤2,3,4直至达到最大元素的位数,排序完毕。
-
按个位排序
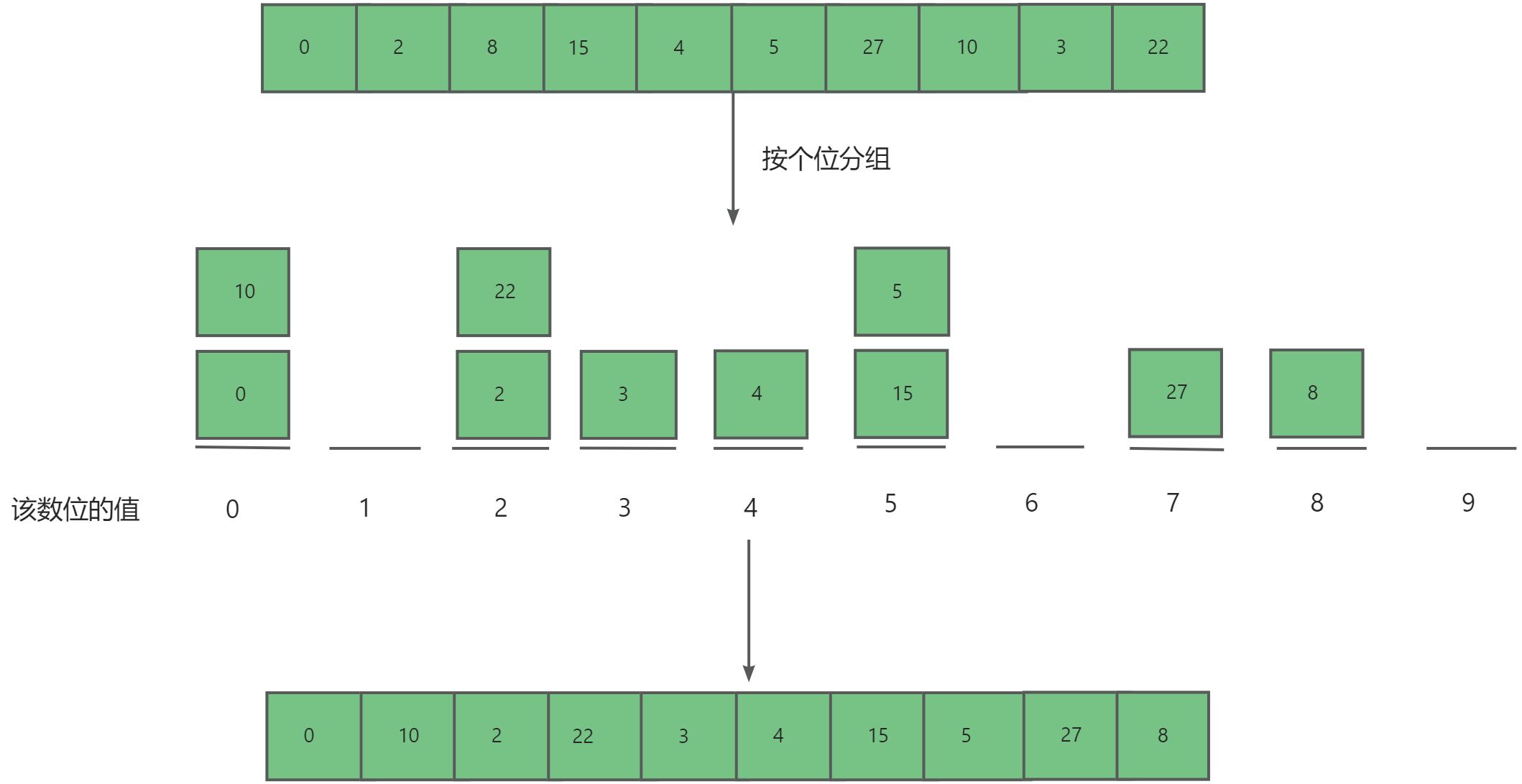
-
按十位排序
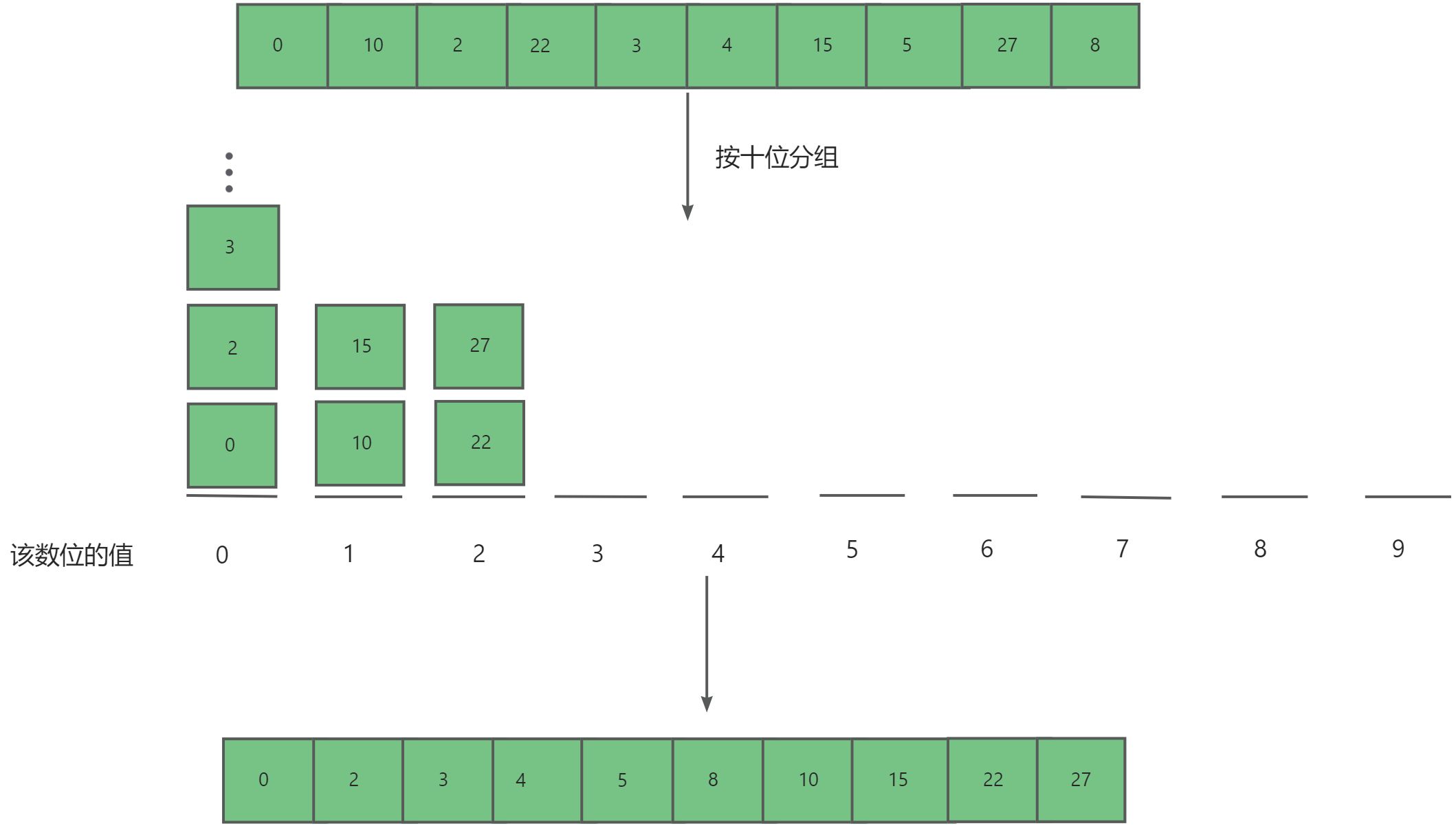
为什么一定要从从最低位开始排序?
在连续的排序轮次中,后一轮排序会覆盖前一轮排序的结果。举例来说,如果第一轮排序结果a<b ,而第二轮排序结果 a>b,那么第二轮的结果将取代第一轮的结果。由于数字的高位优先级高于低位,我们应该先排序低位再排序高位。
4.3. 动图演示

4.4. 代码实现
//获取当前位数的值
int digit(int num, int exp)
{
return (num / exp) % 10;
}
//对当前位数进行排序
void CountSortDigit(int arr[], int n, int exp) {
// 十进制的位范围为 0~9 ,因此需要长度为 10 的统计数组
int* counter = (int*)malloc((sizeof(int) * 10));
if (counter == NULL)
{
perror("malloc fail:");
return;
}
//初始化
memset(counter, 0, sizeof(int)*n);
// 统计 0~9 各数字的出现次数
for (int i = 0; i < n; i++)
{
int d = digit(arr[i], exp);
counter[d]++;
}
// 求前缀和,将“出现个数”转换为“数组索引”
for (int i = 1; i < 10; i++)
{
counter[i] += counter[i - 1];
}
// 倒序遍历,根据统计数组内统计结果,将各元素填入 ret
int* ret = (int)malloc(sizeof(int) * n);
if (ret == NULL)
{
perror("malloc fail:");
return;
}
memset(ret, 0, sizeof(int) * n);
for (int i = n - 1; i >= 0; i--)
{
int d = digit(arr[i], exp);
int j = counter[d] - 1; // 获取 d 在数组中的索引 j
ret[j] = arr[i]; // 将当前元素填入索引 j
counter[d]--;
}
// 覆盖原数组
for (int i = 0; i < n; i++)
{
arr[i] = ret[i];
}
}
void RadixSort(int*arr, int n)
{
// 获取数组的最大元素,用于判断最大位数
int max = arr[0];
for (int i = 0; i < n ; i++)
{
if (arr[i] > max)
{
max = arr[i];
}
}
// 按照从低位到高位的顺序遍历
for (int exp = 1; max >= exp; exp *= 10)
{
CountSortDigit(arr, n, exp);
}
}
4.5. 复杂度分析
- 时间复杂度:设数据量为N、数据为D进制、最大位数为K ,则对某一位执行计数排序使用O(N+D) 时间,排序所有K 位使用O((N + D)K) 时间,时间复杂度为O(N*K)。通常情况下,D和K都相对较小,时间复杂度趋向O(N) 。
- 空间复杂度:基数排序需要借助长度为N和D的统计数组,所以基数排序空间复杂度为O(N+D)。
5. 排序算法的稳定性
5.1. 稳定性的定义
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i] = r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
5.2. 各种排序算法的稳定性
| 排序算法 | 平均时间复杂度 | 最好时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡算法 | O(N2 ) | O(N ) | O(N2 ) | O(1 ) | 稳定 |
| 选择算法 | O(N2 ) | O(N2 ) | O(N2 ) | O(1 ) | 不稳定 |
| 插入排序 | O(N2 ) | O(N ) | O(N2 ) | O(1 ) | 稳定 |
| 希尔排序 | O(N1.3 ) | O(N ) | O(N2 ) | O(1 ) | 不稳定 |
| 快速排序 | O(NlogN) | O(NlogN) | O(N2 ) | O(logN ) | 不稳定 |
| 归并排序 | O(NlogN) | O(NlogN) | O(NlogN) | O(N ) | 稳定 |
| 堆排序 | O(NlogN) | O(NlogN) | O(NlogN) | O(1) | 不稳定 |
| 计数排序 | O(N+K) | O(N+K) | O(N+K) | O(K) | 稳定 |
| 桶排序 | O(N+K) | O(N+K) | O(N2 ) | O(N+K) | 稳定 |
| N) | O(N ) | 稳定 | |||
| 堆排序 | O(NlogN) | O(NlogN) | O(NlogN) | O(1) | 不稳定 |
| 计数排序 | O(N+K) | O(N+K) | O(N+K) | O(K) | 稳定 |
| 桶排序 | O(N+K) | O(N+K) | O(N2 ) | O(N+K) | 稳定 |
| 基数排序 | O(N*K) | O(N*K) | O(N*K) | O(N+K) | 稳定 |








![【YOLOv8改进[CONV]】SPDConv助力YOLOv8目标检测效果 + 含全部代码和详细修改方式 + 手撕结构图](https://img-blog.csdnimg.cn/direct/903b12dde8914e6e968782bc23431980.png)


