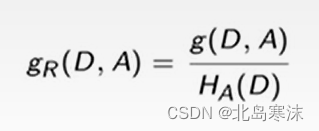首先不考虑算重，因为这题坑点在于当$n\ge 5$时不同结构的树可能生成相同的结果。

那么我们考虑生成不同的系数序列$A$，然后用可重集算一下方案数。考虑将$-1$的边缩去后所形成的树，第$i$层的点表示的是$2^i$，那么如何知道每个节点的正负呢？

由瞪眼大法可知，如果$v$是$u$的儿子，那么$v$会多乘一个系数$2$，说明$v$是中间点，那么假设$u$有$s_u$个儿子，$u$的符号就是$(-1{)}^{s_u}$。同时如果$u$有儿子的话，那么其中$\lceil \frac{s_u}{2}\rceil$个儿子的符号会变成$u$符号的相反数，$\lfloor \frac{s_u}{2}\rfloor$个儿子的符号会和$u$相同。

据此，我们可以自上往下按层数$dp$。比较棘手的问题在于，它与上一层和下一层的状态都有关。这个坑点很隐蔽啊

然后我借鉴题解 设$d{p}_{i,j}$表示$i$个点形成的树，最下面一层有$j$个节点有奇数个儿子节点的方案数。枚举下一层的点数$k$，那么我们知道有$j$个节点符号和父亲不同，剩下的一半相同，一半不同。我们再枚举实际与父亲相同的个数$p$，那么下一层至少需要$|\frac{k-j}{2}-p|$个有奇数个儿子，也就是可以转移到$d{p}_{i+k,|\frac{k-j}{2}-p|}$去。一个错误的想法是，同时转移到$d{p}_{i+k,|\frac{k-j}{2}-p|+2w}$去，但是这样会算重，因为本质上这一层的状态是相同的。不难证明取最小值可以覆盖所有情况。

复杂度$O(n^4)$。

#include<bits/stdc++.h>
#define fi first
#define se second
#define ll long long
#define pb push_back
#define inf 0x3f3f3f3f
using namespace std;
const int mod=1e9+7;
int n;
ll dp[55][55],fac[55],inv[55];
ll fpow(ll x,ll y=mod-2){
	ll z(1);
	for(;y;y>>=1){
		if(y&1)z=z*x%mod;
		x=x*x%mod;
	}return z;
}
void init(int n){
	fac[0]=1;for(int i=1;i<=n;i++)fac[i]=fac[i-1]*i%mod;
	inv[n]=fpow(fac[n]);for(int i=n;i>=1;i--)inv[i-1]=inv[i]*i%mod;
}
void add(ll &x,ll y){
	if((x+=y)>=mod)x-=mod;
}
ll binom(ll x,ll y){
	return fac[x]*inv[y]%mod*inv[x-y]%mod;
}
signed main(){
    cin>>n;init(n);
    dp[1][0]=dp[1][1]=1;
    for(int i=1;i<n;i++){
    	for(int j=0;j<=i;j++){
    		for(int k=max(j,1);k<=n-i;k++){
    			if(k-j&1)continue;
    			for(int p=0;p<=k;p++){
    				add(dp[i+k][abs((k-j)/2-p)],dp[i][j]*inv[p]%mod*inv[k-p]%mod);
				}
			}
		}
	}
	cout<<dp[n][0]*fac[n]%mod;
}