本文主要介绍了一种一种基于神经网络的技术,来解决在含有隐形反馈的基础上进行推荐的关键问题————协同过滤。
2.1 Learning from Implicit Data
y
u
i
=
1
,
(
i
f
i
n
t
e
r
a
c
t
i
o
n
(
u
s
e
r
u
,
i
t
e
m
i
)
i
s
o
b
s
e
r
v
e
d
)
y_{ui} = 1,(if interaction (user u, item i) is observed)
yui=1,(ifinteraction(useru,itemi)isobserved)
y
u
i
=
0
,
o
t
h
e
r
w
i
s
e
y_{ui} = 0,otherwise
yui=0,otherwise
值为1并不代表用户u对i感兴趣,同样,为0也不代表用户u对i不感兴趣,且作为缺失数据处理
2.2 Matrix Factorization
https://blog.csdn.net/SGDBS233/article/details/125838049
内积函数的缺陷

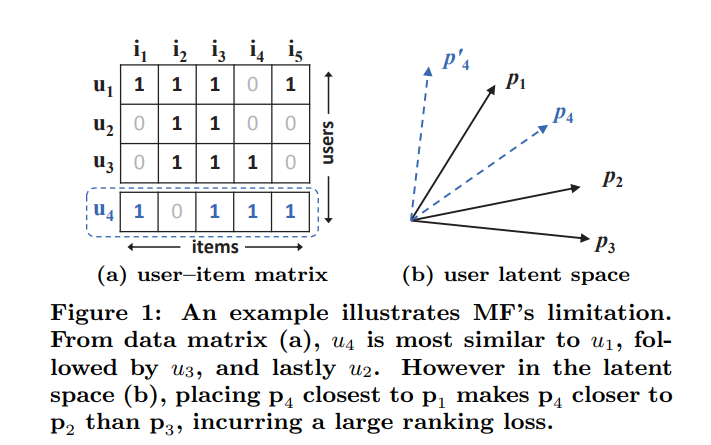
两行数据的相似度相似度可以用向量的内积来计算
我们计算前三行数据,可以得到
s
32
>
s
12
>
s
13
s_{32}>s_{12}>s_{13}
s32>s12>s13,所以可以绘制出如
b
b
b图的形式
但是如果我们计算
s
4
s_4
s4,可得
s
41
>
s
43
>
s
42
s_{41}>s_{43}>s_{42}
s41>s43>s42,会向量
p
4
p_4
p4发现不管怎么放,都无法同时满足这个要求,从而导致误差排名加大。
3. NEURAL COLLABORATIVE FILTERING
3.1 General Framework通用框架
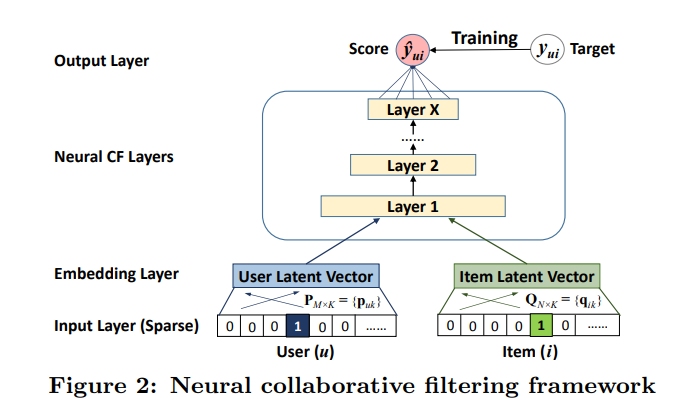
- 将user和item转化为one-hot编码作为Input Layer的输入。
- Embedding Layer是一个全连接层。
- NCF层被称作为神经协作过滤层,它将预测分数。
总体模型如下:
y
^
u
i
=
f
(
P
T
v
u
U
,
Q
T
v
i
I
∣
P
,
Q
,
Θ
f
)
\hat{y}_{ui}=f(P^Tv_u^U,Q^Tv_i^I|P,Q,\Theta_f)
y^ui=f(PTvuU,QTviI∣P,Q,Θf)
其中
P
,
Q
P,Q
P,Q分别表示用户和项目的潜在因素矩阵,
,
Θ
f
,\Theta_f
,Θf表示模型
f
f
f的参数。
3.1.1 NCF的学习 Learning NCF
为了学习模型参数,现有的pointwise方法大多使用了平方损失的回归。
考虑到隐性反馈的一类性质,我们可以将 y u i y_{ui} yui的值作为一个标签,1表示项目i 和用户u相关,否则为0。这样 y ^ u i \hat{y}_{ui} y^ui就是一个概率,所以我们可以用似然函数来定义误差:
p
(
y
,
y
−
∣
P
,
Q
,
Θ
f
)
=
Π
(
u
,
i
)
∈
y
y
^
u
i
Π
(
u
,
i
)
∈
y
−
(
1
−
y
^
u
i
)
\ p(y,y^-|P,Q,\Theta_f)=\mathop{\Pi}\limits_{(u,i)\in y} \hat{y}_{ui}\mathop{\Pi}\limits_{(u,i)\in y^-}(1-\hat{y}_{ui})
p(y,y−∣P,Q,Θf)=(u,i)∈yΠy^ui(u,i)∈y−Π(1−y^ui)
取对数:
L
=
−
∑
(
u
,
i
)
∈
y
∪
y
−
y
u
i
log
y
^
u
i
+
(
1
−
y
u
i
)
log
(
1
−
y
^
u
i
)
L=-\sum\limits_{(u,i)\in y\cup y^-}y_{ui}\log\hat{y}_{ui}+(1-y_{ui})\log(1-\hat{y}_{ui})
L=−(u,i)∈y∪y−∑yuilogy^ui+(1−yui)log(1−y^ui)
这是NCF方法需要去最小化的目标函数,并且可以通过使用随机梯度下降(SGD)来进行训练优化。
3.2 广义矩阵分解 Generalized Matrix Factorization (GMF)
输入层是一个one-hot编码,所以用
P
T
v
u
U
P^Tv_u^U
PTvuU表示用户的潜在向量
p
u
p_u
pu,
Q
T
v
i
I
Q^Tv_i^I
QTviI表示项目潜在向量
q
i
q_i
qi
那么第一层CF层映射函数为
ϕ
(
p
u
,
q
i
)
=
p
u
⊙
q
i
\phi(p_u,q_i)=p_u\odot q_i
ϕ(pu,qi)=pu⊙qi
其中
⊙
\odot
⊙表示向量逐元素累乘。
然后映射到输出层
y
^
u
i
=
a
o
u
t
(
h
T
(
p
u
⊙
q
i
)
)
\hat{y}_{ui}=a_{out}(h^T(p_u\odot q_i))
y^ui=aout(hT(pu⊙qi))
其中
a
o
u
t
a_{out}
aout为激活函数,非线性情况下一般为
σ
(
x
)
=
1
1
+
e
−
x
\sigma(x)=\frac{1}{1+e^{-x}}
σ(x)=1+e−x1,
h
h
h为连接权,通过loss function来学习它。
3.3 多层感知机 Multi-Layer Perceptron (MLP)
简单地对向量的连接不足以说明用户和项目之间的潜在特征,这对协同过滤建模来说是不够的。为了解决这个问题,我们提出在向量连接上增加隐藏层,使用标准的MLP(多层感知机)学习用户和项目潜在特征之间的相互作用。
即假设一共有
L
L
L层
z
1
=
ϕ
1
(
p
u
,
q
i
)
z_1=\phi_1(p_u,q_i)
z1=ϕ1(pu,qi)
ϕ
2
(
z
1
)
=
a
2
(
W
2
T
z
1
+
b
2
)
\phi_2(z1)=a_2(W_2^Tz_1+b_2)
ϕ2(z1)=a2(W2Tz1+b2)
.
.
.
...
...
ϕ
L
(
z
L
−
1
)
=
a
L
(
W
L
T
z
L
−
1
+
b
L
)
\phi_L(z_{L-1})=a_L(W_L^Tz_{L-1}+b_L)
ϕL(zL−1)=aL(WLTzL−1+bL)
y
^
u
i
=
σ
(
h
T
ϕ
L
(
z
L
−
1
)
)
\hat{y}_{ui}=\sigma(h^T\phi_L(z_{L-1}))
y^ui=σ(hTϕL(zL−1))
对于激活函数
a
x
a_x
ax,文章表示使用ReLu效果最好。
结合GMF和MLP Fusion of GMF and MLP
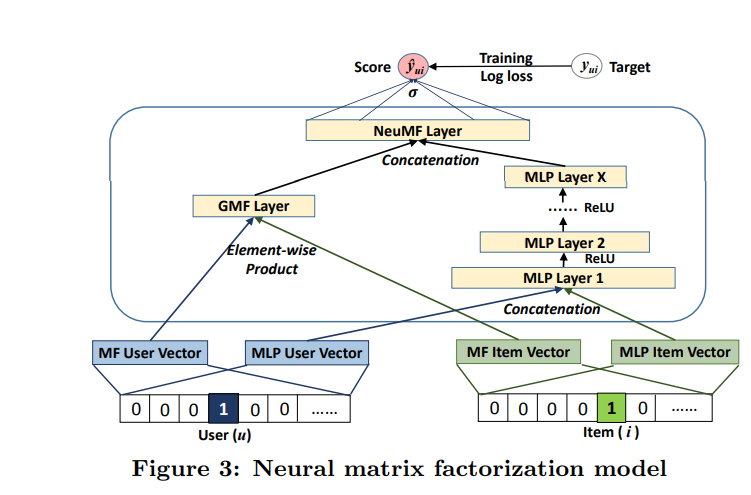
一个直接的解决方法是让GMF和MLP共享相同的嵌入层(Embedding Layer),然后再结合它们分别对相互作用的函数输出,然而,共享GMF和MLP的嵌入层可能会限制融合模型的性能。例如,GMF和MLP必须使用的大小相同的嵌入;对于数据集,两个模型的最佳嵌入尺寸差异很大,使得这种解决方案可能无法获得最佳的组合。
所以我们让GMF和MLP学习独立的嵌入,并结合两种模型通过连接他们最后的隐层输出。
ϕ
G
M
F
=
P
u
G
⊙
q
i
G
\phi^{GMF}=P_u^G\odot q_i^G
ϕGMF=PuG⊙qiG
ϕ
M
L
P
=
σ
(
h
T
ϕ
L
(
z
L
−
1
)
)
\phi^{MLP}=\sigma(h^T\phi_L(z_{L-1}))
ϕMLP=σ(hTϕL(zL−1))
y
^
u
i
=
σ
(
h
T
(
ϕ
G
M
F
⊙
ϕ
M
L
P
)
)
\hat{y}_{ui}=\sigma(h^T(\phi^{GMF}\odot\phi^{MLP}))
y^ui=σ(hT(ϕGMF⊙ϕMLP))
参考文章
https://blog.csdn.net/qq_44015059/article/details/107441512





![[Python]调用pytdx的代码示例](https://img-blog.csdnimg.cn/img_convert/bba4e2d5ac95754514e76cc0e9a8f5ba.png)