目录
- 1.根据二叉树创建字符串
- 2.二叉树的层序遍历
- 3.二叉树的层序遍历II
- 4.二叉树的最近公共祖先
- 5.二叉搜索树与双向链表
- 6.从前序与中序遍历序列构造二叉树
1.根据二叉树创建字符串
根据二叉树创建字符串
给你二叉树的根节点root,请你采用前序遍历的方式,将二叉树转化为一个由括号和整数组成的字符串,返回构造出的字符串。空节点使用一对"()"表示,转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。
解析:
通过题目大家第一反应应该是用递归来处理,是的,通过阅读题目,我们知道有些空串是可以省略的。那省略的规则是什么呢?
1.左右都为空,省略掉
2.左子树不为空,右子树为空,省略掉
3.左子树为空,右子树不为空,不能省略
通过这思路我们可以使用递归去写了,代码如下:
class Solution {
public:
string tree2str(TreeNode* root) {
if(root == nullptr)
{
return string();
}
string str;
str+=to_string(root->val);
//左边不为空或者左边为空,右边不为空,左边括号保留
if(root->left || root->right)
{
str+='(';
str+=tree2str(root->left);
str+=')';
}
//右边不为空,右边括号保留
if(root->right)
{
str+='(';
str+=tree2str(root->right);
str+=')';
}
return str;
}
};
2.二叉树的层序遍历
二叉树的层序遍历
给你二叉树的根节点root,返回其节点值的层序遍历,即逐层的从左到右访问所有节点。
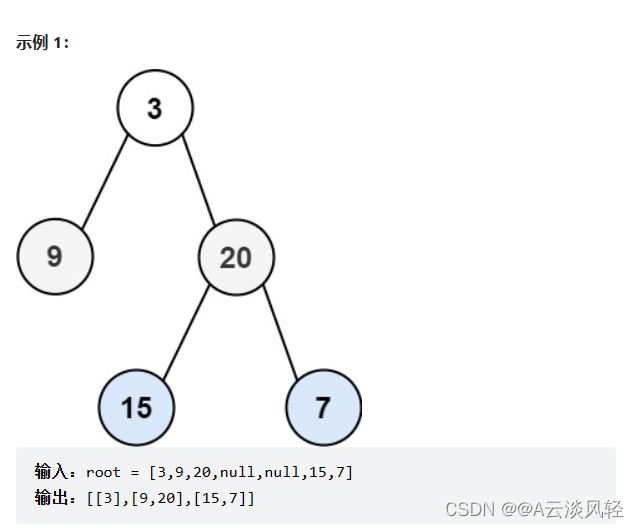
解析:
通过题目意思和输入输出的方式,我们可以使用队列,先入队列的先出队列,当前一层的节点都出队列时,下一层的的节点都进队列,此时下一层的节点个数即是levelSzie = q.size(),通过levelSize控制一层一层出,使用vector对出队列的节点进行保存即可。
代码如下:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> q;
size_t levelSize = 0;
if(root)
{
q.push(root);
levelSize = 1;
}
vector<vector<int>> vv;
while(!q.empty())
{
//控制一层一层出
vector<int> v;
for(size_t i=0;i<levelSize;i++)
{
TreeNode* front = q.front();
q.pop();
v.push_back(front->val);
if(front->left)
{
q.push(front->left);
}
if(front->right)
{
q.push(front->right);
}
}
vv.push_back(v);
//当前层出完了,下一层都进队列,队列的size就是下一层的数据个数
levelSize = q.size();
}
return vv;
}
};
3.二叉树的层序遍历II
二叉树的层序遍历II
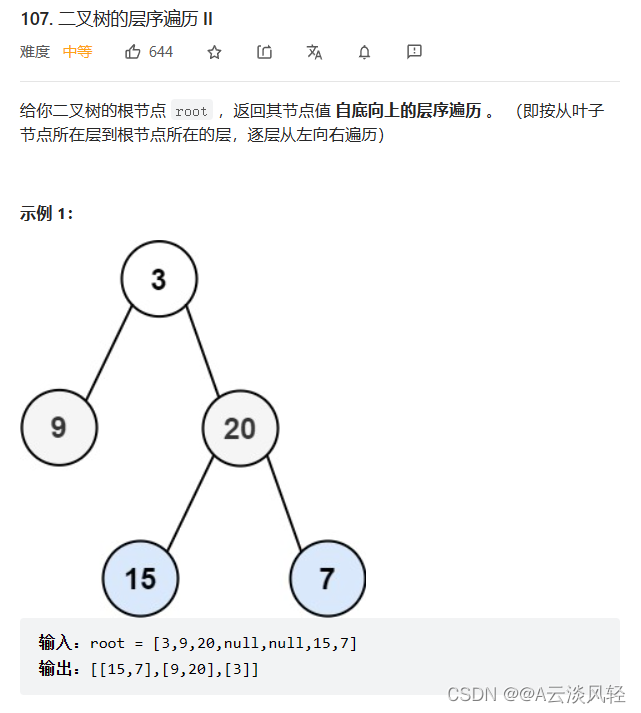
解析:
大家发现这题的结果与上一题有什么区别吗?是不是把上一题的结果逆置一下就行了,没错,还有其他思路,但这个较为简单。
代码如下:
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
queue<TreeNode*> q;
size_t levelSize = 0;
if(root)
{
q.push(root);
levelSize = 1;
}
vector<vector<int>> vv;
while(!q.empty())
{
//控制一层一层出
vector<int> v;
for(size_t i=0;i<levelSize;i++)
{
TreeNode* front = q.front();
q.pop();
v.push_back(front->val);
if(front->left)
{
q.push(front->left);
}
if(front->right)
{
q.push(front->right);
}
}
vv.push_back(v);
//当前层出完了,下一层都进队列,队列的size就是下一层的数据个数
levelSize = q.size();
}
reverse(vv.begin(),vv.end());//逆置
return vv;
}
};
4.二叉树的最近公共祖先
二叉树的最近公共祖先

解析:
思路一:时间复杂度:O(H*N),H是树的高度
这个找公共祖先有什么规则吗?观察下面的图:
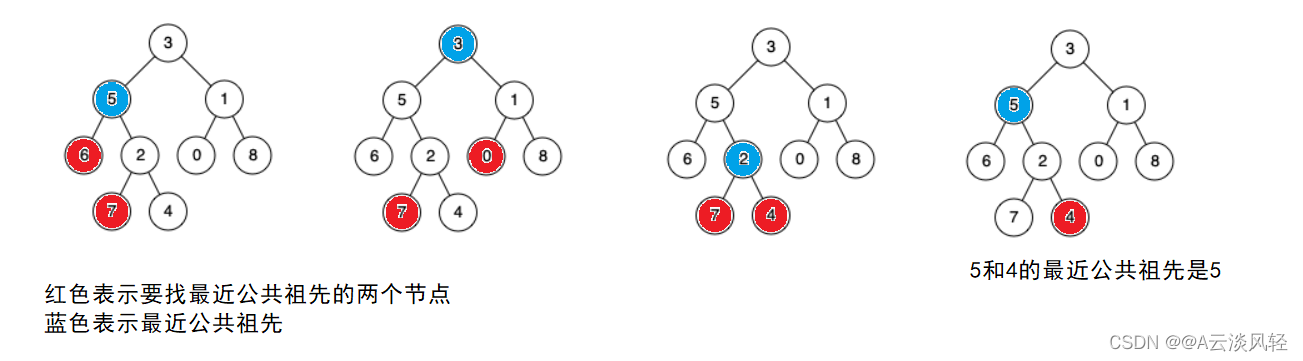
可以知道:一个是它左子树的节点,一个是它右子树的节点,那么它就是最近公共祖先。
代码如下:
class Solution {
public:
bool Find(TreeNode* sub,TreeNode* x)
{
if(sub == nullptr)
{
return false;
}
if(sub == x)
{
return true;
}
return Find(sub->left,x) || Find(sub->right,x);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == nullptr)
{
return nullptr;
}
if(p == root || q == root)
{
return root;
}
//题目给出p、q一定在二叉树中,所以可以这样写
bool pInleft,pInright,qInleft,qInright;
pInleft = Find(root->left,p);
pInright = !pInleft;
qInleft = Find(root->left,q);
qInright = !qInleft;
//如果一个在左子树,一个在右子树,则根节点为结果
//如果都在左,递归到左子树去找
//如果都在右,递归到右子树去找
if((pInleft&&qInright)||(pInright&&qInleft))
{
return root;
}
else if(pInleft&&qInleft)
{
return lowestCommonAncestor(root->left, p,q);
}
else if(pInright&&pInright)
{
return lowestCommonAncestor(root->right, p,q);
}
else
{
//理论上不会走到这
return nullptr;
}
}
};
思路二:上面的时间复杂度为O(H*N),可不可以优化成 O(N)呢?怎么做?
可以使用一个栈,将p,q的路径进行保存,进而转化为链表相交,求交点即可。
代码如下:
class Solution {
public:
bool FindPath(TreeNode* root,TreeNode* x,stack<TreeNode*>& path)
{
if(root == nullptr)
{
return false;
}
path.push(root);
if(root == x)
{
return true;
}
if(FindPath(root->left,x,path))
{
return true;
}
if(FindPath(root->right,x,path))
{
return true;
}
path.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
stack<TreeNode*> pPath,qPath;
FindPath(root,p,pPath);
FindPath(root,q,qPath);
//类似链表相交
while(pPath.size()!=qPath.size())
{
if(pPath.size()>qPath.size())
{
pPath.pop();
}
else
{
qPath.pop();
}
}
while(pPath.top()!=qPath.top())
{
pPath.pop();
qPath.pop();
}
return pPath.top();
}
};
5.二叉搜索树与双向链表
二叉搜索树与双向链表
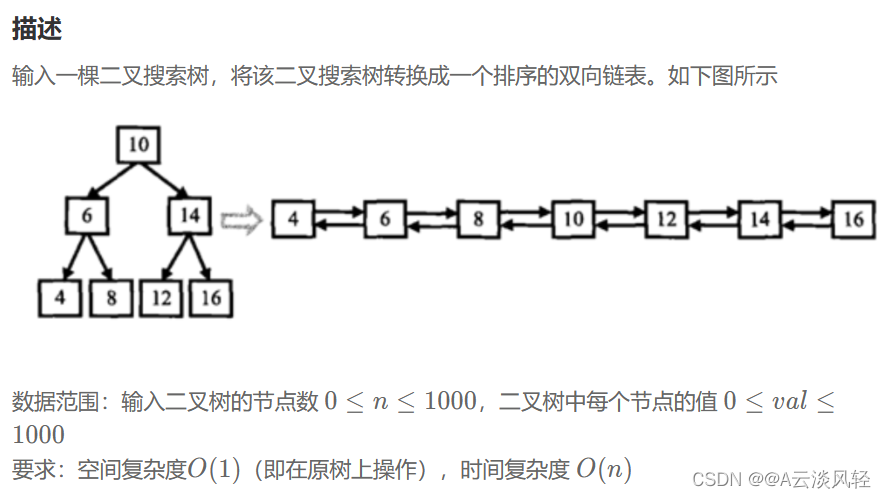
代码如下:
class Solution {
public:
void InOrderConvert(TreeNode* cur,TreeNode*& prev)
{
if(cur == nullptr)
{
return;
}
InOrderConvert(cur->left,prev);
cur->left = prev;
if(prev)
{
prev->right = cur;
}
prev = cur;
InOrderConvert(cur->right,prev);
}
TreeNode* Convert(TreeNode* pRootOfTree) {
if(pRootOfTree == nullptr)
{
return nullptr;
}
TreeNode* prev = nullptr;
InOrderConvert(pRootOfTree,prev);
TreeNode* head = pRootOfTree;
while(head->left)
{
head = head->left;
}
return head;
}
};
6.从前序与中序遍历序列构造二叉树
从前序与中序遍历序列构造二叉树
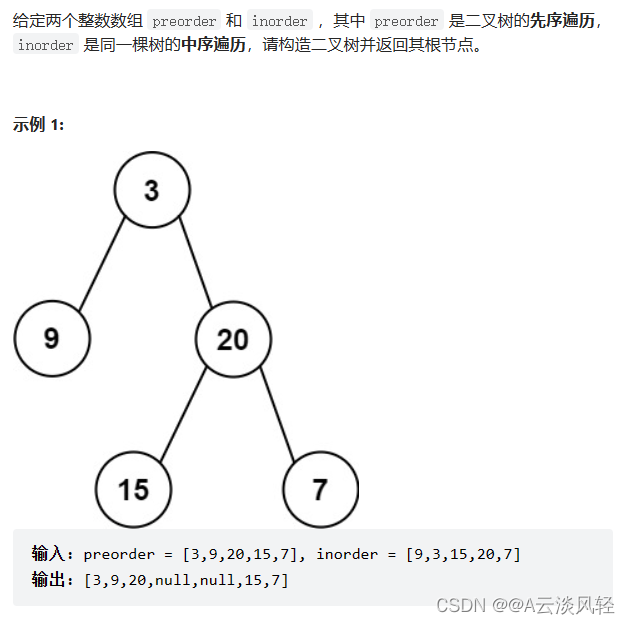
思路:前序可以确定根节点,中序分割左右子树。
代码如下:
class Solution {
public:
TreeNode* _buildTree(vector<int>& preorder,vector<int>& inorder,int& previ,int inbegin,int inend)
{
if(inbegin>inend)
{
return nullptr;
}
TreeNode* root = new TreeNode(preorder[previ++]);
//分割中序
int ini = inbegin;
while(ini<=inend)
{
if(inorder[ini] == root->val)
{
break;
}
else
{
++ini;
}
}
//[inbegin,ini-1] ini [ini+1,inend]
root->left = _buildTree(preorder,inorder,previ,inbegin,ini-1);
root->right = _buildTree(preorder,inorder,previ,ini+1,inend);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int i=0;
return _buildTree(preorder,inorder,i,0,inorder.size()-1);
}
};





![[Python]调用pytdx的代码示例](https://img-blog.csdnimg.cn/img_convert/bba4e2d5ac95754514e76cc0e9a8f5ba.png)