【因果推断python】17

简化形式

手动工具变量

多个工具变量

工具变量的弱点

关键思想

简化形式

不幸的是，我们无法验证第二种IV条件。我们只能支持它。我们可以表达我们的信念，即出生四分之一不会影响潜在的收入。换句话说，人们出生的时间并不表示他们的个人能力或任何其他可能导致收入差异的因素，除了对教育的影响。一个好方法是说，当我们考虑出生季度对收入的影响时，出生季度与随机分配一样好。（它不是随机的。有证据表明，人们倾向于在夏末或某种假期前后怀孕。但我想不出任何充分的理由表明这种模式也会以除教育以外的任何方式影响收入）。

在支持排除限制之后，我们可以继续运行简化形式。简化的形式旨在弄清楚工具变量如何影响结果。从假设出发，因为所有这些影响都是基于对干预的影响，这将为干预如何影响结果提供一些启示。让我们在认真对待回归之前，再一次直观地认识这一点。

plt.figure(figsize=(15,6))
plt.plot(group_data["time_of_birth"], group_data["log_wage"], zorder=-1)
for q in range(1, 5):
    x = group_data.query(f"quarter_of_birth=={q}")["time_of_birth"]
    y = group_data.query(f"quarter_of_birth=={q}")["log_wage"]
    plt.scatter(x, y, marker="s", s=200, c=f"C{q}")
    plt.scatter(x, y, marker=f"${q}$", s=100, c=f"white")

plt.title("Average Weekly Wage by Quarter of Birth (reduced form)")
plt.xlabel("Year of Birth")
plt.ylabel("Log Weekly Earnings");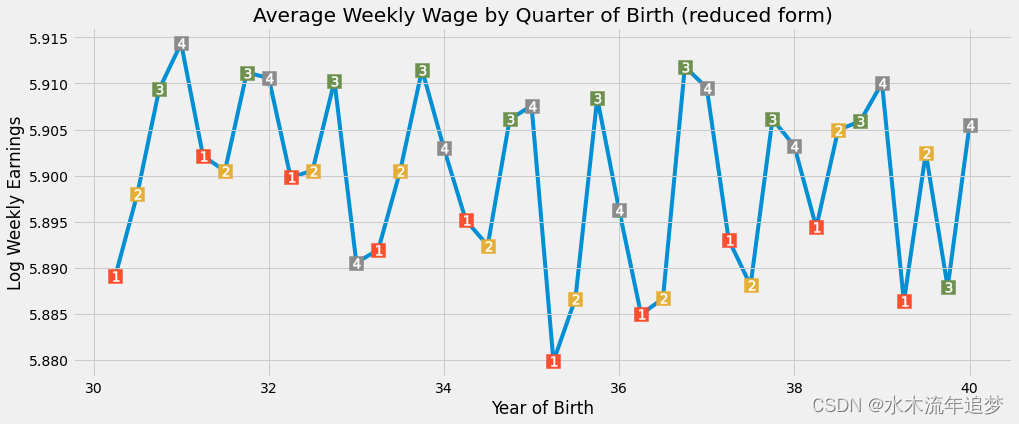

我们再一次可以看到出生季度与收入的季节性关系。当年晚些时候出生的人的收入略高于年初出生的人。为了验证这个假设，我们将再次在对数工资上对工具变量Q4进行回归。我们还将添加与第 1 阶段相同的附加控制变量：

reduced_form = smf.ols("log_wage ~ C(year_of_birth) + C(state_of_birth) + q4", data=factor_data).fit()

print("q4 parameter estimate:, ", reduced_form.params["q4"])
print("q4 p-value:, ", reduced_form.pvalues["q4"])

q4 parameter estimate:,  0.008603484260138683
q4 p-value:,  0.0014949127183684287

我们再次取得了显著的结果。那些出生在每年最后一个季度的人，平均工资高出0.8%。这一次，p值不像以前那样接近于零，但它仍然非常重要，仅为0.0015。

手动工具变量

有了我们的简化形式和第一阶段，我们现在可以通过简化形式来缩放第一阶段的效果。由于第一阶段系数约为0.1，这将使减少的形式系数的影响乘以近10。这将给我们对平均因果效应的无偏见的IV估计： $ATE_{IV}=\frac{\text{Reduced Form}}{1\text{st Stage}}$

reduced_form.params["q4"] / first_stage.params["q4"]

0.08530286492084561

这意味着我们应该期望每增加一年的学费就会增加8%。

获得IV估计值的另一种方法是使用2个阶段最小二乘法2SLS。通过此过程，我们像以前一样执行第一阶段，然后运行第二阶段，其中我们用第一阶段的拟合值替换处理变量

$educ_i=gamma_0+gamma_1*q4_i+gamma_2yob_i+gamma_3sob_i+v_i$ $log\text{(wage)}_i=beta_0+beta_1educ_i+beta_2yob_i+beta_3sob_i+u_i$ $log(wage)_i=beta_0+beta_1[gamma_0+gamma_1*q4_i+gamma_2yob_i+gamma_3sob_i+v_i]+beta_2yob_i+beta_3sob_i+u_i$

需要注意的一点是，我们在执行IV时，我们添加到第二阶段的任何其他控制变量也应添加到第一阶段**。

iv_by_hand = smf.ols("log_wage ~ C(year_of_birth) + C(state_of_birth) + years_of_schooling_fitted",
                     data=factor_data.assign(years_of_schooling_fitted=first_stage.fittedvalues)).fit()

iv_by_hand.params["years_of_schooling_fitted"]

0.08530286492116357

如您所见，参数完全相同。第二种看待IV的方式对于它给出的直觉是有用的。在2SLS中，第一阶段创建一个新版本的干预变量，该版本从省略的变量偏置中清除。然后，我们在线性回归中使用这种清除版本的处理，即第一阶段的拟合值。

然而，在实践中，我们不会手工做IV。不是因为它很麻烦，而是因为我们从第二阶段得到的标准错误有点偏差。相反，我们应该总是让机器为我们完成工作。在Python中，我们可以使用linearmodels软件包以正确的方式运行2SLS。

2SLS的公式有点不同。我们应该在公式中添加第一阶段回归公式 [ ] 之间的部分。在我们的例子中，我们添加了"years_of_schooling~ q4"。不需要将其他控制变量添加到第一阶段，因为如果我们在第二阶段中包含其他控制变量，计算机将自动执行此操作。出于这个原因，我们在第一阶段的公式之外添加了"year_of_birth"和"state_of_birth"。

def parse(model, exog="years_of_schooling"):
    param = model.params[exog]
    se = model.std_errors[exog]
    p_val = model.pvalues[exog]
    print(f"Parameter: {param}")
    print(f"SE: {se}")
    print(f"95 CI: {(-1.96*se,1.96*se) + param}")
    print(f"P-value: {p_val}")
    
formula = 'log_wage ~ 1 + C(year_of_birth) + C(state_of_birth) + [years_of_schooling ~ q4]'
iv2sls = IV2SLS.from_formula(formula, factor_data).fit()
parse(iv2sls)

Parameter: 0.0853028649235057
SE: 0.025540812814298396
95 CI: [0.03524287 0.13536286]
P-value: 0.0008381914659547629

我们可以看到，该参数与我们之前的参数又是完全相同的。额外的好处是，我们现在有有效的标准差。有了这个，我们可以说，我们预计额外1年的教育平均而言将增加8.5%的工资。

多个工具变量

使用计算机的另一个优点是用于运行2SLS估计法，因为它很容易添加多个工具变量。在我们的示例中，我们将使用所有以出生季度标定的虚拟变量作为学校教育年限水平的工具变量。

formula = 'log_wage ~ 1 + C(year_of_birth) + C(state_of_birth) + [years_of_schooling ~ q1+q2+q3]'
iv_many_zs = IV2SLS.from_formula(formula, factor_data).fit()
parse(iv_many_zs)

Parameter: 0.10769370488969798
SE: 0.019557149009493794
95 CI: [0.06936169 0.14602572]
P-value: 3.657974678716869e-08

对于所有3个虚拟变量，估计的教育回报率现在是0.1，这意味着我们应该期望每增加一年的教育收入平均增长10%。让我们将其与传统的 OLS 估计值进行比较。为此，我们可以再次使用2SLS，但现在没有第一阶段。

formula = "log_wage ~ years_of_schooling + C(state_of_birth) + C(year_of_birth) + C(quarter_of_birth)"
ols = IV2SLS.from_formula(formula, data=data).fit()
parse(ols)

Parameter: 0.06732572817657978
SE: 0.00038839984390486563
95 CI: [0.06656446 0.06808699]
P-value: 0.0

据估计，OLS的教育回报率低于2SLS。这表明OVB可能不像我们第一次那么强大。另外，请注意置信区间。2SLS 的 CI 比 OLS 估计值宽得多。让我们进一步探讨一下

工具变量的弱点

在处理IV时，我们需要记住我们是间接估计ATE的。我们的估计取决于第一阶段和第二阶段。如果干预对结果的影响确实很强，那么第二阶段也会很强。但是，如果我们的第一阶段很弱，那么第二阶段有多强并不重要。弱的第一阶段意味着工具变量与干预的相关性非常小。因此，我们无法从工具变量中学到太多有关干预的知识。

IV标准误差的公式有点复杂，不那么直观，所以我们将尝试其他东西来掌握这个问题。我们将模拟数据，其中我们的干预 T 对结果 Y 的影响为2.0，未观察到的混淆变量 U 和额外的对照 X。我们还将在第一阶段模拟具有不同优势的多种工具变量。

$\begin{aligned} &X\sim N(0,2^2) \\ &U\sim N(0,2^2) \\ &T\sim N(1+0.5U,5^2) \\ & Y\sim N(2+X-0.5U+2T\text{,}5^2) \\ &Z\sim N(T,sigma^2)\text{ for }\sigma^2\text{ in }0.1\text{ to }100 \end{aligned}$

np.random.seed(12)
n = 10000
X = np.random.normal(0, 2, n) # observable variable
U = np.random.normal(0, 2, n) # unobservable (omitted) variable
T = np.random.normal(1 + 0.5*U, 5, n) # treatment
Y = np.random.normal(2 + X - 0.5*U + 2*T, 5, n) # outcome

stddevs = np.linspace(0.1, 100, 50)
Zs = {f"Z_{z}": np.random.normal(T, s, n) for z, s in enumerate(stddevs)} # instruments with decreasing Cov(Z, T)

sim_data = pd.DataFrame(dict(U=U, T=T, Y=Y)).assign(**Zs)

sim_data.head()

仔细检查一下，我们可以看到Z和T之间的相关性确实在下降。

corr = (sim_data.corr()["T"]
        [lambda d: d.index.str.startswith("Z")])

corr.head()

Z_0    0.999807
Z_1    0.919713
Z_2    0.773434
Z_3    0.634614
Z_4    0.523719
Name: T, dtype: float64

现在，我们将为每个工具变量运行一个IV模型，并收集ATE估计值和标准误差。

se = []
ate = []
for z in range(len(Zs)):
    formula = f'Y ~ 1 + X + [T ~ Z_{z}]'
    iv = IV2SLS.from_formula(formula, sim_data).fit()
    se.append(iv.std_errors["T"])
    ate.append(iv.params["T"])
plot_data = pd.DataFrame(dict(se=se, ate=ate, corr=corr)).sort_values(by="corr")

plt.scatter(plot_data["corr"], plot_data["se"])
plt.xlabel("Corr(Z, T)")
plt.ylabel("IV Standard Error");
plt.title("Variance of the IV Estimates by 1st Stage Strength");

plt.scatter(plot_data["corr"], plot_data["ate"])
plt.fill_between(plot_data["corr"],
                 plot_data["ate"]+1.96*plot_data["se"],
                 plot_data["ate"]-1.96*plot_data["se"], alpha=.5)
plt.xlabel("Corr(Z, T)")
plt.ylabel("$\hat{ATE}$");
plt.title("IV ATE Estimates by 1st Stage Strength");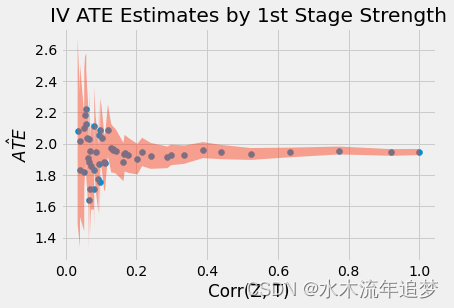

正如我们在上面的图中看到的那样，当 T 和 Z 之间的相关性较弱时，估计值会有很大差异。这是因为当相关性较低时，SE也会增加很多。

另一件需要注意的事情是2SLS是有偏的！即使相关性很高，参数估计值仍未达到 2.0 的真实 ATE。实际上，2.0 甚至不在 95% 的 CI 中！2SLS 仅一致，这意味着如果样本数量足够大，它将接近真实参数值。但是，我们不知道多大才足够大。我们只能坚持一些经验法则来理解这种偏见的行为方式：

2SLS 偏向于 OLS。这意味着，如果 OLS 具有负/正偏差，则 2SLS 也将具有该偏差。2SLS 的优点是，在省略变量的情况下，它至少是一致的，而 OLS 则不是。在上面的例子中，我们未观察到的U对结果产生负面影响，但与干预呈正相关，这将导致负面偏见。这就是为什么我们看到ATE估计值低于真实值（负偏差）。。
偏差将随着我们添加的工具数量而增加。如果我们添加太多的工具，2SLS变得越来越像OLS。

除了知道这种偏差的行为方式之外，最后一条建议是避免在做IV时出现一些常见错误：

手工做IV。正如我们所看到的，即使参数估计是正确的，手动IV也会导致错误的标准误差。SE 不会完全关闭。不过，如果您可以使用软件并获得正确的SE，为什么要这样做呢？
在第一阶段使用OLS以外的任何东西。许多数据科学家遇到IV并认为他们可以做得更好。例如，他们看到一个虚拟的处理，并考虑用逻辑回归替换第一阶段，毕竟，他们正在预测一个虚拟变量，对吧？问题是，这显然是错误的。IV 的一致性依赖于只有 OLS 才能给出的属性，即残差的正交性，因此在第 1 阶段与 OLS 不同的任何内容都会产生偏差。（OBS：有一些现代技术使用机器学习进行IV，但它们的结果充其量是值得怀疑的）。