【C语言之排序】-------六大排序

news2024/11/18 3:29:21

                                                          作者主页：作者主页

                                                          数据结构专栏：数据结构

                                                         创作时间 ：2024年5月18日

前言：

今天我们就给大家带来几种排序的讲解，包括冒泡排序，插入排序，希尔排序，选择排序，堆排序，快速排序等等，在讲解之前我先给大家一个网站，用于查看各种排序的动图，这样有助于我们更加清晰的去了解各种排序：排序动图

冒泡排序：

首先我们来讲解一下冒泡排序，这是我们学习编程第一个接触到的排序，也是较为容易理解的一个排序，下面我们来看一下她是如何实现的。

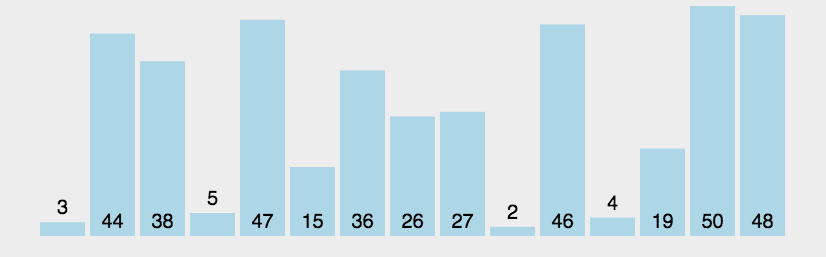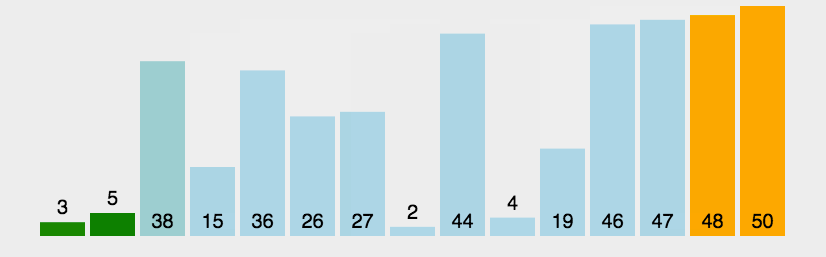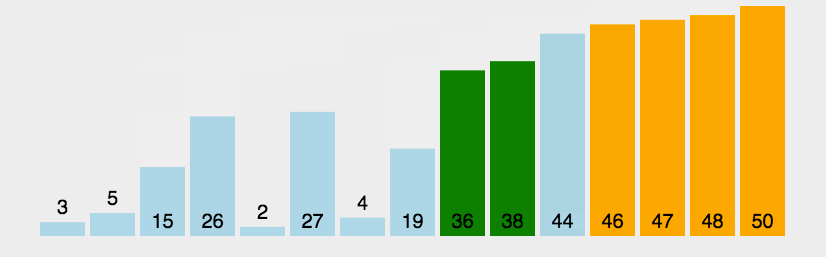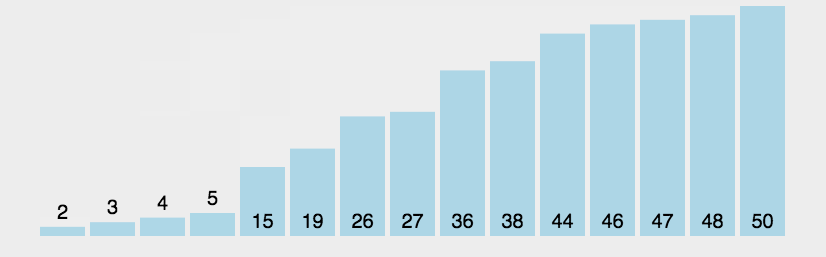
这就是一个大概的冒泡排序的实现过程，其实就是每次都把最大的一个放到最后面，然后下一轮就不需要去管后面最大的那几个。

下面我们来看一下代码应如何实现：

#include<stdio.h>
#include<iostream>
#include<algorithm>
using namespace std;

void print(int* arr, int n) 
{
    for (int i = 0; i < n; i++) 
    {
        printf("%d ", arr[i]);
    }
}

int main() 
{
    int arr[] = { 23,235,13,123523,2342,2342,1,41523,3456,6547,546 };

    int n = sizeof(arr) / sizeof(arr[0]);
    for (int i = 0; i < n - 1; i++)
    {
        for (int j = 0; j < n - 1 - i; j++) 
        {
            if (arr[j] > arr[j + 1]) {  
                swap(arr[j], arr[j + 1]);
            }
        }
    }
    print(arr, n);

    return 0;
}

这就是冒泡排序实现的过程，这里我们就不过多的去说了，还是比较简单的。

时间复杂度：最坏情况：O(N^2)
      最好情况：O(N)
空间复杂度：O(1)

插入排序：

下面我们来看一下插入排序，插入排序的步骤大概是这样的。

1.从第一个元素开始，该元素可以认为已经被排序
2.取下一个元素tem，从已排序的元素序列从后往前扫描
3.如果该元素大于tem，则将该元素移到下一位
4.重复步骤3，直到找到已排序元素中小于等于tem的元素
5.tem插入到该元素的后面，如果已排序所有元素都大于tem，则将tem插入到下标为0的位置
6.重复步骤2~5

图像演示：

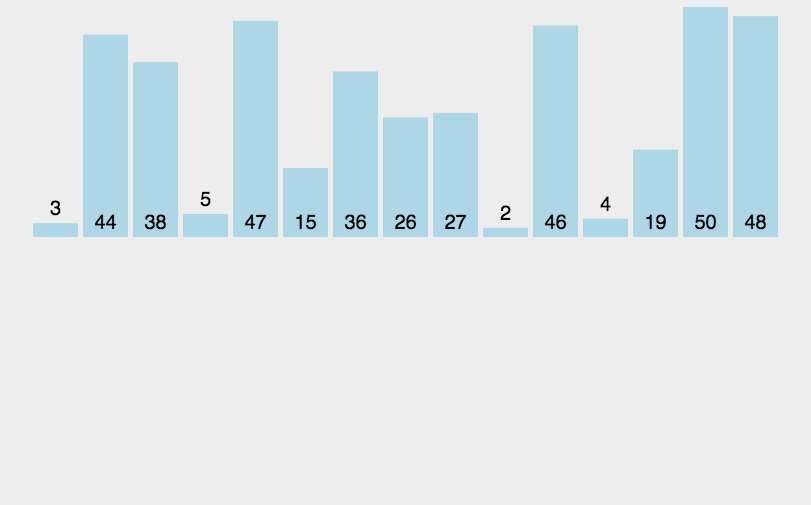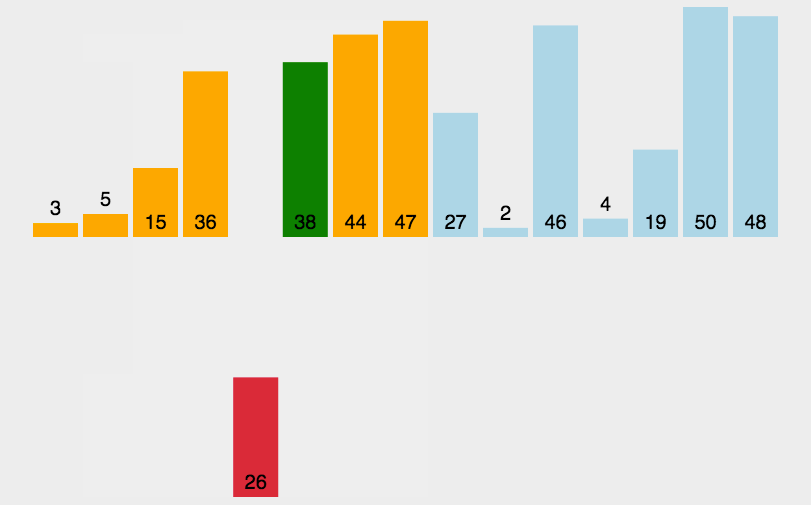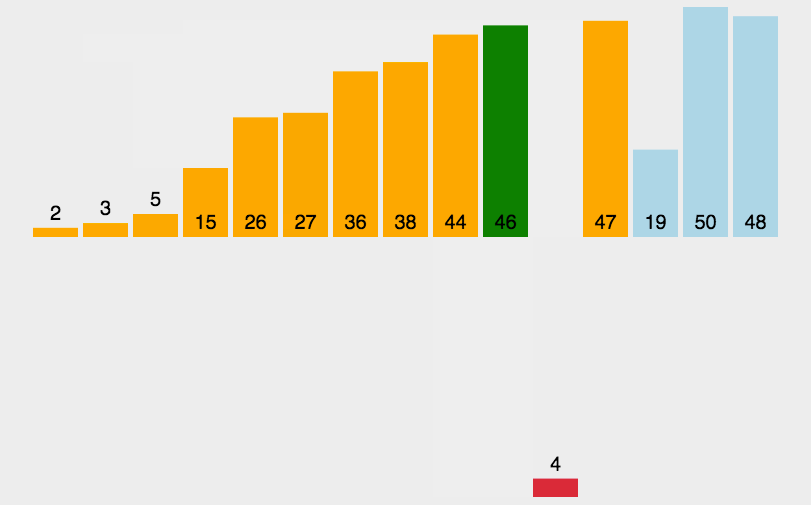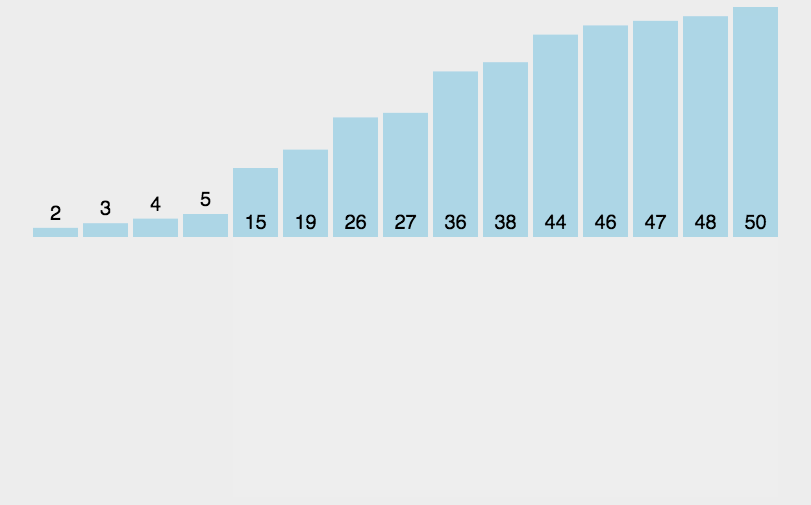
这个图像还是比较清晰易懂的，下面我们来看一下代码吧。

void InsertSort(int* arr, int n)
{
    for (int i = 0; i < n - 1; i++)
    {
        int end = i;
        int temp = arr[end + 1];
        while (end >= 0)
        {
            if (temp < arr[end])
            {
                arr[end + 1] = arr[end];
                end--;
            }
            else
            {
                break;
            }
        }
        arr[end + 1] = temp;
    }
}

插入排序其实就是我们从第一个开始，然后我们用tmp记录要被插入的元素，然后一直和前面的作比较，如果大于前面的，那么就结束，如果小于前面的，我们就令end+1的位置等于end，然后end--就可以了，最后再将temp放到不符合这个条件的位置，就完成了一轮插入排序，后面也是这样循环进行的。

时间复杂度：最坏情况下为O(N*N)，此时待排序列为逆序，或者说接近逆序
      最好情况下为O(N)，此时待排序列为升序，或者说接近升序。
空间复杂度：O(1)

希尔排序：

下面我们来讲一下希尔排序，这个排序其实是比较难懂的，但他的时间复杂度也是较为小的，下面我们看一下如何实现这个排序：

大致步骤：

1.先选定一个小于N的整数gap作为第一增量，然后将所有距离为gap的元素分在同一组，并对每一组的元素进行直接插入排序。然后再取一个比第一增量小的整数作为第二增量，重复上述操作…
2.当增量的大小减到1时，就相当于整个序列被分到一组，进行一次直接插入排序，排序完成。

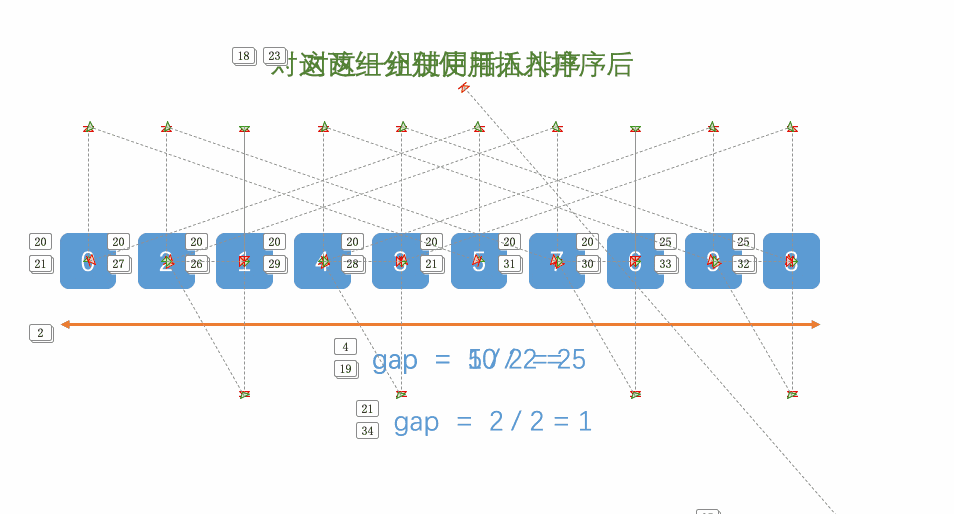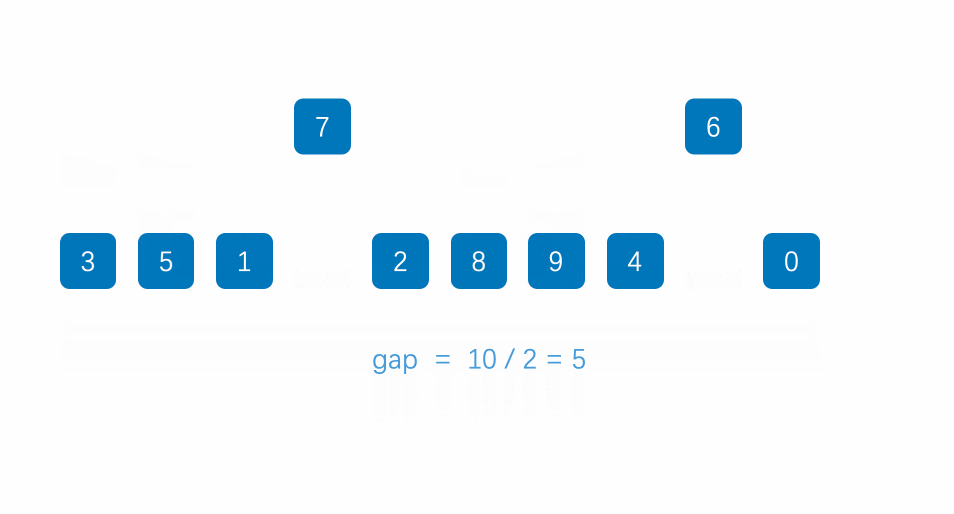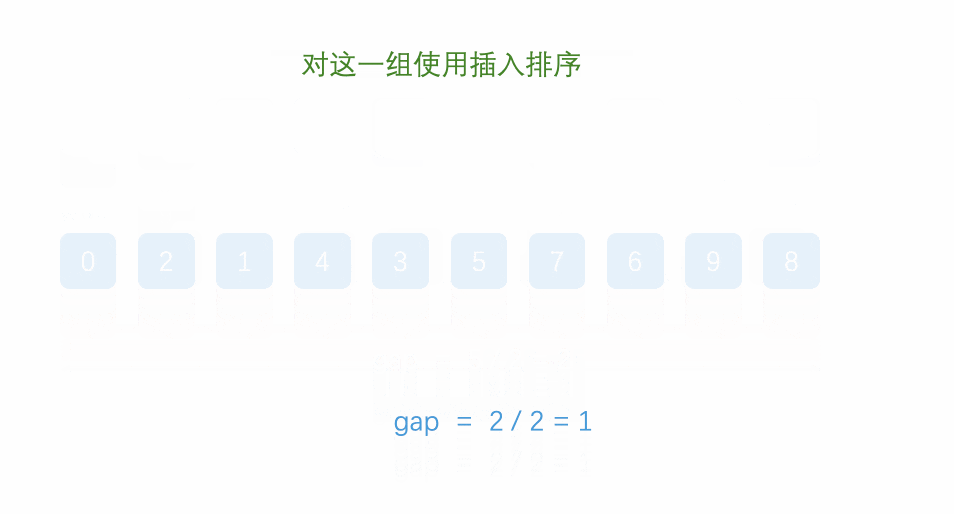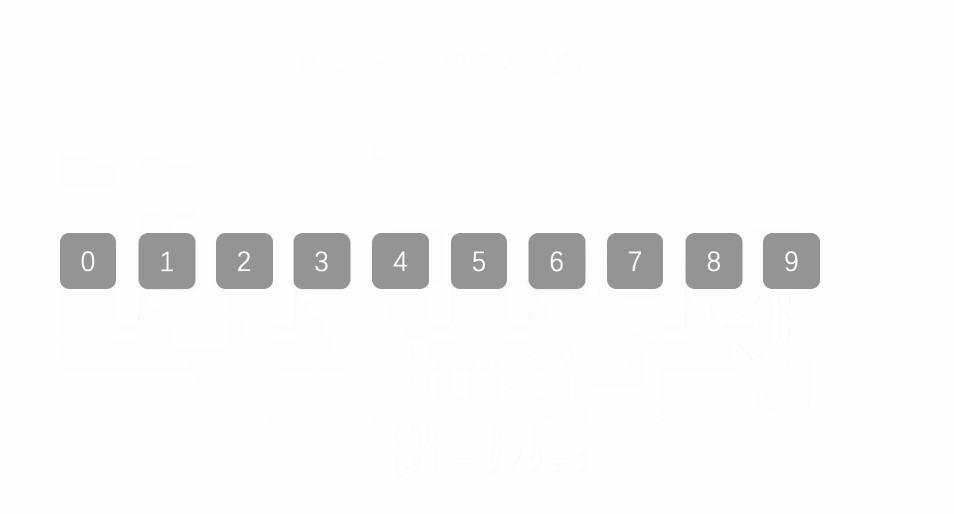
代码：

void ShellSort(int* arr, int n)
{
    int gap = n;
    while (gap > 1)
    {
        gap /= 2;
        for (int i = 0; i < n - gap; i++)
        {
            int end = i;
            int temp = arr[end + gap];
            while (end >= 0)
            {
                if (temp < arr[end])
                {
                    arr[end + gap] = arr[end];
                    end -= gap;
                }
                else
                {
                    break;
                }
            }
            arr[end + gap] = temp;
        }
    }
}

时间复杂度平均：O(N^1.3)
空间复杂度：O(1)

选择排序：

思路：

每次从待排序列中选出一个最小值，然后放在序列的起始位置，直到全部待排数据排完即可。
实际上，我们可以一趟选出两个值，一个最大值一个最小值，然后将其放在序列开头和末尾，这样可以使选择排序的效率快一倍。

下面我们来看一下动图：

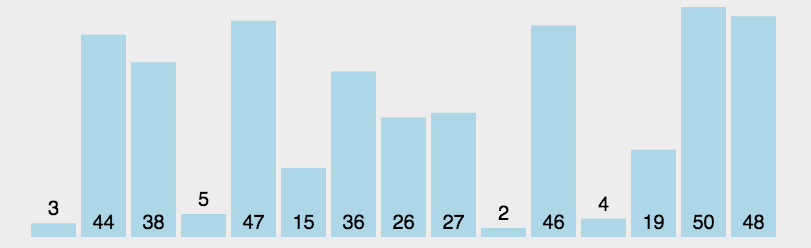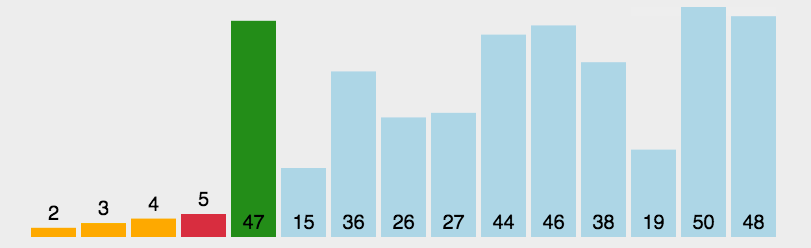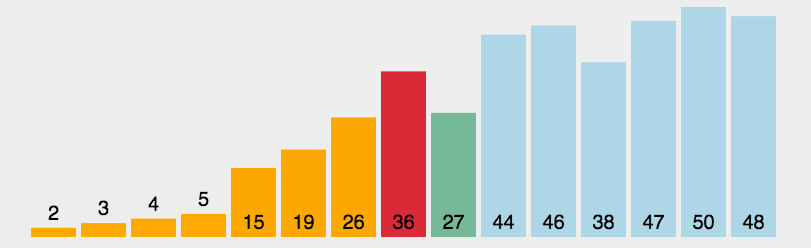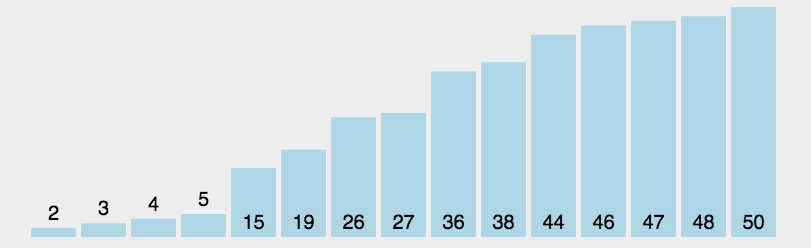
这里我们图片仅供参考，因为我们要用两个下标，一个最大值，一个最小值，以此来提高效率。

void SelectSort(int* arr, int n)
{
    int begin = 0, end = n - 1;
    while (begin < end)
    {
        int max = begin, min = begin;
        for (int i = begin; i <=end; i++)
        {
            if (arr[i] < arr[min])
            {
                min = i;
            }
            if (arr[i] > arr[max])
            {
                max = i;
            }
        }
        swap(arr[begin], arr[min]);
        //为防止最大值在begin位置被换走，我们还要加个判断
        if (begin == max)
        {
            max = min;
        }
        swap(arr[max], arr[end]);
        ++begin;
        --end;
    }
}

 时间复杂度：最坏情况：O(N^2)
      最好情况：O(N^2)
空间复杂度：O(1)

堆排序：

想要更好的了解堆排可以查看这篇博文：堆

在学习堆排之前，首先我们要知道社么是堆，堆其实就是一个二叉树，然后有大根堆和小根堆，然后他们分别长这样：

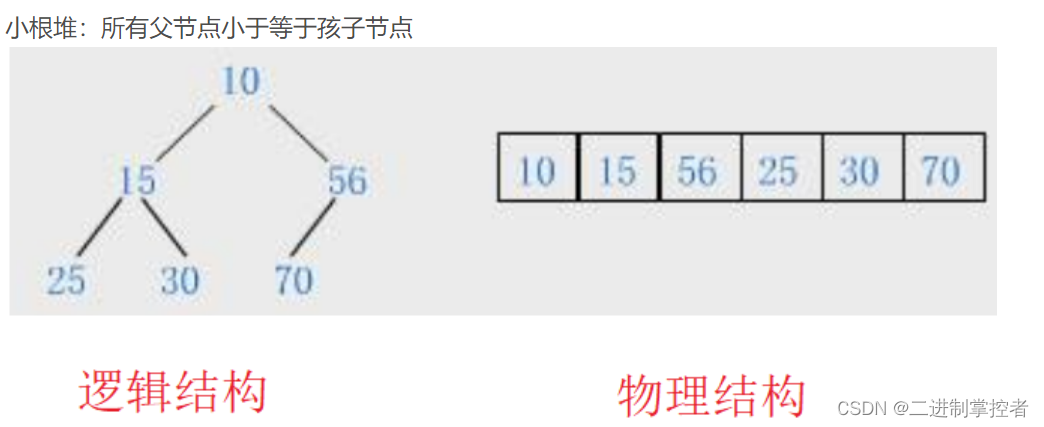
然后我们这里排序的思路就是，比如说大根堆，他的最大值一定在堆顶，然后我们就让他和最后一个数交换，然后不再去管他，再得到一个新的大根堆，继续进行这个操作，这样是不是就实现了呢。

然后这里我们首先还要建堆，然后我们升序的话就建大堆，直接把最大的放在最后一个，然后就不把他看作堆里的数据了。反之，降序就建小堆。下面我们先来看一下如何建堆。

//向上调整(小根堆)
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child>0)
	{
		//if (a[child] < a[parent])//小于就换就相当于建小堆
		if (a[child] > a[parent])//大于就换就会变成大堆
		{
			std::swap(a[child], a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}



//建堆
void HPPush(HP* php, HPDataType x)
{
	assert(php);

	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a,sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc failed!!!");
			return;
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}

	php->a[php->size++] = x;

	//向上调整
	AdjustUp(php->a, php->size - 1);
}

这就是c语言种建堆的一个过程，还是比较麻烦的。

然后有了堆之后，排序就比较简单了。

void HeapSort(int* a, int n)
{
	//首先建堆
	//升序：建大堆
	//降序：建小堆
	/*for (int i=0;i<n;i++)
	{
		AdjustUp(a, i);
	}*/
	//            求最后一个节点的父亲
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}

	int end = n - 1;
	///这里>0即可，因为=0时只剩下最后一个，就不再需要继续进行了
	while (end>0)//思路就是：比如我们升序排序，那么我们就利用大根堆，每次都将最大的那个数放在最顶上，然后将它和最后一个交换，然后让整体的大小--，那么最后一个就不再会受影响
	{
		std::swap(a[0], a[end]);
		AdjustDown(a, end, 0);
		--end;
	}


}

堆排最好的最坏的时间复杂度均为O(n*logn)

空间复杂度为O(1)

快速排序：

快排还是这几个排序种比较麻烦的有一个，但其实也是比较好用的一个

我们这里将会用三种方法来实现这个快速排序：

hoare版本(左右指针法)：

思路：
1、选出一个key，一般是最左边或是最右边的。
2、定义一个begin和一个end，begin从左向右走，end从右向左走。（需要注意的是：若选择最左边的数据作为key，则需要end先走；若选择最右边的数据作为key，则需要bengin先走）。
3、在走的过程中，若end遇到小于key的数，则停下，begin开始走，直到begin遇到一个大于key的数时，将begin和right的内容交换，end再次开始走，如此进行下去，直到begin和end最终相遇，此时将相遇点的内容与key交换即可。（选取最左边的值作为key）
4.此时key的左边都是小于key的数，key的右边都是大于key的数
5.将key的左序列和右序列再次进行这种单趟排序，如此反复操作下去，直到左右序列只有一个数据，或是左右序列不存在时，便停止操作，此时此部分已有序

//快速排序   hoare版本(左右指针法)
void QuickSort(int* arr, int begin, int end)
{
	//只有一个数或区间不存在
	if (begin >= end)
		return;
	int left = begin;
	int right = end;
	//选左边为key
	int keyi = begin;
	while (begin < end)
	{
		//右边选小   等号防止和key值相等    防止顺序begin和end越界
		while (arr[end] >= arr[keyi] && begin < end)
		{
			--end;
		}
		//左边选大
		while (arr[begin] <= arr[keyi] && begin < end)
		{
			++begin;
		}
		//小的换到右边，大的换到左边
		swap(&arr[begin], &arr[end]);
	}
	swap(&arr[keyi], &arr[end]);
	keyi = end;
	//[left,keyi-1]keyi[keyi+1,right]
	QuickSort(arr, left, keyi - 1);
	QuickSort(arr,keyi + 1,right);
}

挖坑法：

递归：

挖坑法思路与hoare版本(左右指针法)思路类似
1.选出一个数据（一般是最左边或是最右边的）存放在key变量中，在该数据位置形成一个坑
2、还是定义一个L和一个R，L从左向右走，R从右向左走。（若在最左边挖坑，则需要R先走；若在最右边挖坑，则需要L先走）

//快速排序法  挖坑法
void QuickSort1(int* arr, int begin, int end)
{
	if (begin >= end)
		return;
	int left = begin,right = end;
	int key = arr[begin];
	while (begin < end)
	{
		//找小
		while (arr[end] >= key && begin < end)
		{
			--end;
		}
		//小的放到左边的坑里
		arr[begin] = arr[end];
		//找大
		while (arr[begin] <= key && begin < end)
		{
			++begin;
		}
		//大的放到右边的坑里
		arr[end] = arr[begin];
	}
	arr[begin] = key;
	int keyi = begin;
	//[left,keyi-1]keyi[keyi+1,right]
	QuickSort1(arr, left, keyi - 1);
	QuickSort1(arr, keyi + 1, right);
}
非递归：
//单趟排
int PartSort(int* arr, int begin, int end)
{
	int key = arr[begin];
	while (begin < end)
	{
		while (key <= arr[end] && begin < end)
		{
			--end;
		}
		arr[begin] = arr[end];
		while (key >= arr[begin] && begin < end)
		{
			++begin;
		}
		arr[end] = arr[begin];
	}
	arr[begin] = key;
	int meeti = begin;
	return meeti;
}

void QuickSortNoR(int* arr, int begin, int end)
{
	stack<int> st;
	//先入右边
	st.push(end);
	//再入左边
	st.push(begin);
	while (!st.empty())
	{
		//左区间
		int left = st.top();
		st.pop();
		//右区间
		int right = st.top();
		st.pop();
		//中间数
		int mid = PartSort(arr, left, right);
		//当左区间>=mid-1则证明左区间已经排好序了
		if (left < mid - 1)
		{
			st.push(mid - 1);
			st.push(left);
		}
		//当mid+1>=右区间则证明右区间已经排好序
		if (right > mid + 1)
		{
			st.push(right);
			st.push(mid + 1);
		}
	}
}

前后指针法：

思路：
1、选出一个key，一般是最左边或是最右边的。
2、起始时，prev指针指向序列开头，cur指针指向prev+1。
3、若cur指向的内容小于key，则prev先向后移动一位，然后交换prev和cur指针指向的内容，然后cur指针++；若cur指向的内容大于key，则cur指针直接++。如此进行下去，直到cur到达end位置，此时将key和++prev指针指向的内容交换即可。

经过一次单趟排序，最终也能使得key左边的数据全部都小于key，key右边的数据全部都大于key。

然后也还是将key的左序列和右序列再次进行这种单趟排序，如此反复操作下去，直到左右序列只有一个数据，或是左右序列不存在时，便停止操作

//快速排序法  前后指针版本
void QuickSort2(int* arr, int begin, int end)
{
	if (begin >= end)
		return;
	int cur = begin, prev = begin - 1;
	int keyi = end;
	while (cur != keyi)
	{
		if (arr[cur] < arr[keyi] && ++prev != cur)
		{
			swap(&arr[cur], &arr[prev]);
		}
		++cur;
	}
	swap(&arr[++prev],&arr[keyi]);
	keyi = prev;
	//[begin,keyi -1]keyi[keyi+1,end]
	QuickSort2(arr, begin, keyi - 1);
	QuickSort2(arr, keyi + 1, end);

}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1792359.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

jmeter的infludb+grafana实时监控平台

jmeter的infludb+grafana实时监控平台

目的&#xff1a;可以实时查看到jmeter拷机信息 框架&#xff1a;将 Jmeter 的数据导入 InfluxDB &#xff0c;再用 Grafana 从 InfluxDB 中获取数据并以特定的模板进行展示 性能监控平台部署实践 一、influxDB 官网&#xff1a;https://www.influxdata.com/downloads/ wget h…
阅读更多...
Unity 自定义房间布局系统 设计与实现一个灵活的房间放置系统 ——物体占用的区域及放置点自动化

Unity 自定义房间布局系统 设计与实现一个灵活的房间放置系统 ——物体占用的区域及放置点自动化

放置物体功能 效果&#xff1a; 功能&#xff1a; 自定义物体占用区域的大小一键调整占用区域调整旋转度数&#xff0c;分四个挡位&#xff1a; NoRotation&#xff1a;该物体不能调整旋转。MaximumAngle&#xff1a;每次转动90。NormalAngle&#xff1a;每次转动45&#xff…
阅读更多...
Vue03-HelloWord

Vue03-HelloWord

一、Hello World 1-1、示例1 1、现有html容器&#xff1b; 2、再有vue实例。 new Vue({});中的{}是配置对象。配置对象是&#xff1a;key&#xff1a;value的格式。 el&#xff1a;element元素。id对应#&#xff0c;class对应. 把容器中变化的数据&#xff0c;交给Vue实例去保…
阅读更多...
嵌入式软件跳槽求指导？

嵌入式软件跳槽求指导？

嵌入式软件行业的跳槽确实需要一些特定的策略和技巧。我这里有一套嵌入式入门教程&#xff0c;不仅包含了详细的视频讲解&#xff0c;项目实战。如果你渴望学习嵌入式&#xff0c;不妨点个关注&#xff0c;给个评论222&#xff0c;私信22&#xff0c;我在后台发给你。 因为这个…
阅读更多...
[Algorithm][动态规划][两个数组的DP][最长公共子序列][不相交的线][不同的子序列][通配符匹配]详细讲解

[Algorithm][动态规划][两个数组的DP][最长公共子序列][不相交的线][不同的子序列][通配符匹配]详细讲解

目录 1.最长公共子序列1.题目链接2.算法原理详解3.代码实现 2.不相交的线1.题目链接2.算法原理详解3.代码实现 3.不同的子序列1.题目链接2.算法原理详解3.代码实现 4.通配符匹配1.题目链接2.算法原理详解3.代码实现 1.最长公共子序列 1.题目链接 最长公共子序列 2.算法原理详…
阅读更多...
Linux网络编程：数据链路层协议

Linux网络编程：数据链路层协议

目录 前言&#xff1a; 1.以太网 1.1.以太网帧格式 1.2.MTU&#xff08;最大传输单元&#xff09; 1.2.1.IP协议和MTU 1.2.2.UDP协议和MTU 1.2.3.TCP协议和MTU 2.ARP协议&#xff08;地址解析协议&#xff09; 2.1.ARP在局域网通信的角色 2.2.ARP报文格式 2.3.ARP报文…
阅读更多...
SpringBoot高手之路02-全局异常处理器

SpringBoot高手之路02-全局异常处理器

RestControllerAdvice 可以将响应数据返回json格式然后响应 那么开始做全局异常处理器 首先先定义一个类 package com.healer.exception;import com.healer.common.Result; import org.springframework.web.bind.annotation.ExceptionHandler; import org.springframework.we…
阅读更多...
AIGC专栏11——EasyAnimateV2结构详解与Lora训练 最大支持768x768 144帧视频生成

AIGC专栏11——EasyAnimateV2结构详解与Lora训练 最大支持768x768 144帧视频生成

AIGC专栏11——EasyAnimateV2结构详解与Lora训练 最大支持768x768 144帧视频生成 学习前言源码下载地址EasyAnimate V2简介技术储备Diffusion Transformer (DiT)Motion ModuleU-VITLora 算法细节算法组成视频VAE视频DIT 数据处理视频分割视频筛选视频描述 模型训练视频VAE视频D…
阅读更多...
Leetcode3168. 候诊室中的最少椅子数

Leetcode3168. 候诊室中的最少椅子数

Every day a Leetcode 题目来源&#xff1a;3168. 候诊室中的最少椅子数 解法1&#xff1a;模拟 代码&#xff1a; /** lc appleetcode.cn id3168 langcpp** [3168] 候诊室中的最少椅子数*/// lc codestart class Solution { public:int minimumChairs(string s){int chair…
阅读更多...
前缀树的实现

前缀树的实现

前缀树的实现 何谓前缀树&#xff1f;实现前缀树节点的选择插入查找查找前缀完整代码 何谓前缀树&#xff1f; 前缀树&#xff08;字典树&#xff09;&#xff0c;使用树状的数据结构存储一个字典的所有单词。前缀树是一个多叉树&#xff0c;一个节点可能有多个子节点&#xf…
阅读更多...
SpringMVC：转发和重定向

SpringMVC：转发和重定向

1. 请求转发和重定向简介 参考该链接第9点 2. forward 返回下一个资源路径&#xff0c;请求转发固定格式&#xff1a;return "forward:资源路径"如 return "forward:/b" 此时为一次请求返回逻辑视图名称 返回逻辑视图不指定方式时都会默认使用请求转发in…
阅读更多...
优化你的WordPress网站：内链建设与Link Whisper Pro插件的利用

优化你的WordPress网站：内链建设与Link Whisper Pro插件的利用

文章目录 内链的重要性WordPress SEO插件&#xff1a;Link Whisper Pro主要功能使用指南下载与安装 结语 在数字营销和网站管理领域&#xff0c;SEO内部优化是提升网站排名、增加流量和提高用户参与度的核心策略。在众多SEO技巧中&#xff0c;内链建设是构建良好网站结构和提升…
阅读更多...
使用Django JWT实现身份验证

使用Django JWT实现身份验证

文章目录 安装依赖配置Django设置创建API生成和验证Token总结与展望 在现代Web应用程序中&#xff0c;安全性和身份验证是至关重要的。JSON Web Token&#xff08;JWT&#xff09;是一种流行的身份验证方法&#xff0c;它允许在客户端和服务器之间安全地传输信息。Django是一个…
阅读更多...
docker实战流程：

docker实战流程：

Docker-compose是docker官方的开源项目&#xff0c;负责实现对docker容器的集群的快速编排&#xff08;通过yaml文件docker-compose.yml管理写好容器之间的调用关系只需一个命令就能实现容器的通识开启或关闭&#xff09;。 类比spring容器&#xff0c;spring管理的是bean而do…
阅读更多...
【乐吾乐3D可视化组态编辑器】3D场景与大屏通信

【乐吾乐3D可视化组态编辑器】3D场景与大屏通信

乐吾乐大屏可视化可以实现大屏页面与内嵌2d/3d场景相互通信&#xff0c;底层原理是利用了iframe通过postMessage发送消息。 3D组态编辑器地址&#xff1a;3D可视化组态 - 乐吾乐Le5le 大屏组态编辑器地址&#xff1a;大屏可视化设计器 - 乐吾乐Le5le 下面以3d场景为例&#…
阅读更多...
C# 判断字符串不等于空的示例

C# 判断字符串不等于空的示例

在C#中&#xff0c;要判断一个字符串是否不等于空&#xff08;即它既不是null也不是空字符串""&#xff09;&#xff0c;方法有如下几种&#xff0c;如下。 方法1 使用逻辑运算符和string.IsNullOrEmpty方法 string myString "123"; // 假设要检查的字…
阅读更多...
Python第二语言（三、Python函数def）

Python第二语言（三、Python函数def）

目录 1. Python函数&#xff08;def 函数名():&#xff09; 1.1 sorted对容器进行排序&#xff1a;无法指定排序规则 1.2 sort对容器自定义排序&#xff1a;可以指定排序规则 1.3 获取变量长度函数&#xff08;len&#xff09; 1.4 函数的定义 1.5 函数-传参定义 1.6 函…
阅读更多...
JFinal学习06 控制器——getPara()接收数据

JFinal学习06 控制器——getPara()接收数据

JFinal学习06 控制器——getPara()接收数据 视频来源https://www.bilibili.com/video/BV1Bt411H7J9/?spm_id_from333.337.search-card.all.click 文章目录 JFinal学习06 控制器——getPara()接收数据零、JFinal数据提交的三种方式一、get提交二、post提交三、url参数化提交四、…
阅读更多...
基于spring boot+vue的校园新闻管理系统

基于spring boot+vue的校园新闻管理系统

随着网络不断的普及发展&#xff0c;校园新闻网站依靠网络技术的支持得到了快速的发展&#xff0c; 首先要从用户的实际需求出发&#xff0c; 通过了解用户的需求开发出具有针对性的首页、校园 新闻、 论坛交流、 留言反馈、 个人中心、 后台管理功能&#xff0c; 利用目前网络…
阅读更多...
MotionEditor_ 通过内容感知扩散编辑视频运动

MotionEditor_ 通过内容感知扩散编辑视频运动

图1. MotionEditor&#xff1a;一种基于扩散的视频编辑方法&#xff0c;旨在将参考视频的运动转移到源视频中。 摘要 现有的基于扩散的视频编辑模型在随时间编辑源视频的属性方面取得了显著进展&#xff0c;但在修改运动信息的同时保持原始主角的外观和背景方面存在困难。为…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023