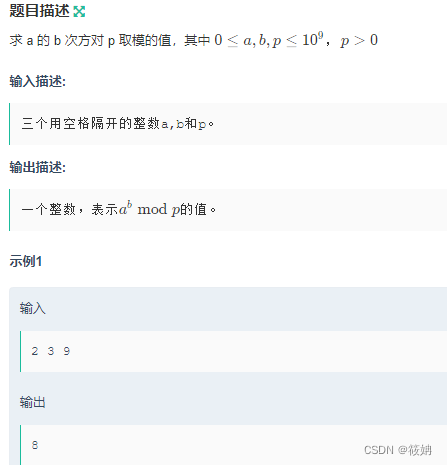
a^b

原题链接：登录—专业IT笔试面试备考平台_牛客网

题目描述

运行代码

#include<iostream>
using namespace std;
long long a,b,c,t=1;
int main()
{
	cin>>a>>b>>c;
	for(;b;b/=2)
	{
		if(b&1)t=t*a%c;
		a=a*a%c;
	}
    cout<<t%c;
}

代码思路：快速幂取模算法

1. 变量定义：首先定义了四个变量，a 代表底数，b 代表指数，c 代表模数，t 初始化为1，用于存储最终结果的中间值。

2. 输入读取：通过 cin>>a>>b>>c; 读取用户输入的底数 a、指数 b 和模数 c。

3. 快速幂循环：通过一个 for 循环处理指数 b 的每一位。循环条件是 b 不为0，每次循环 b 都会右移一位（b/=2），相当于不断地将指数除以2并向下取整。

   • 判断奇偶性并累乘：在循环内部，首先使用条件 if(b&1) 判断 b 当前最低位是否为1，即判断 b 是否为奇数。如果是奇数，则需要将当前的 a 对结果 t 产生的影响累加进去，即执行 t=t*a%c;。这是因为当 b 是奇数时，a^b 实际上是 a 乘以 a 的其他偶数次幂结果，这里是通过累计 t 来逐步构建这个结果。

   • 平方并取模：无论 b 的当前最低位是0还是1，都会执行 a=a*a%c;，这意味着每轮循环都将底数 a 自身平方一次，并对结果取模 c，以控制数值大小，避免溢出。

4. 输出结果：循环结束后，变量 t 存储了 a^b \mod c的计算结果，但为了确保结果的准确性（尽管理论上已经对每步进行了取模，但再次取模作为输出是良好的编程习惯），最终输出时执行 cout<<t%c;。

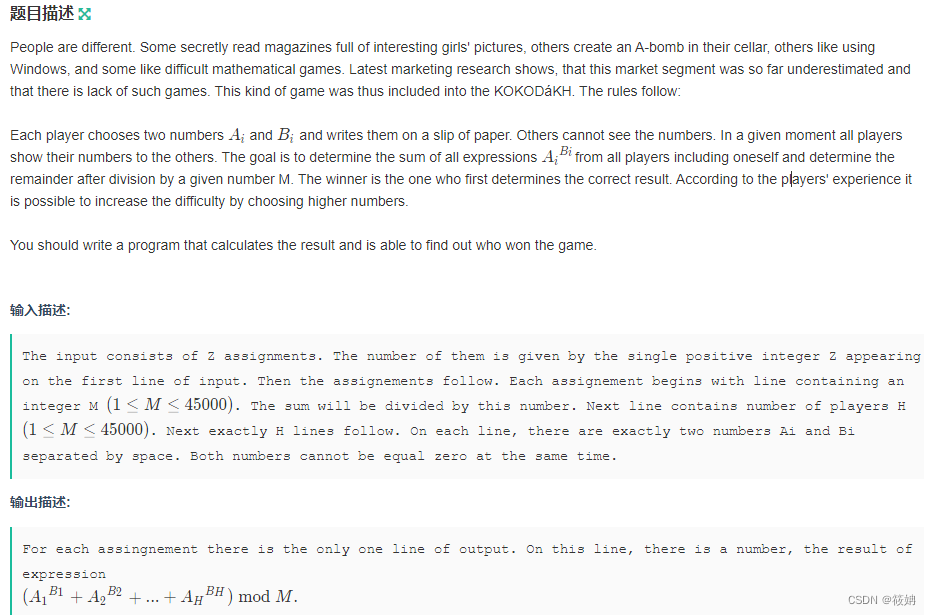
Raising Modulo Numbers

原题链接：登录—专业IT笔试面试备考平台_牛客网

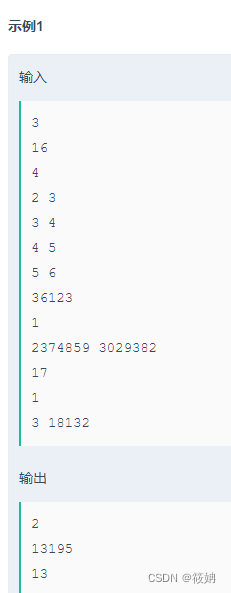
题目描述

 

运行代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll in(){
    ll ans=0,f=1;
    char c=getchar();
    while(c<'0'||c>'9'){
        if(c=='-')f=-1;c=getchar();
    }
    while(c>='0'&&c<='9'){
        ans=ans*10+c-'0';
        c=getchar();
    }
    return ans*f;
}
ll clac(ll a,ll b,ll M){
    ll ans=1;
    for(;b;b>>=1){
        if(b&1)ans=(ll)
            ans*a%M;a=a*a%M;}
    
    return ans;    
}
int main(){
    ll q=in();
    while(q--){
        ll ans=0;
        ll M=in(),n=in();
        for(int i=1;i<=n;i++){
            ll a=in(),b=in();
            ans=(ans+clac(a,b,M))%M;}
        cout<<ans<<endl;
    }
}

代码思路

自定义输入函数in():用于读取一个整数（可以是负数），通过逐字符读取并转换为数字，同时支持负数的输入。它首先初始化结果 ans 为0，符号标志 f 为1（表示正数）。如果读取到的是负号，f 设为-1。随后读取直到遇到非数字字符，再读取数字字符并累积到 ans 中，最后根据 f 返回实际的整数值（正数或负数）。

快速幂取模函数clac():输入参数为底数 a、指数 b 和模数 M。通过循环，每次将指数 b 右移一位（除以2），并根据 b 当前最低位是否为1（即 b 奇偶性）决定是否将 a 乘入结果 ans 中，并始终对 ans 和 a 进行模 M 的运算，以避免数值过大。最后返回计算得到的 a^b%M。

主函数main():首先读取测试用例的数量 q，然后对于每个测试用例，读取模数 M 和需要执行幂运算的次数 n。接下来，进行 n 次循环，每次循环中读取底数 a 和指数 b，调用 clac() 函数计算 a^b \mod MabmodM 的结果，并将每次的结果累加到 ans 中，每次累加后都对 M 取模以确保结果正确。最后，输出所有累加结果对 M 取模后的值。

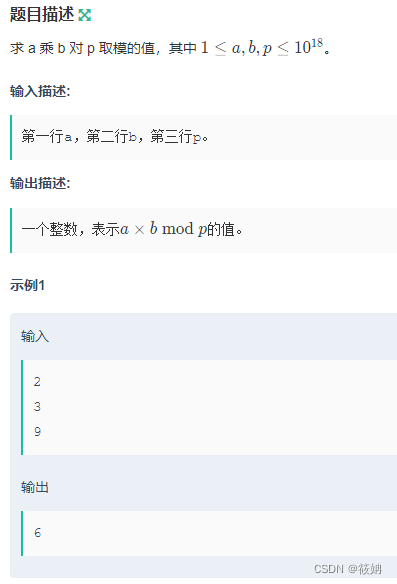
64位整数除法

原题链接:登录—专业IT笔试面试备考平台_牛客网

题目描述

运行代码

#include <iostream>
using namespace std;
int main ()
{
    long long a,b,p,ans = 0;
    cin>>a>>b>>p;
    for (;b;b>>=1,a<<=1,a%=p)
        if (b&1)
            ans = (ans + a) % p;
    cout<<ans%p;
    return 0;
}

代码思路

这段C++代码是一个实现快速幂取模算法的程序，用于计算 a^b%p的值。快速幂算法是一种高效计算大整数幂取模的算法，特别适用于在计算机程序中处理大指数或大模数的情况,能够处理大整数情况，避免了直接计算的大规模乘法和溢出问题。

1. long long a, b, p, ans = 0;：定义四个变量，a 和 b 分别表示底数和指数，p 表示模数，ans 初始化为0，用来存储最终的结果。cin >> a >> b >> p;：从标准输入读取三个数，分别赋值给变量a、b和p。
2. for (;b;b>>=1,a<<=1,a%=p)：这是一个循环结构，循环条件是b非零。在每次循环迭代开始时，将b右移一位（等价于除以2并向下取整），同时将a左移一位（等价于乘以2），并且对a取模p，确保a的值不会过大而导致溢出。
3. if (b&1)：判断b当前最低位是否为1（即判断b是否为奇数），这是快速幂算法的关键，仅当b为奇数时才直接累加a到结果中。
4. ans = (ans + a) % p;：如果b是奇数，则将当前的a加上之前的累加结果ans，并对结果取模p，更新ans的值。
5. cout << ans%p;：循环结束后，输出最终计算结果ans对模数p取模的结果。
6. return 0;：主函数返回0，表示程序正常结束。

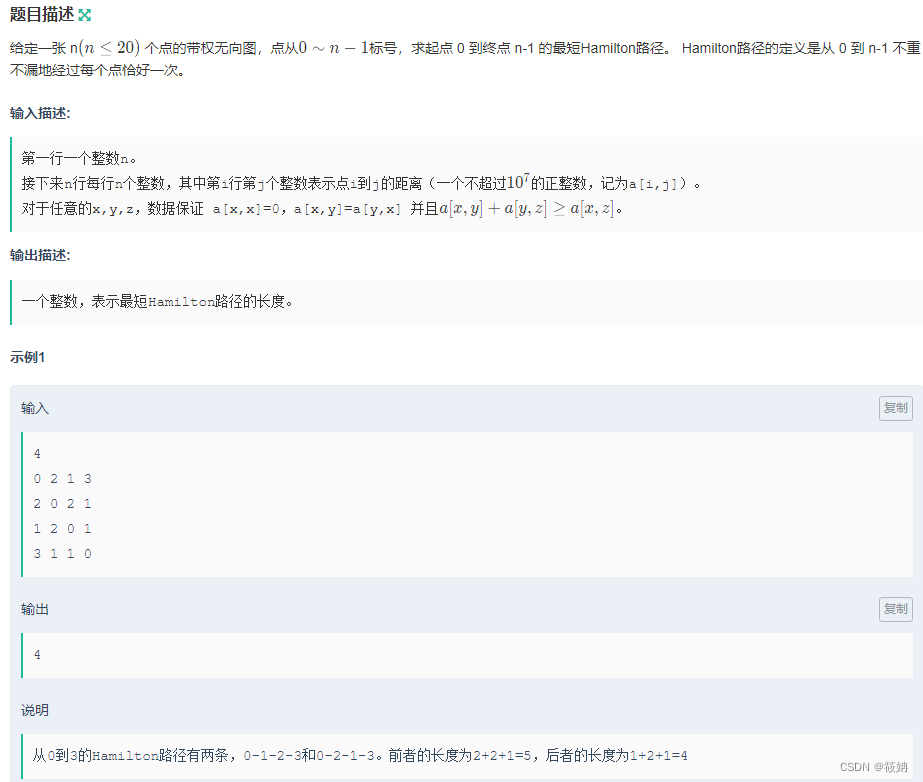
最短Hamilton路径

原题链接：登录—专业IT笔试面试备考平台_牛客网

题目描述

运行代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 20, M = 1 << N;
int n;
int g[N][N];
int dp[M][N];
int main() {
    cin >> n;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            cin >> g[i][j];
    memset(dp, 0x3f, sizeof(dp));
    dp[1][0] = 0;
    for (int s = 1; s < (1 << n); s++) {
        for (int i = 0; i < n; i++) {
            if ((s & (1 << i)) == 0) continue;
            for (int j = 0; j < n; j++) {
                if (i == j) continue;
                if ((s & (1 << j)) == 0) continue;
                dp[s][i] = min(dp[s][i], dp[s ^ (1 << i)][j] + g[j][i]);
            }
        }
    }
    cout << dp[(1 << n) - 1][n - 1] << endl;
    return 0;
}

代码思路

1. 定义常量和变量：N 表示顶点数的上限，M 是状态数（所有顶点的选与不选的组合情况）。g[N][N] 存储图的边权。dp[M][N] 用于动态规划存储中间状态和结果。

2. 输入图的信息。

3. 初始化 dp 数组：将所有值初始化为较大值，除了初始状态 dp[1][0] 设置为 0。

4. 动态规划过程：遍历所有可能的状态 s。对于每个状态和当前顶点 i，通过遍历其他顶点 j 来更新 dp[s][i]，即考虑从之前某个状态去掉当前顶点 i 且到达顶点 j 的最短路径加上从 j 到 i 的边权，取最小值进行更新。

5. 最后输出到达最终状态（所有顶点都选）且在终点 n-1 的最短路径长度，即 dp[(1 << n) - 1][n - 1]。