接口实现

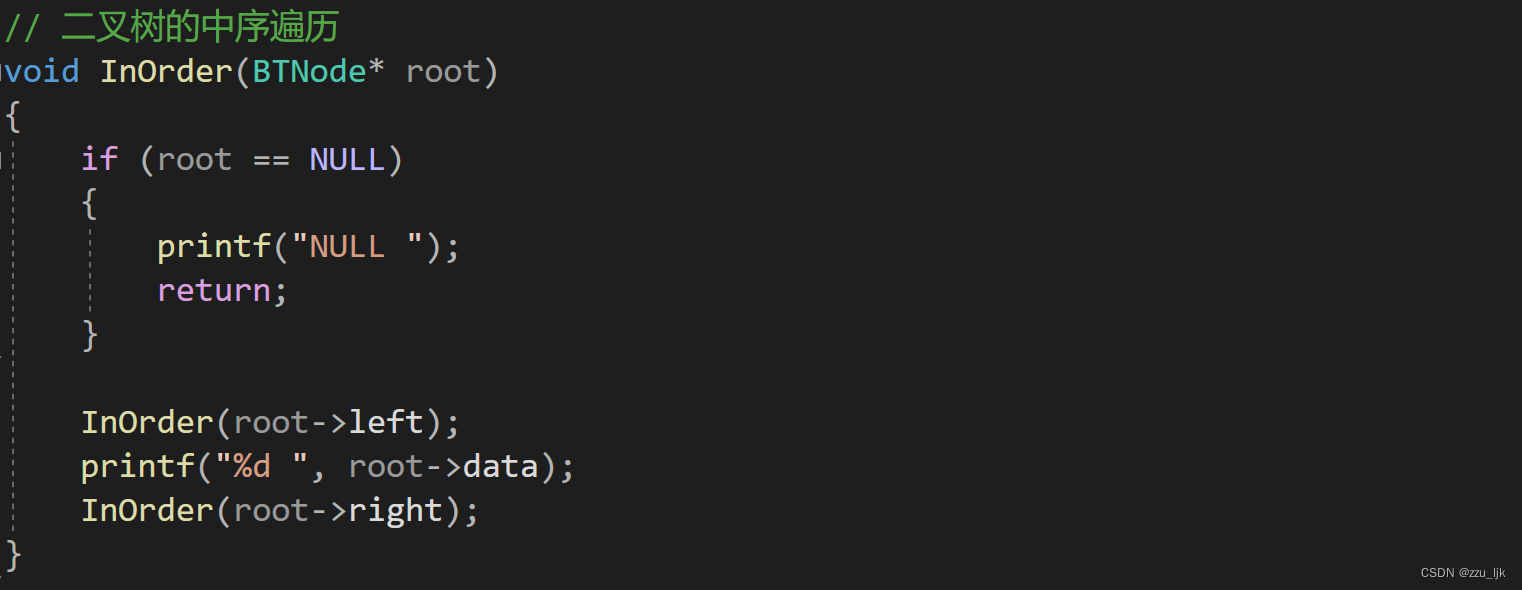
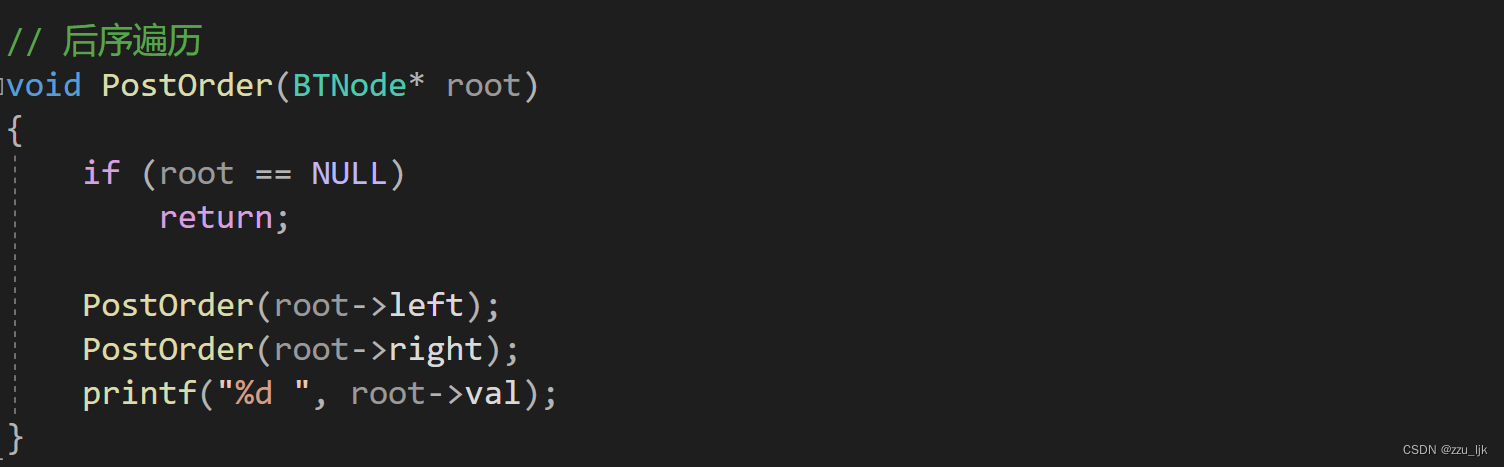
三种基本遍历方式

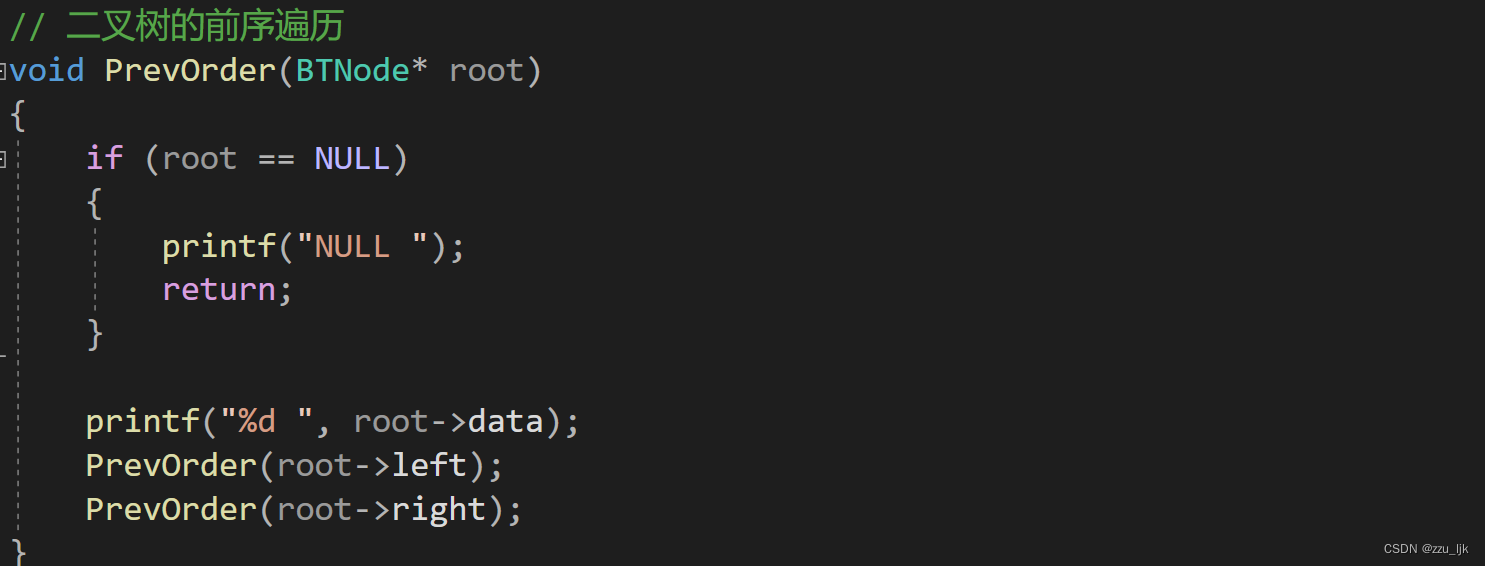
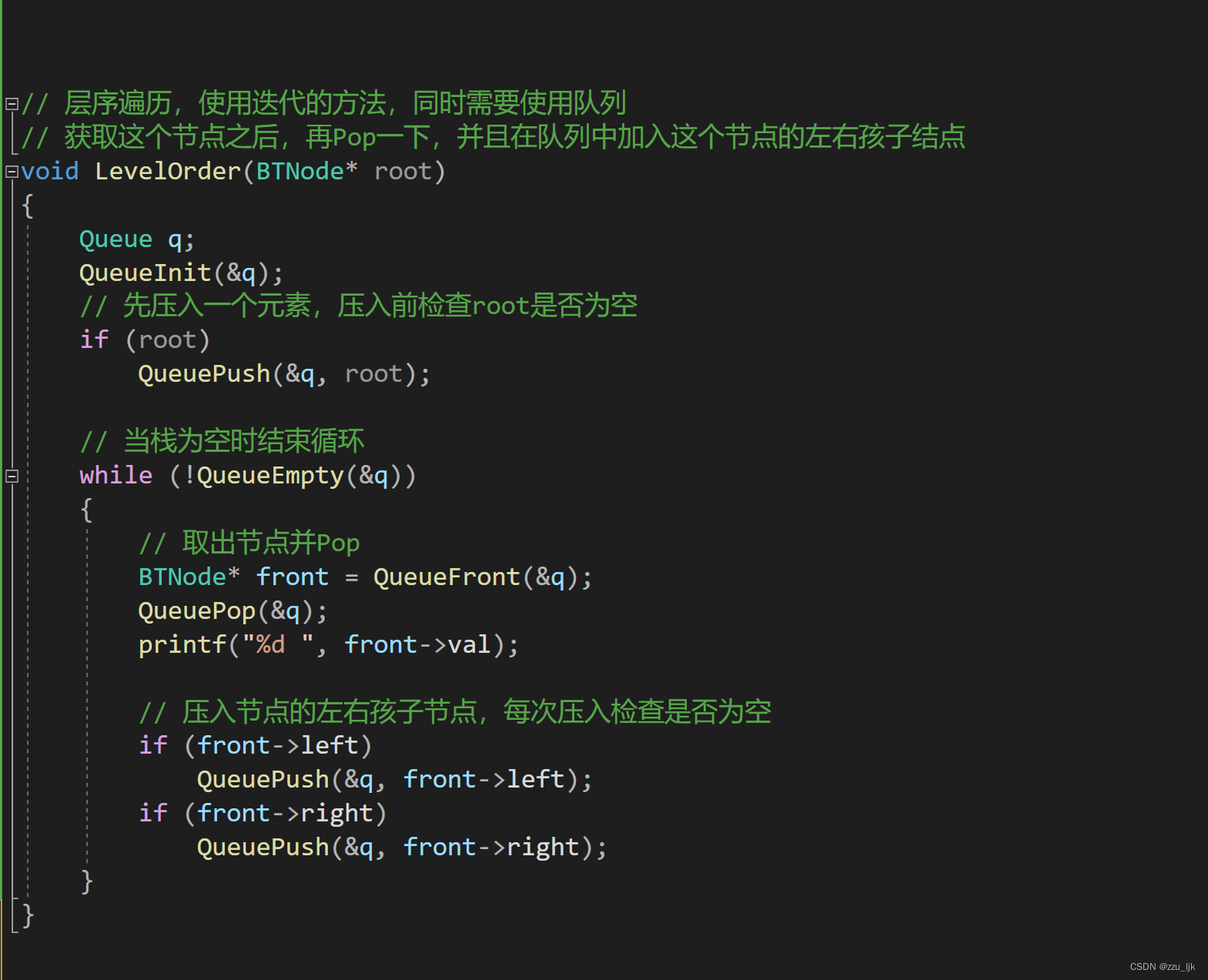
获取节点个数

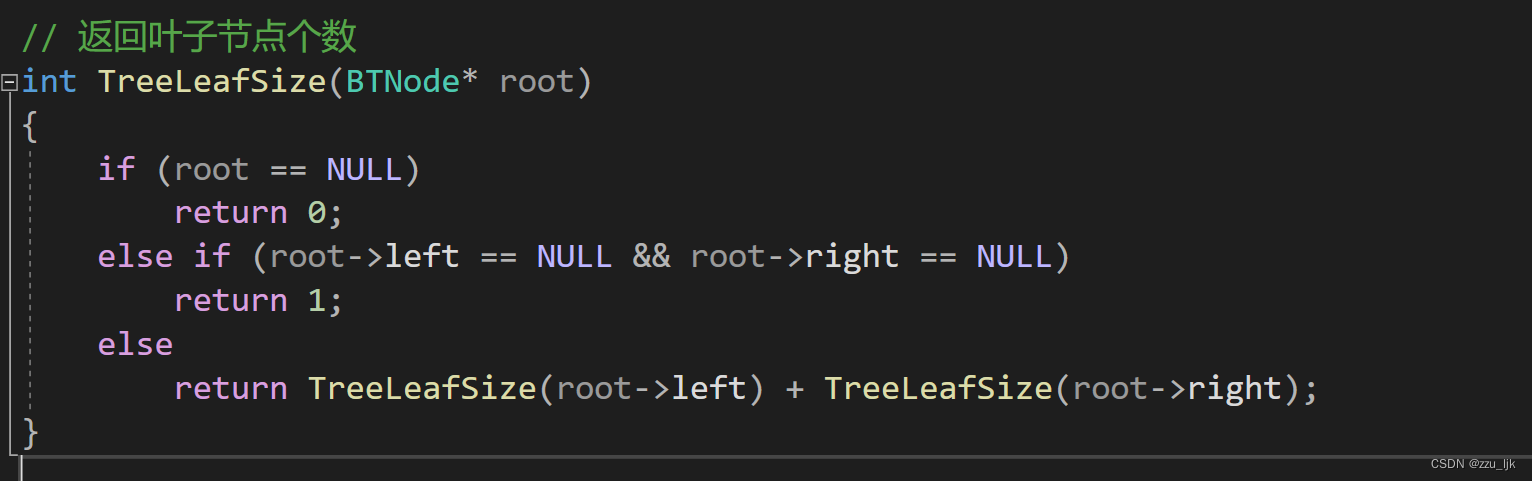
获取叶子节点个数

获取树的高度

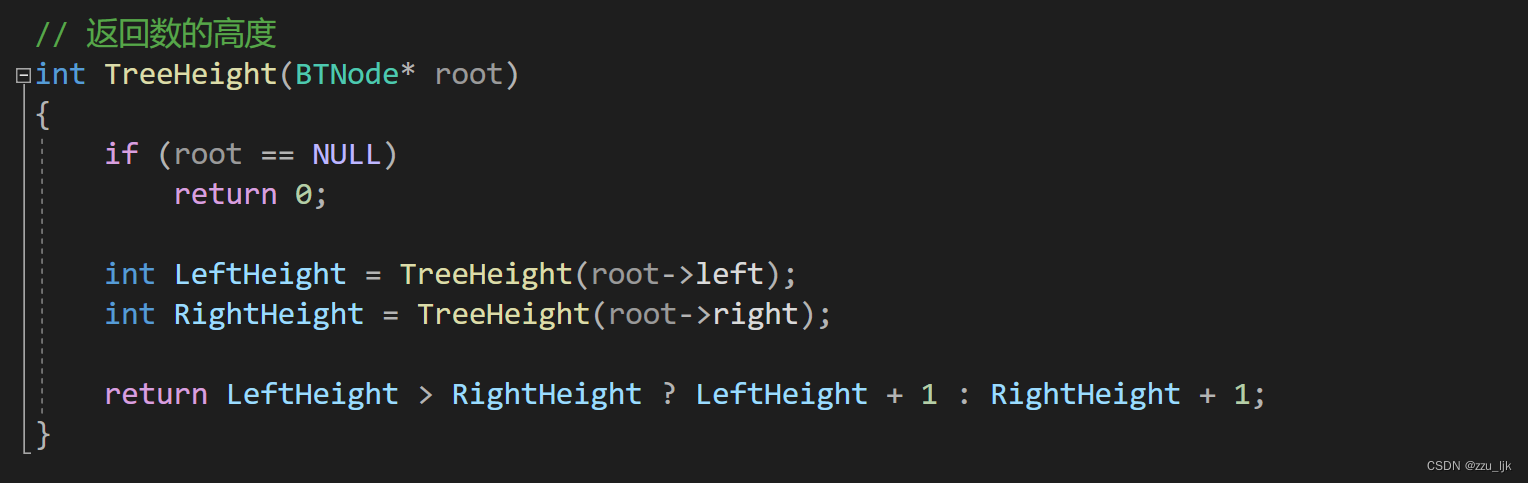
返回第K层节点个数

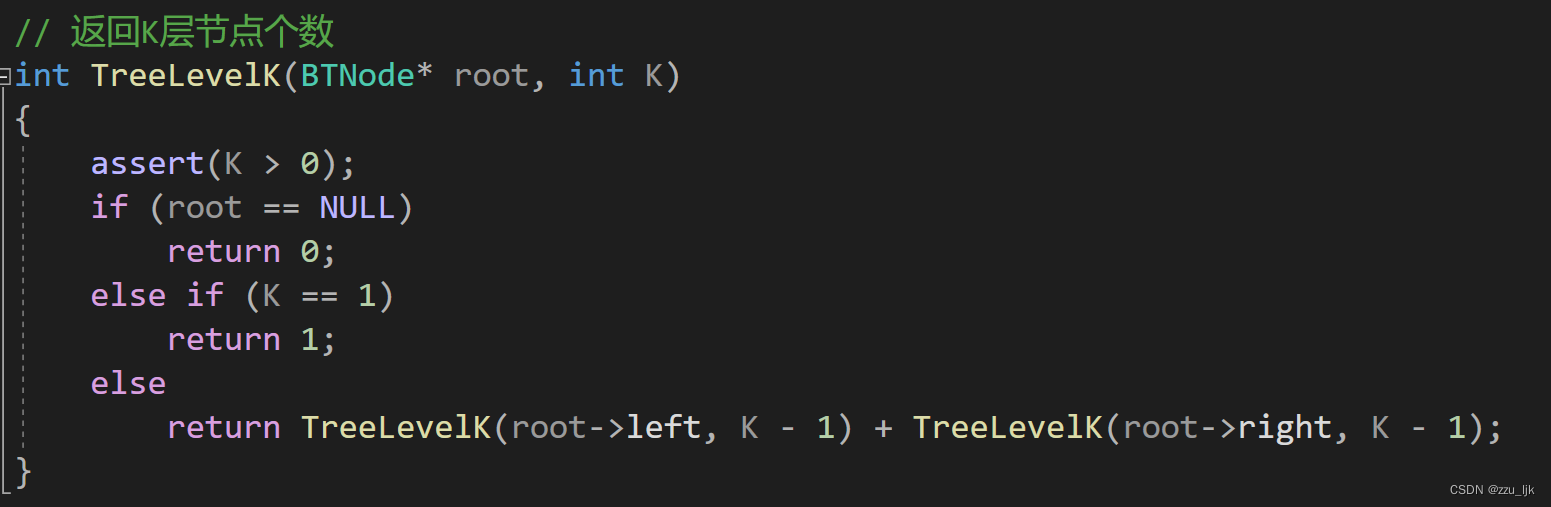
返回x所在节点

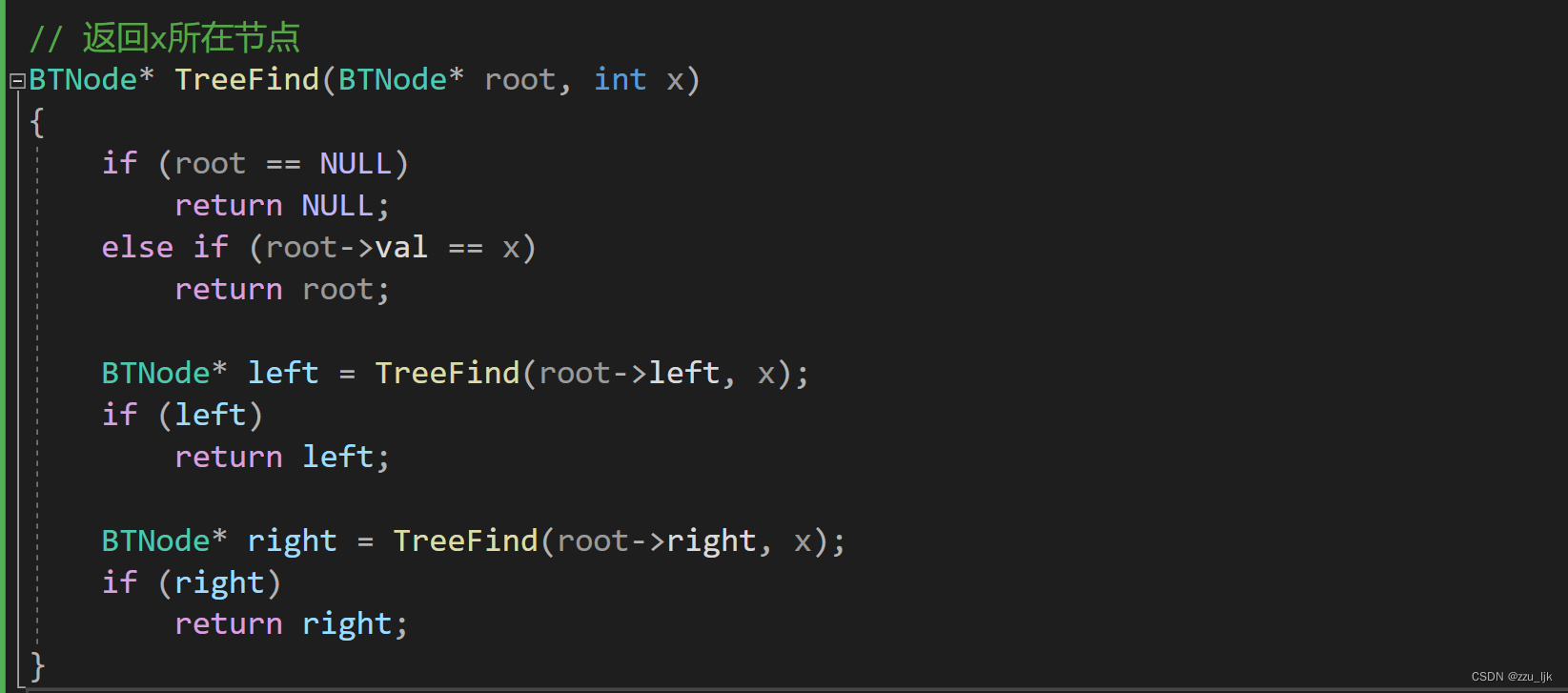
二叉树的销毁

OJ

单值二叉树

相同的树

对称二叉树

前序遍历

另一颗树的子树

二叉树的构建和遍历

二叉树知识点及选择题

N0 = N2 + 1

推导如下：

由中序和前序（或后序）确定结构的方法

如果是前序，正着看第一个就是根节点。把根节点确定之后看中序，找到中序中的根节点，在中序中在根节点左边的节点就在结构中根节点的左边，右边反之。这样确定之后再正着看前序，重复上面的逻辑。
如果是后序，反着看即可，最后一个节点即为根节点。

例题：已知某二叉树的中序遍历序列为JGDHKBAELIMCF，后序遍历序列为JGKHDBLMIEFCA，则其前序遍历序列为（ABDGJHKCEILMF ）

有N个元素的完全二叉树的深度是 logN + 1

如果是满二叉树，也可以说是log(N +1)

选择题：二叉树的最小深度

一颗拥有1000个结点的树度为4，则它的最小深度是（ 5 ）
解析：如果这棵树每一层都是满的，则它的深度最小，假设它为一个四叉树，高度为h，则这个数的节点个数为(4^h - 1) / 3，当h = 5, 最大节点数为341， 当h = 6, 最大节点数为1365，所以最小深度应该为6。

选择题：深度范围

设根结点的深度为1，则一个拥有n个结点的二叉树的深度一定在（ ）区间内
[log(n + 1)，n]

选择题：先序遍历序列与后序遍历序列正好相反

一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反，则该二叉树一定满足（ ）
前序遍历： 根 左 右
后序遍历： 左 右 根

若是前序和后序正好相反
则 根 右 左 = 根 左 右
说明右和左必有一个为空，即所有节点都是叶子节点