1.快速排序(双指针实现)
2.非递归实现快排
3.递归实现归并排序
4.非递归实现归并排序
5.总代码
1.快速排序(双指针实现)
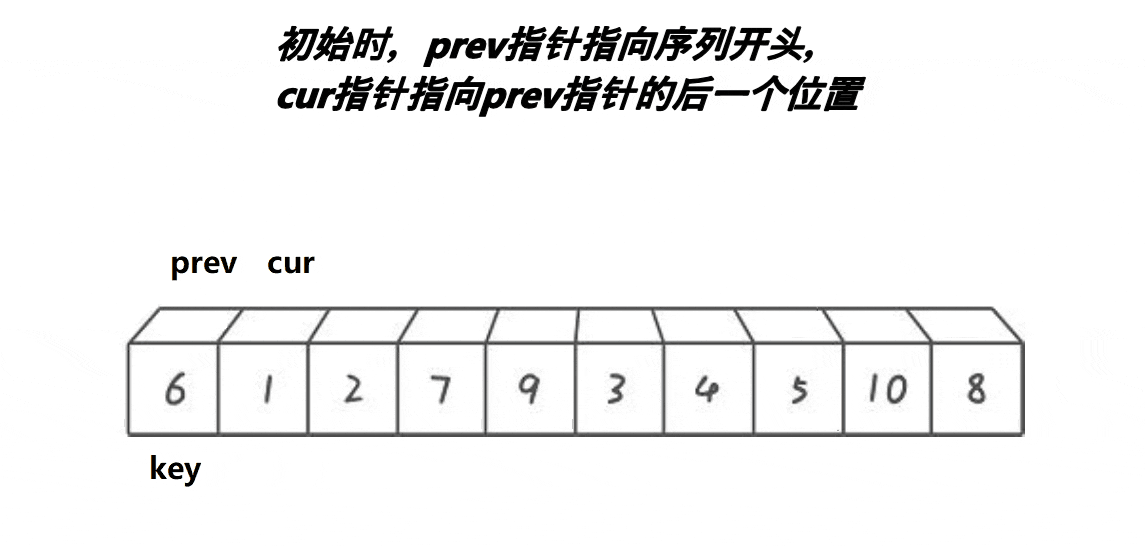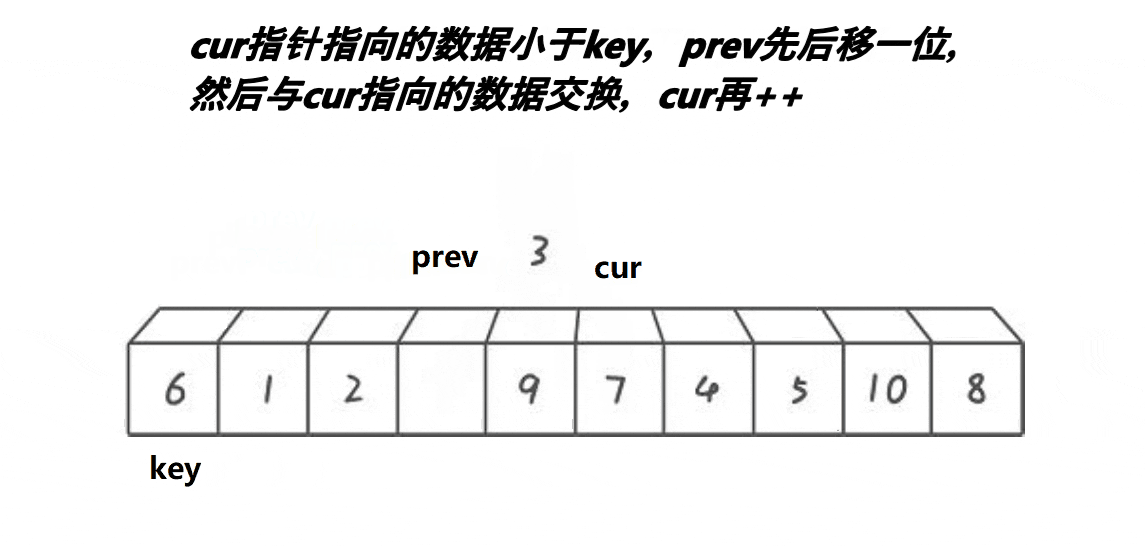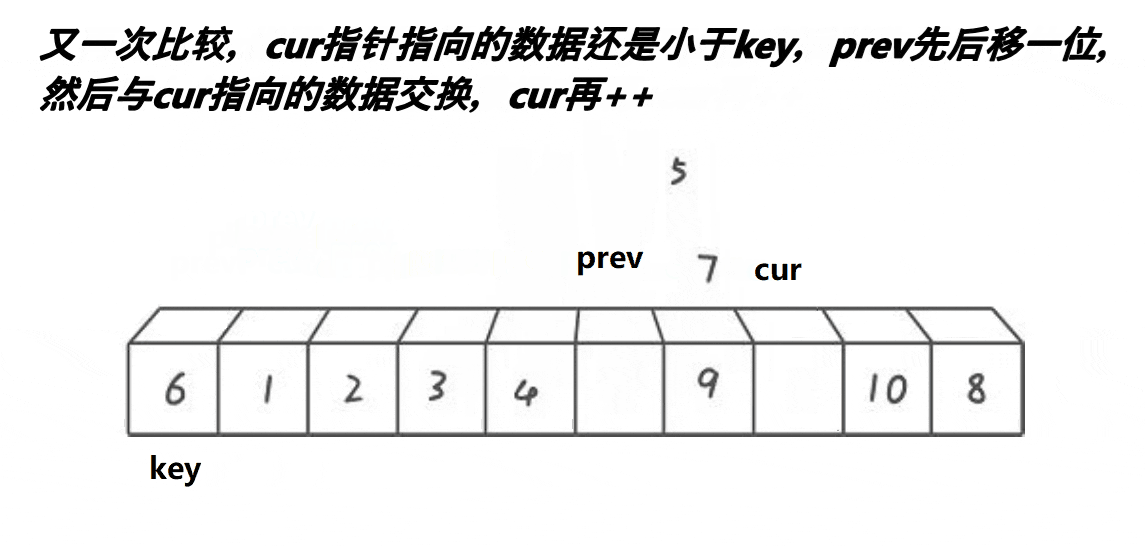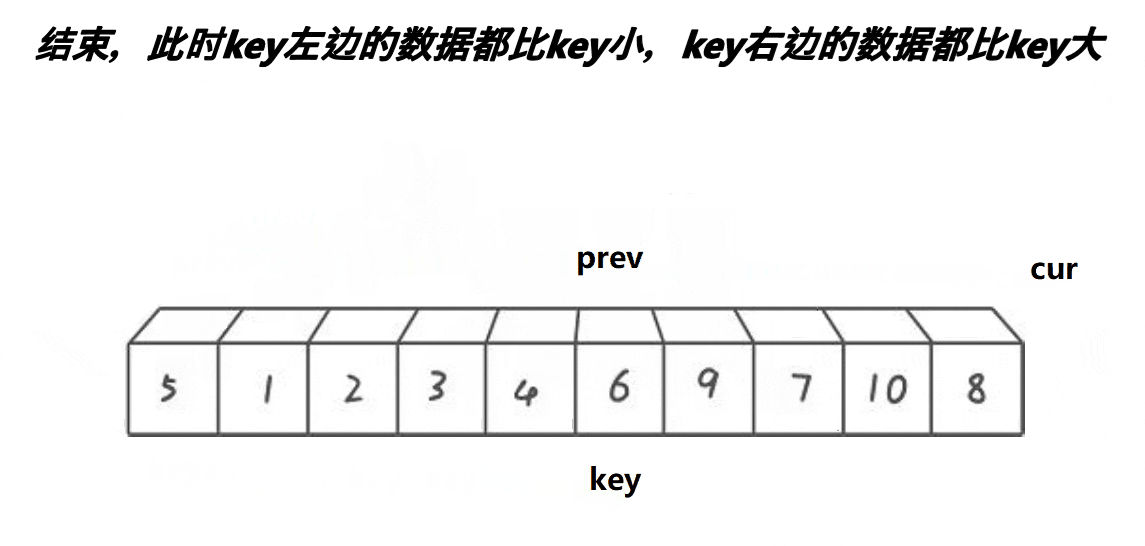
俩有个指针一前一后的排放着,cur先走并且去找比kye对应值小的数组值,一旦找到后prev就会往前一步然后与cur对应的值进行交换,直至cur走出数组,key对应的值与prev对应的值进行交换,第一躺就完成了,接下来用递归去走分支(排序中篇已经阐述过)去完成其它俩边的排序。
代码实现:
#include<stdio.h>
void swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void QuickSort2(int* a, int left,int right)
{
if (left >= right)
return;
int keyi = left;
int prev = left;
int cur = prev + 1;
/*while (cur<=right)
{
if (a[cur] < a[keyi])
{
++prev;
swap(&a[prev], &a[cur]);
}
++cur;
}*/代码1
while (cur <= right)
{
if (a[cur] <= a[keyi] && ++prev != cur)
swap(&a[prev], &a[cur]);
cur++;
}//代码2
swap(&a[keyi], &a[prev]);
QuickSort2(a, left, prev - 1);
QuickSort2(a, prev + 1, right);
}
int main()
{
int a[] = { 1,4,6,7,9,3,2,5,8,8,8,8,8,99 };
int size = sizeof(a) / sizeof(a[0]);
QuickSort2(a,0,size-1);
for (int i = 0; i < size; i++)
{
printf("%d ", a[i]);
}
return 0;
}代码分析:
循环的条件是cur小于等于right边界值才能一直执行,触发交换的条件是cur找到了比key小的值,这里有俩种写法,1是在里面++prev再交换,cur++之所以写在外面是因为不管你触不触发if都要加加,不然会死循环,
因为cur和prev会先重叠然后交互(前提是如果出门就发现了比key小的值) ,但如果prev和cur之间有距离差时就不会出现了,if的触发条件再加一个只有prev和cur不相等时才交换。

代码二则就相对简洁一些,在if判断里就可以实现prev++,但是需要注意的是判断++prev和cur是否相等要在后面,因为&&是前面满足才会看后面,如果写在前面就是不管找没找到都++prev,这样子prev就跑到cur前面去了,是不合理的,还有是pre停下来的位置是上一次交换完的位置,所以比keyi小,交换完后key的左边都是比key小,右边比key大。
2.非递归实现快排
快速排序用递归实现是相对简单的,但也可以使用非递归来实现。
首先要用到栈的知识,递归实现快排是一直开辟栈区来实现的,而开辟的栈区里面的内容有传过去的数组和left和right,但主要是left和right这俩个边界值,因为变的边界值,在每个开辟的栈区数组a都是同一个,但是边界值是不一样的,所以可以使用栈去存边界值left和right这俩个整型,然后用循环去更新边界值,每次从栈中取俩个值left和right,因为是单个单个放进去的,取也是单个单个取,每次获取边界值就跟递归一次效果差不多,但栈为空时就说明已经排好序了。
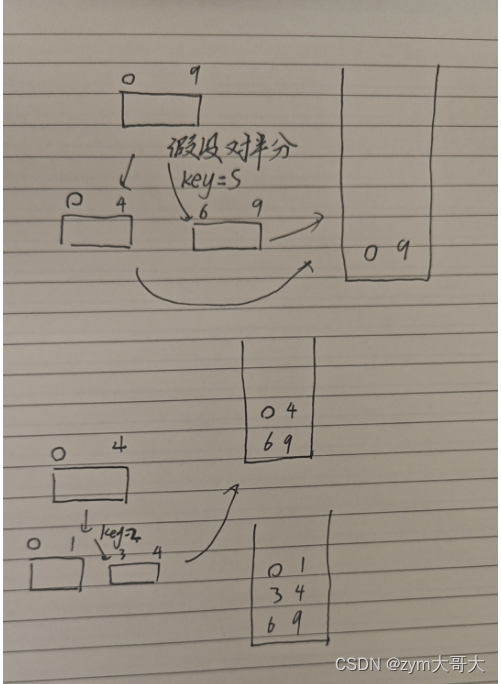
代码实现:
#include<stdio.h>
#include"Stack.h"
void swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
int PartSort2(int* a, int left, int right)
{
int keyi = left;
int prev = left;
int cur = prev + 1;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)
swap(&a[prev], &a[cur]);
cur++;
}
swap(&a[prev], &a[keyi]);
return prev;
}
void QuickSortNonR(int* a, int left, int right)
{
ST s;
STInit(&s);
STPush(&s, right);
STPush(&s, left);
while (!STEmpty(&s))
{
int begin = STTop(&s);
STPop(&s);
int end = STTop(&s);
STPop(&s);
int keyi = PartSort2(a, begin, end);
if (keyi + 1 < end)
{
STPush(&s,end);
STPush(&s, keyi + 1);
}
if (keyi - 1 > begin)
{
STPush(&s, keyi - 1);
STPush(&s, begin);
}
}
}
int main()
{
int a[] = { 9,8,7,6,5,4,3,3,2,1,55,66,0};
int size = sizeof(a) / sizeof(a[0]);
QuickSortNonR(a,0,size-1);
for (int i = 0; i < size; i++)
{
printf("%d ", a[i]);
}
return 0;
}代码分析:
先建立一个栈并初始化,然后把left和right放进去,这里循环的条件是栈是否为空,取出栈顶的俩个值,然后出栈俩次,把取出的值作为参数得到一个keyi值,再把keyi作为参考分出俩个新的区间,然后先判断新的区间是否满足条件,满足则就放入栈里面,这里是以前序去排序(深度优先遍历),队列也可以实现(广度优先遍历),但是在一些情况下是不满足的.
3.递归实现归并排序
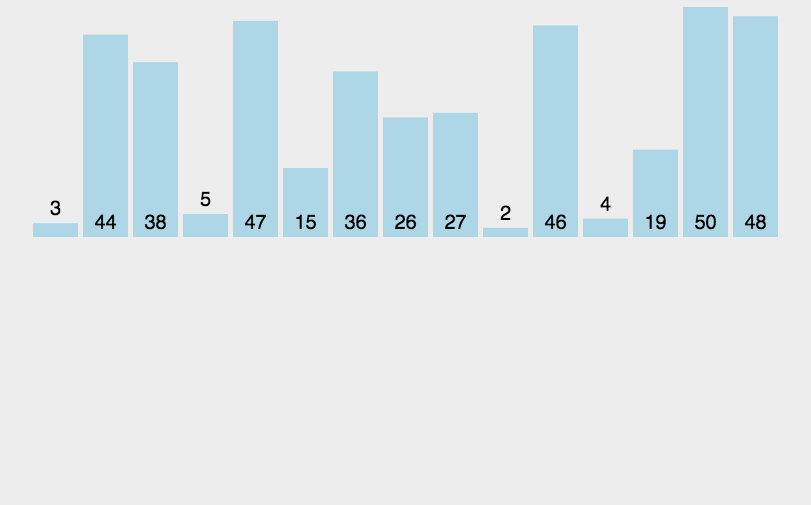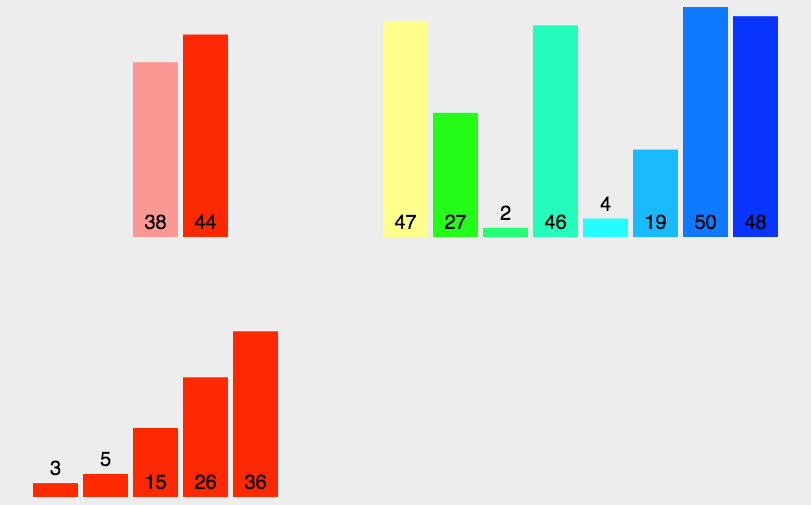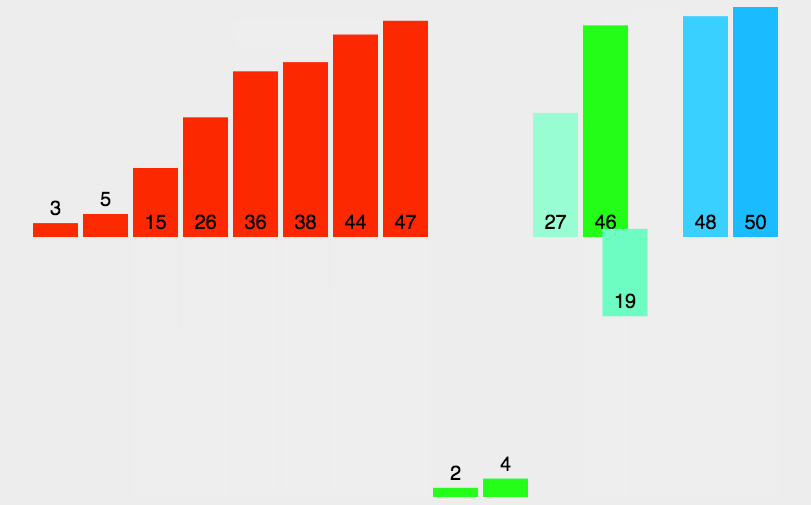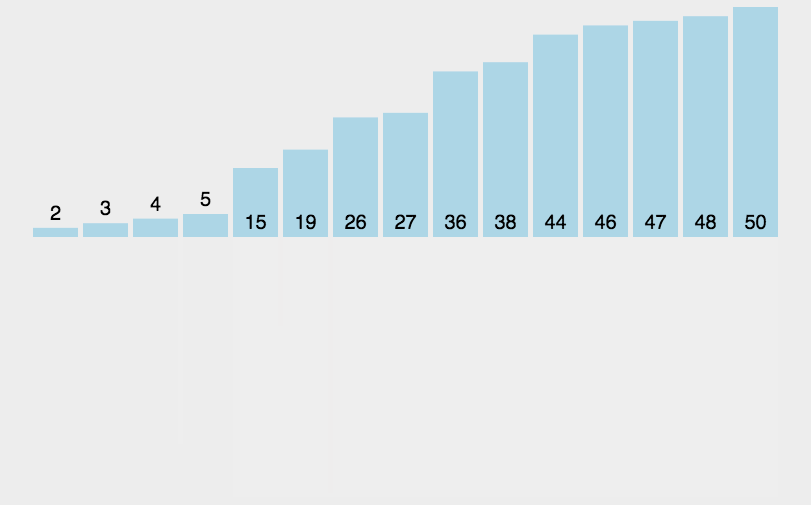
归并排序就是把一个数组对半分,一直分到只有一个,然后然后在俩个俩个比,比好就返回去,然后再俩个俩个比,此时俩个数是排好序的,比完后就变成个数为4的有序数组,然后在四个四个比,得到一个个数为8的有序数组,就是把整个分成若干个,在让这些小数组跟别的小数组比较合成一个新的有序数组,一直合成就变成与原来一样大的有序数组,就像魔方直接扣下来重新按颜色装好差不多。
代码实现:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
void _MergeSort(int* a, int* tmp, int left, int right)
{
if (left >= right)
return;
int mid = (left + right) / 2;
_MergeSort(a, tmp, left, mid);
_MergeSort(a, tmp, mid+1, right);
int begin1 = left,end1 = mid;//不能在逗号隔开后再加int
int begin2 = mid + 1,end2 = right;
int i = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while ( begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + left, tmp + left, (right - left + 1) * sizeof(int));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp==NULL)
{
perror("malloc fail:");
return;
}
_MergeSort(a, tmp, 0, n - 1);
free(tmp);
tmp=NULL;
}
int main()
{
int a[] = { 9,8,7,6,5,4,3,2,1 };
int size = sizeof(a) / sizeof(a[0]);
MergeSort(a, size);
for (int i = 0; i < size; i++)
{
printf("%d ", a[i]);
}
return 0;
}代码分析:
通过递归会把边界值一直缩小,直至长度为1,这是if条件会触发,不能再往下递归开始走后面的程序,此时边界是相等的(left=right),等于是二叉树的兄弟结点进行比大小,谁小谁在前面,俩俩比较,而最小面的俩个while是防止一个数组的值都比较小先放完了,但是还有数据没放完,因为是有序的,所以直接while依次放入,执行完后会返回去跟上一层次的兄弟结点比,最后到第二层时就是原来数组对半分,比完后合并则原来的数组就变成有序的。
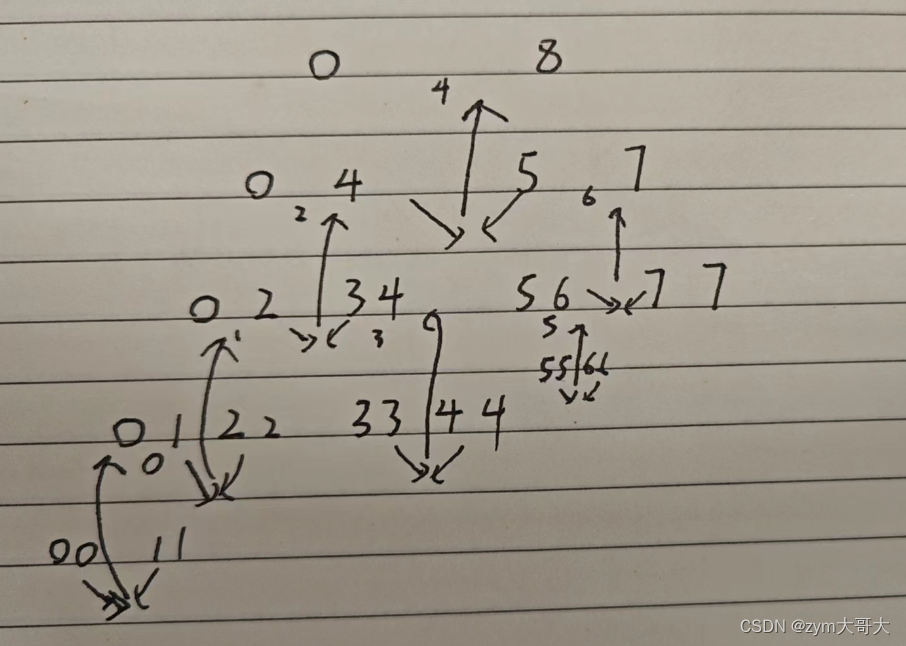
4.非递归实现归并排序
思想是通过循环来代替递归,先取gap组,俩俩gap个大小的进行比对后并放到tmp数组中,然后每次循环完后就改变区间到下一个区间去比较,end1-begin1=end2-begin2,但是有时候数组个数不一定能分均匀,有俩个if条件来判断,第一个if是俩个中有一个越界也就是不存在,所以不进行下面的合并,begin1是一定不会越界的,因为begin=i<n,所以只判断其他边界是否越界情况,end1越不越界不重要,要看后面的begin2是否越界,只要begin2越界了那么就不用合并了,第二个if则是判断end2有没有越界,越界了但是begin2没有,还有有效数据存在,所以要修正end2的值变为n-1,不让其越界访问,总的就是,用for循环来实现每俩个gap组能比较,while循环来控制gap的大小,来类比递归的效果。

代码实现:
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2*gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
int j = i;
if (begin2 >= n)//end1>n和end1小于n无所谓 只要begin2大于n就不用归并 俩个结果是一样的
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
//memcpy(a +begin1, tmp +begin1, sizeof(int) * (end2 - begin1 + 1));这样是不行的,因为在上面的代码中begin1已经不是原来的值了,
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
gap = 2*gap;
}
}
int main()
{
int a[] = { 9,8,7,6,5,4,3,2,1,4343,521,0,5,4,3,3 };
int size = sizeof(a) / sizeof(a[0]);
MergeSortNonR(a, size);
for (int i = 0; i < size; i++)
{
printf("%d ", a[i]);
}
return 0;
}5.归并排序的时间复杂度
因为每次会对半分,直到分成一个,所以能分成logn层,而每个层数访问数据个数都是n,所以总的时间复杂度就是O(N*logN),图片虽然是个三角形,但是每层个数都是n,这里的层数代表是分出的个数,可以理解为上面虽然比下面的短但是是一样重的。
总代码:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
void _MergeSort(int* a, int* tmp, int left, int right)
{
if (left >= right)
return;
int mid = (left + right) / 2;
_MergeSort(a, tmp, left, mid);
_MergeSort(a, tmp, mid+1, right);
int begin1 = left,end1 = mid;//不能在逗号隔开后再加int
int begin2 = mid + 1,end2 = right;
int i = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while ( begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + left, tmp + left, (right - left + 1) * sizeof(int));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp==NULL)
{
perror("malloc fail:");
return;
}
_MergeSort(a, tmp, 0, n - 1);
}
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2*gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
int j = i;
if (begin2 >= n)//end1>n和end1小于n无所谓 只要begin2大于n就不用归并 俩个结果是一样的
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
//memcpy(a +begin1, tmp +begin1, sizeof(int) * (end2 - begin1 + 1));这样是不行的,因为在上面的代码中begin1已经不是原来的值了,
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
gap = 2*gap;
}
}
int main()
{
int a[] = { 9,8,7,6,5,4,3,2,1,4343,521,0,5,4,3,3 };
int size = sizeof(a) / sizeof(a[0]);
MergeSortNonR(a, size);
for (int i = 0; i < size; i++)
{
printf("%d ", a[i]);
}
return 0;
}