目录
- 前言
- 一、计数排序
- 1.1 排序思想
- 1.2 代码
- 1.3 菜鸟教程官方代码(搬运)
- 二、基数排序
- 2.1 排序思想
- 2.2 代码
- 2.3 菜鸟教程官方代码(搬运)
- 三、桶排序
- 3.1 排序思想
- 3.2 代码
- 3.3 菜鸟教程官方代码(搬运)
前言
之前我们学过了几种常见的排序,都是基于比较的排序,我们也知道其中平均时间复杂度都是O(n * logn),要达到线性的时间复杂度,我们就需要新的排序方法!
接下来为大家介绍的三种排序方法都是不基于比较的排序!
一、计数排序
计数排序是一个非基于比较的排序算法,该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。 [1] 当然这是一种牺牲空间换取时间的做法,而且当O(k)>O(n * log(n))的时候其效率反而不如基于比较的排序(基于比较的排序的时间复杂度在理论上的下限是O(n * log(n)), 如归并排序,堆排序)
1.1 排序思想
计数的排序,对于每一个待排序的元素,如果知道待排序数组中有多少个比这个元素小的数,我们就可以直接知道在排序后的数组中该元素在什么位置上。
这就是计数排序的思想,是不是很简单呀?可是实现起来就有点难了!
步骤:
- 找出待排序的数组中最大和最小的元素
- 统计数组中每个值为i的元素出现的次数,存入用来计数的数组C的第i项
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
- 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1
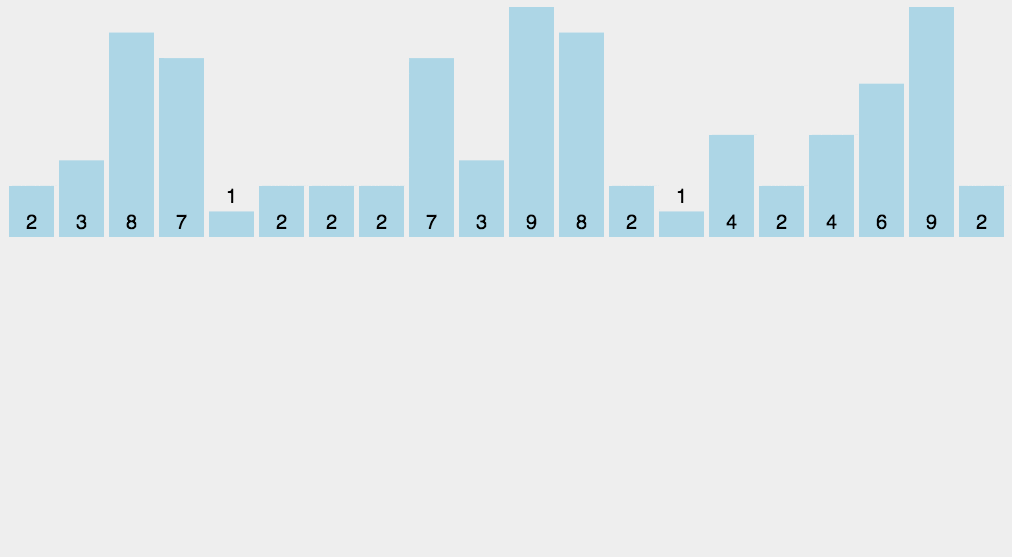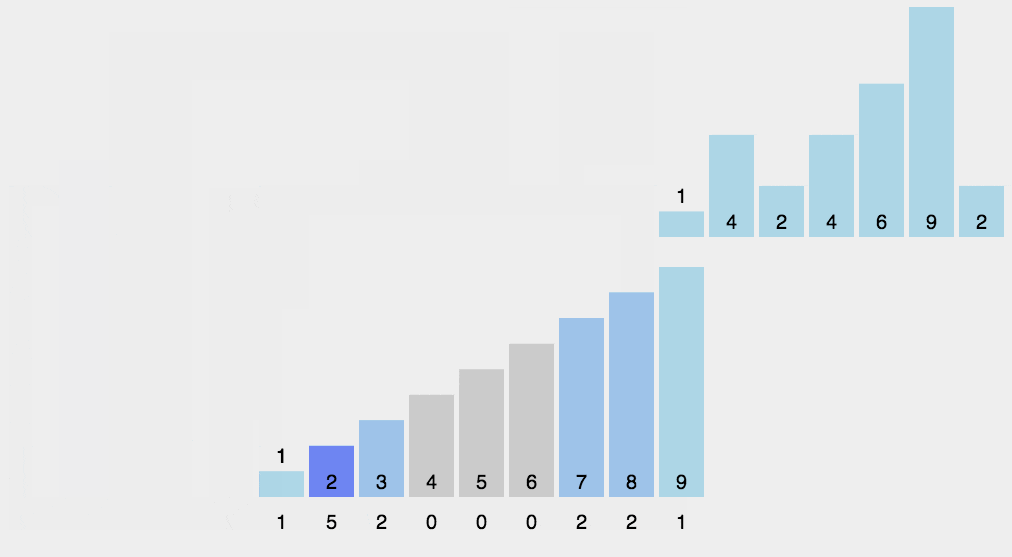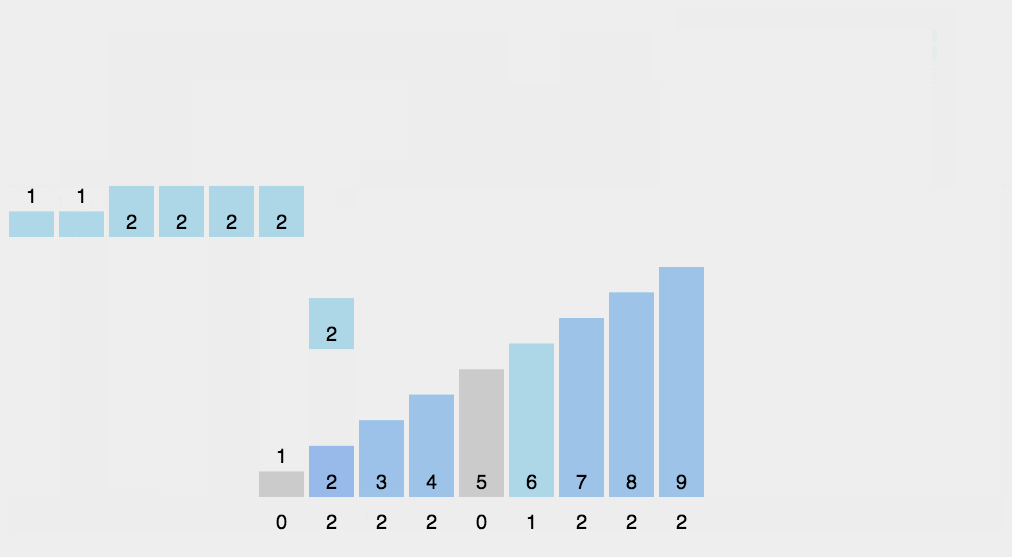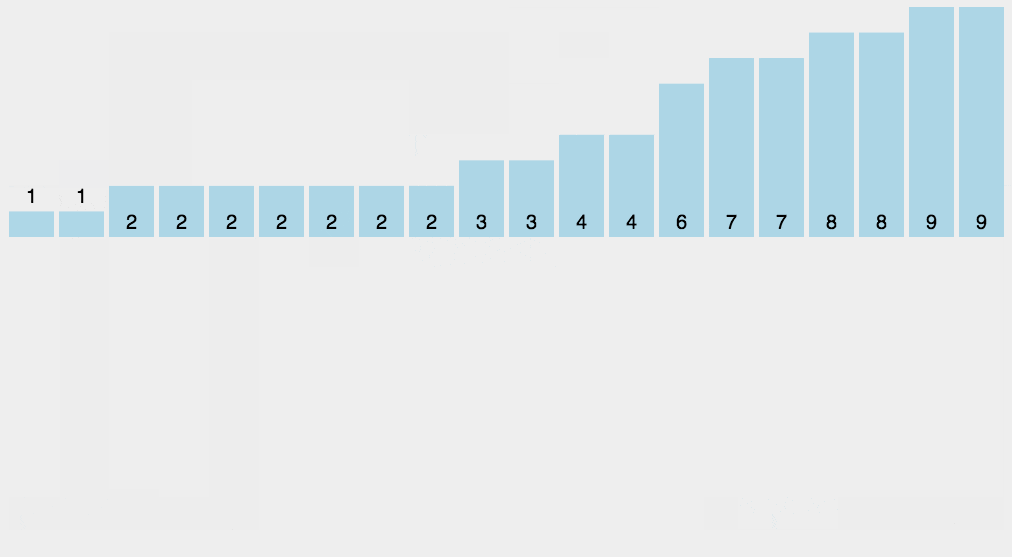
1.2 代码
/**
* 计数排序
* 一般适用于有n个数,数据范围是0-n之间
* @param array
*/
public static void countSort(int[] array) {
int maxVal = array[0];
int minVal = array[0];
for (int i = 0; i < array.length; i++) {
if (array[i] < minVal) {
minVal = array[i];
}
if (array[i] > maxVal) {
maxVal = array[i];
}
}
// 此处,说明已经找到了最大值和最小值
int[] count = new int[maxVal - minVal + 1];
// 统计array数组当中,每个数据出现的次数
for (int i = 0; i < array.length; i++) {
int index = array[i];
count[index - minVal]++;
}
// 接下来,只需要,遍历计数数组,把数据写回array
int indexArray = 0;
for (int i = 0; i < count.length; i++) {
while (count[i] > 0) {
// 这里一定要加minVal,因为不一定就是i出现了count[i]
array[indexArray] = i + minVal;
count[i]--;// 拷贝一个之后,次数也就少一个
indexArray++;// 下标得向后移动
}
}
}
1.3 菜鸟教程官方代码(搬运)
public class CountingSort implements IArraySort {
@Override
public int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
int maxValue = getMaxValue(arr);
return countingSort(arr, maxValue);
}
private int[] countingSort(int[] arr, int maxValue) {
int bucketLen = maxValue + 1;
int[] bucket = new int[bucketLen];
for (int value : arr) {
bucket[value]++;
}
int sortedIndex = 0;
for (int j = 0; j < bucketLen; j++) {
while (bucket[j] > 0) {
arr[sortedIndex++] = j;
bucket[j]--;
}
}
return arr;
}
private int getMaxValue(int[] arr) {
int maxValue = arr[0];
for (int value : arr) {
if (maxValue < value) {
maxValue = value;
}
}
return maxValue;
}
}
二、基数排序
基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些“桶”中,藉以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O (nlog(r )m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。
2.1 排序思想
基数排序整体来看是一种“分配和收集”排序,其将序列中的元素按照位数进行划分,不够的补0,将相同位数的元素先分配,分配后相同位数的元素排好序后,进行收集,重复该操作,可以完成排序。也可以这样理解,基数排序使用的是一种分治思想,对序列中相同位数的元素进行计数排序,所有的位数循环完成,则排序完成。
- 获取序列中的最大值,获取其长度length
- 新建一个二维数组用于模拟桶存放数据,取临时变量temp=1
- 循环的次数为length,新建数组count,用于保存各个桶中元素的个数,遍历原序列,序列中的元素先除以temp,再对10取余则可以得到,元素中个位数的值,将其放入各自编号的桶中,遍历结束,遍历count将排完序的数据放入到原数组中正确的位置,以此类推获取百位数,千位数,直到length循环结束。

2.2 代码
public static void radixSort(int[] array) {
if (array == null || array.length == 0) {
return;
}
// 获取最大值
int maxVal = array[0];
for (int i = 0; i < array.length; i++) {
if (array[i] > maxVal) {
maxVal = array[i];
}
}
// 用二维数组模拟桶放入东西,一共10个桶
int[][] tmp = new int[10][array.length];
// 元素最大值的长度
String maxString = maxVal + "";
int len = maxString.length();
int tmp1 = 1;
for (int i = 0; i < len; i++) {
// 用于记录每个桶中放入元素的位置
int[] count = new int[10];
for (int j = 0; j < array.length; j++) {
int a = (array[j] / tmp1) % 10;
tmp[a][count[a]] = array[j];
count[a]++;
}
tmp1 *= 10;
// 将数据取出放入原数组
int ret = 0;
for (int j = 0; j < count.length; j++) {
for (int k = 0; k < count[j]; k++) {
array[ret++] = tmp[i][j];
}
}
}
}
2.3 菜鸟教程官方代码(搬运)
/**
* 基数排序
* 考虑负数的情况还可以参考: https://code.i-harness.com/zh-CN/q/e98fa9
*/
public class RadixSort implements IArraySort {
@Override
public int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
int maxDigit = getMaxDigit(arr);
return radixSort(arr, maxDigit);
}
/**
* 获取最高位数
*/
private int getMaxDigit(int[] arr) {
int maxValue = getMaxValue(arr);
return getNumLenght(maxValue);
}
private int getMaxValue(int[] arr) {
int maxValue = arr[0];
for (int value : arr) {
if (maxValue < value) {
maxValue = value;
}
}
return maxValue;
}
protected int getNumLenght(long num) {
if (num == 0) {
return 1;
}
int lenght = 0;
for (long temp = num; temp != 0; temp /= 10) {
lenght++;
}
return lenght;
}
private int[] radixSort(int[] arr, int maxDigit) {
int mod = 10;
int dev = 1;
for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
// 考虑负数的情况,这里扩展一倍队列数,其中 [0-9]对应负数,[10-19]对应正数 (bucket + 10)
int[][] counter = new int[mod * 2][0];
for (int j = 0; j < arr.length; j++) {
int bucket = ((arr[j] % mod) / dev) + mod;
counter[bucket] = arrayAppend(counter[bucket], arr[j]);
}
int pos = 0;
for (int[] bucket : counter) {
for (int value : bucket) {
arr[pos++] = value;
}
}
}
return arr;
}
/**
* 自动扩容,并保存数据
*
* @param arr
* @param value
*/
private int[] arrayAppend(int[] arr, int value) {
arr = Arrays.copyOf(arr, arr.length + 1);
arr[arr.length - 1] = value;
return arr;
}
}
三、桶排序
桶排序 (Bucket sort)或所谓的箱排序,是一个排序算法,工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序)。桶排序是鸽巢排序的一种归纳结果。当要被排序的数组内的数值是均匀分配的时候,桶排序使用线性时间(Θ(n))。但桶排序并不是 比较排序,他不受到 O(n log n) 下限的影响。
3.1 排序思想
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效,我们需要做到这两点:
- 在额外空间充足的情况下,尽量增大桶的数量
- 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中
同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要。
3.2 代码
public static void bucketSort(int[] array) {
ArrayList bucket[] = new ArrayList[5]; // 声明5个桶
for (int i = 0; i < bucket.length; i++) {
bucket[i] = new ArrayList<Integer>(); // 确定桶的格式为ArrayList
}
for (int i = 0; i < array.length; i++) {
int index = array[i] / 10; // 确定元素存放的桶号
bucket[index].add(array[i]); // 将元素存入对应的桶中
}
for (int i = 0; i < bucket.length; i++) {
bucket[i].sort(null); // 对每一个桶排序
for (int j = 0; j < bucket[i].size(); j++) { // 遍历桶中的元素并输出
System.out.println(bucket[i].get(j) + " ");
}
}
}
3.3 菜鸟教程官方代码(搬运)
public class BucketSort implements IArraySort {
private static final InsertSort insertSort = new InsertSort();
@Override
public int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
return bucketSort(arr, 5);
}
private int[] bucketSort(int[] arr, int bucketSize) throws Exception {
if (arr.length == 0) {
return arr;
}
int minValue = arr[0];
int maxValue = arr[0];
for (int value : arr) {
if (value < minValue) {
minValue = value;
} else if (value > maxValue) {
maxValue = value;
}
}
int bucketCount = (int) Math.floor((maxValue - minValue) / bucketSize) + 1;
int[][] buckets = new int[bucketCount][0];
// 利用映射函数将数据分配到各个桶中
for (int i = 0; i < arr.length; i++) {
int index = (int) Math.floor((arr[i] - minValue) / bucketSize);
buckets[index] = arrAppend(buckets[index], arr[i]);
}
int arrIndex = 0;
for (int[] bucket : buckets) {
if (bucket.length <= 0) {
continue;
}
// 对每个桶进行排序,这里使用了插入排序
bucket = insertSort.sort(bucket);
for (int value : bucket) {
arr[arrIndex++] = value;
}
}
return arr;
}
/**
* 自动扩容,并保存数据
*
* @param arr
* @param value
*/
private int[] arrAppend(int[] arr, int value) {
arr = Arrays.copyOf(arr, arr.length + 1);
arr[arr.length - 1] = value;
return arr;
}
}