一、前言

本文主要讲了逆序对问题、归并排序法、树状数组与离散化处理，并讨论了一道例题。

二、逆序对问题

【题目描述】

给定一个序列 A1, ......, An。若 i<j 且 Ai>Aj，则 <i,j> 就是为一个“逆序对"。请你写一个程序，在尽量短的时间内统计出”逆序对“的数目。

【输入格式】

第 1 行是整数 n（1≤n≤500000），接下来1行，n个整数。

【输出格式】

一个整数，为逆序对的数目。

【输入样例】

6

5 4 2 6 3 1

【输出样例】

11

1、暴力法

模拟：先检查第一个数 a1，把后面所有数跟它比较，如果发现有一个比 a1小，就是一个逆序对；再检查第二个数，第三个数……；直到最后一个数。

复杂度：O(n^2)。

本题 n 最大 10^5，暴力法 TLE

n=int(input())
a=list(map(int,input().split()))
res=0
for i in range(n):
    for j in range(i+1,n):
        if a[j]<a[i]:
            res+=1
print(res)

2、归并排序法

观察暴力法的执行过程，发现和交换排序很像。

能否用交换排序的升级版归并排序，来处理逆序对问题?

那就试一试！

归并排序：

（1）分解。把初始序列分成长度相同的左右两个子序列，然后把每个子序列再分成更小的两个子序列……，直到子序列只包含1个数。用递归实现。

（2）合并。归并2个有序的子序列。

复杂度：

对n个数进行归并排序：

（1）需要 logn 趟归并；

（2）在每一趟归并中，有很多次合并操作，一共需要 O(n) 次比较。

复杂度：O(nlogn）

【归并排序和逆序对】

观察归并排序的一次合并过程，发现能利用这个过程来记录逆序对。

（1）在子序列内部，元素都是有序的，不存在逆序对；逆序对只存在于不同的子序列之间。

（2）合并两个子序列时：

如果前一个子序列的元素比后面子序列的元素小，无逆序对。

如果前一个子序列的元素比后面子序列的元素大，有逆序对，且有 mid-(i-1) 个（why mid-i+1，看下面代码可以知道）

def merge(L,mid,R):
    global res
    i=L
    j=mid+1
    t=0
    while i<=mid and j<=R:
        if a[i]>a[j]:       #前面部分大于后面部分的数值，说明是逆序对
            b[t]=a[j]
            t+=1
            j+=1
            res=res+mid-i+1     #记录逆序对数量
        else:
            b[t]=a[i]
            t+=1
            i+=1
    #一个子序列中的数都处理完了，另一个还没有，把剩下的复制过来
    while i<=mid:
        b[t]=a[i]
        t+=1
        i+=1
    while j<=R:
        b[t]=a[j]
        t+=1
        j+=1
    for i in range(t):
        a[L+i]=b[i]         #把排好序的b[]复制回a[]
            

def merge_sort(L,R):        #归并分治，你还记不记得hhh，用sort太多了(doge)
    if L<R:
        mid=(L+R)//2    #平分成两个子序列
        merge_sort(L,mid)
        merge_sort(mid+1,R)
        merge(L,mid,R)

n=int(input())
a=list(map(int,input().split()))
b=[0]*n
res=0
merge_sort(0,n-1)
print(res)

代码通俗易懂，不再作过多的赘述。

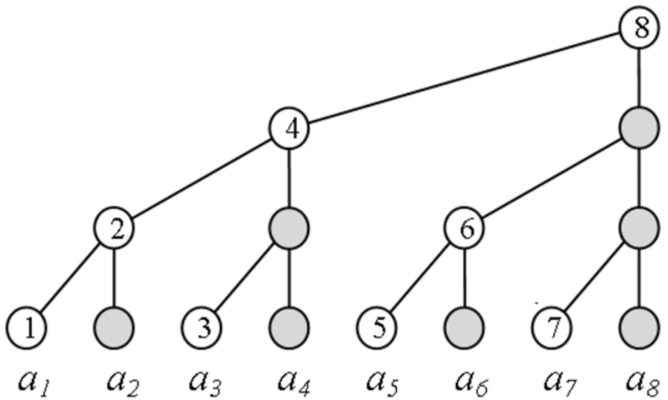
3、树状数组与逆序对（最巧妙最好的方法）

用树状数组求逆序对，是树状数组的巧妙应用，比其他方法都好。
用树状数组解逆序对：把数字看成树状数组的下标。
例如序列 {5, 4, 2, 6, 3, 1}，对应 a[5]、a[4]、a[2]、a[6]、a[3]、a[1]。
每处理一个数字，树状数组的下标所对应的元素数值加一，统计前缀和，就是逆序对的数量。
倒序或正序处理数据都行。

（1）倒序

用树状数组倒序处理数列，当前数字的前一个数的前缀和即为以该数为较大数的逆序对的个数。

例如 {5,4,2,6,3,1}，倒序处理数宇：

数字1。把 a[1] 加一，计算 a[1] 前面的前缀和 sum(0)，逆序对数量ans = ans + sum(0) = 0；

数字3。把 a[3] 加一，计算 a[3] 前面的前缀和 sum(2)，逆序对数量ans = ans + sum(2) = 1;

数字6。把 a[6] 加一，计算 a[6] 前面的前缀和 sum(5)，逆序对数量ans = ans + sum(5) = 1 + 2 = 3

（2）正序

当前已经处理的数字个数减掉当前数字的前缀和即为以该数为较小数的逆序对个数。

例如 {5,4,2,6,3,1}，正序处理数字：

数宇5。把 a[5] 加一，当前处理了 1 个数，ans = ans + (1-sum(5)) = 0;
数字4。把 a[4] 加一，当前处理了 2 个数，ans = ans + (2-sum(4)) = 0+1 = 1;
数宇2。把 a[2] 加一，ans = ans + (3-sum(2)) = 1+2 = 3;
数字6。把 a[6] 加一，ans = ans + (4-sum(6)) = 3+0 = 3;
等等

（3）离散化

上面的处理方法 “把数字看成树状数组的下标” 有个问题，如果数字比较大，例如数字等于 10^9，那么树状数组的空问也要开到 10^9=1G，远远超过了题目限制的空间。
用 “离散化” 这个小技巧能解决这个问题。

离散化：把原来的数字，用它们的相对大小来替换原来的数值，而它们的顺序仍然不变。
例：{1,20543,19,376,546007640}，它们的相对大小是{1,4,2,3,5}。
有多少个数字，离散化后的每个数字的大小就是多大。
在用树状数组求解逆序对的题目中，离散化几乎是必须的。
本题需处理 500000 个数字，离散化之后树状数组大小只需 500000。

【离散化方法1：重复数字离散化后不一样】

a=[1,20543,19,376,546007640,19]
print(a)
b=sorted(a)
print(b)
for i in range(len(b)):
    k=a.index(b[i])
    a[k]=i+1                #a[a.index(b[i])] = i+1
print(a)

【离散化方法2：重复数字离散化后也一样】

def discretization (h):
    b=list(set(h))
    b.sort()
    for i in range(len(h)) :
        h[i] = b.index(h[i])+1
a = [1,20543,19,376,546007640,19]
print(a)
discretization(a)
print(a)

【逆序对：树状数组代码】

def lowbit(x):
    return x&-x

def update(x,d):
    while x<=n:
        tree[x]+=d
        x+=lowbit(x)

def sum(x):
    ans=0
    while x>0:
        ans+=tree[x]
        x-=lowbit(x)
    return ans

n=int(input())
a=[0]+list(map(int,input().split()))        #从a[1]开始
b=sorted(a)
for i in range(n+1):
    a[a.index(b[i])]=i+1
tree=[0]*(n+1)
res=0
for i in range(len(a)-1,0,-1):
    update(a[i],1)
    res+=sum(a[i]-1)
print(res)

三、例题

1、小朋友排队（lanqiaoOJ题号222）

【题目描述】

n 个小朋友站成一排。现在要把他们按身高从低到高的顺序排列，但是每次只能交换位置相邻的两个小朋友。每个小朋友都有一个不高兴的程度。开始的时候，所有小朋友的不高兴程度都是 0。如果某个小朋友第一次被要求交换，则他的不高兴程度增加 1，如果第二次要求他交换，则他的不高兴程度增加 2（即不高兴程度为3），依次类推。

当要求某个小朋友第 k 次交换时，他的不高兴程度增加 k。请问，要让所有小朋友按从低到高排队，他们的不高兴程度之和最小是多少。如果有两个小朋友身高一样，则他们谁站在谁前面是没有关系的。

【输入格式】

输入的第一行包含一个整数 n，表示小朋友的个数。第二行包含 n 个整数 H1、H2、…、Hn，分别表示每个小朋友的身高。1<=n<=100000，0<=Hi<=1000000。

【输出格式】

输出一行，包含一个整数，表示小朋友的不高兴程度和的最小值。

每个小朋友要交换多少次？每一个小朋友最少的交换次数等于他左边比他高的人数加上右边比他矮的人数。

逆序对问题，包括2个逆序对：

（1）他左边比他高的人；

（2）右边比他矮的人。

用树状数组做两次逆序对，一次正序处理，一次倒序处理。

本题不需离散化。

def lowbit(x):
    return x&-x

def update(x,d):
    while x<=N:
        tree[x]+=d
        x+=lowbit(x)

def sum(x):
    ans=0
    while x>0:
        ans+=tree[x]
        x-=lowbit(x)
    return ans

N=1000010
n=int(input())
Hold=list(map(int,input().split()))
H=[0 for _ in range(N)]             #H是身高
for i in range(n):
    H[i+1] = Hold[i]+1

k=[0 for _ in range(N)]             #每个小朋友的最少交换次数．也是逆序对数量
tree=[0 for _ in range(N)]

for i in range(1,n+1):              #正序处理逆序对，右边矮的
    k[i]=sum(N-1)-sum(H[i])
    update(H[i],1)

tree=[0 for _ in range(N)]

for i in range(n,0,-1):              #倒序处理逆序对，左边高的
    k[i]+=sum(H[i]-1)
    update(H[i],1)

res=0
for i in range(1,n+1,1):
    res+=int((1+k[i])*k[i]/2)
print(res)

以上，逆序对问题、树状数组与离散化

祝好