布局

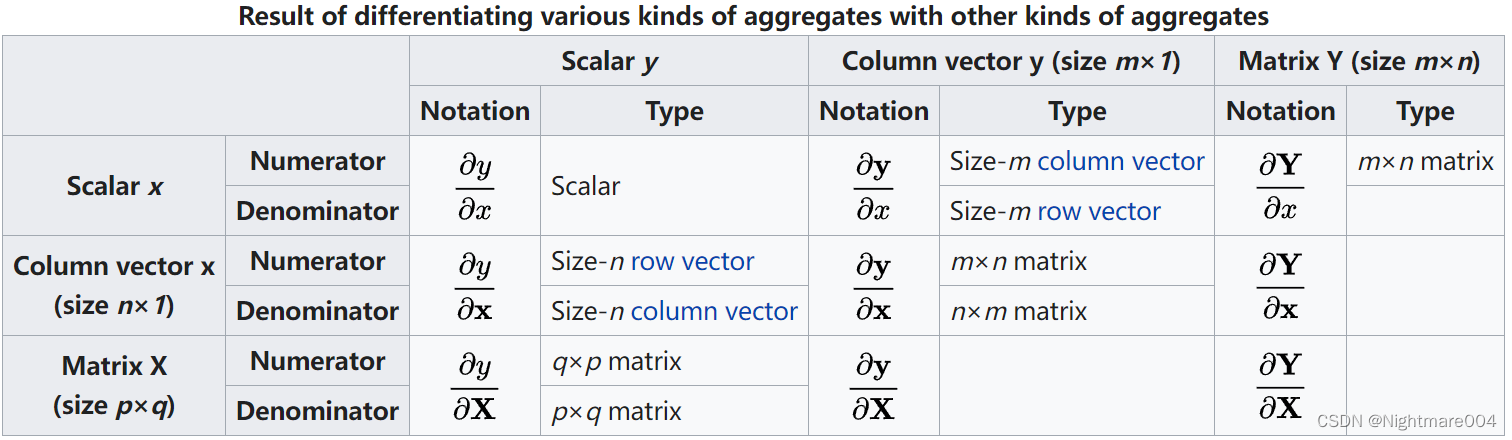
分子布局

$$\frac{\partial y}{\partial \mathbf{x}}=\left(\begin{array}{cccc}\frac{\partial y}{\partial x_1}& \frac{\partial y}{\partial x_2}& \cdots & \frac{\partial y}{\partial x_n}\end{array}\right)$$
$$\frac{\partial \mathbf{y}}{\partial x}=\left(\begin{array}{c}\frac{\partial y_1}{\partial x}\\ \frac{\partial y_2}{\partial x}\\ ⋮\\ \frac{\partial y_n}{\partial x}\end{array}\right)$$
$$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}=\left[\begin{array}{cccc}\frac{\partial y_1}{\partial x_1}& \frac{\partial y_1}{\partial x_2}& \cdots & \frac{\partial y_1}{\partial x_n}\\ \frac{\partial y_2}{\partial x_1}& \frac{\partial y_2}{\partial x_2}& \cdots & \frac{\partial y_2}{\partial x_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial y_m}{\partial x_1}& \frac{\partial y_m}{\partial x_2}& \cdots & \frac{\partial y_m}{\partial x_n}\end{array}\right]$$
$$\frac{\partial y}{\partial \mathbf{X}}=\left[\begin{array}{cccc}\frac{\partial y}{\partial x_{11}}& \frac{\partial y}{\partial x_{21}}& \cdots & \frac{\partial y}{\partial x_{p1}}\\ \frac{\partial y}{\partial x_{12}}& \frac{\partial y}{\partial x_{22}}& \cdots & \frac{\partial y}{\partial x_{p2}}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial y}{\partial x_{1q}}& \frac{\partial y}{\partial x_{2q}}& \cdots & \frac{\partial y}{\partial x_{pq}}\end{array}\right]$$
$$\frac{\partial \mathbf{Y}}{\partial x}=\left[\begin{array}{cccc}\frac{\partial y_{11}}{\partial x}& \frac{\partial y_{12}}{\partial x}& \cdots & \frac{\partial y_{1n}}{\partial x}\\ \frac{\partial y_{21}}{\partial x}& \frac{\partial y_{22}}{\partial x}& \cdots & \frac{\partial y_{2n}}{\partial x}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial y_{m1}}{\partial x}& \frac{\partial y_{m2}}{\partial x}& \cdots & \frac{\partial y_{mn}}{\partial x}\end{array}\right]$$
$$d\mathbf{X}=\left[\begin{array}{cccc}d{x}_{11}& d{x}_{12}& \cdots & d{x}_{1n}\\ d{x}_{21}& d{x}_{22}& \cdots & d{x}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ d{x}_{m1}& d{x}_{m2}& \cdots & d{x}_{mn}\end{array}\right]$$

分母布局

$$\frac{\partial y}{\partial \mathbf{x}}=\left[\begin{array}{c}\frac{\partial y}{\partial x_1}\\ \frac{\partial y}{\partial x_2}\\ ⋮\\ \frac{\partial y}{\partial x_n}\end{array}\right]$$
$$\frac{\partial \mathbf{y}}{\partial x}=\left[\begin{array}{llll}\frac{\partial y_1}{\partial x}& \frac{\partial y_2}{\partial x}& \cdots & \frac{\partial y_m}{\partial x}\end{array}\right]$$
$$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}=\left[\begin{array}{cccc}\frac{\partial y_1}{\partial x_1}& \frac{\partial y_2}{\partial x_1}& \cdots & \frac{\partial y_m}{\partial x_1}\\ \frac{\partial y_1}{\partial x_2}& \frac{\partial y_2}{\partial x_2}& \cdots & \frac{\partial y_m}{\partial x_2}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial y_1}{\partial x_n}& \frac{\partial y_2}{\partial x_n}& \cdots & \frac{\partial y_m}{\partial x_n}\end{array}\right]$$
$$\frac{\partial y}{\partial \mathbf{X}}=\left[\begin{array}{cccc}\frac{\partial y}{\partial x_{11}}& \frac{\partial y}{\partial x_{12}}& \cdots & \frac{\partial y}{\partial x_{1q}}\\ \frac{\partial y}{\partial x_{21}}& \frac{\partial y}{\partial x_{22}}& \cdots & \frac{\partial y}{\partial x_{2q}}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial y}{\partial x_{p1}}& \frac{\partial y}{\partial x_{p2}}& \cdots & \frac{\partial y}{\partial x_{pq}}\end{array}\right]$$

向量对向量求导

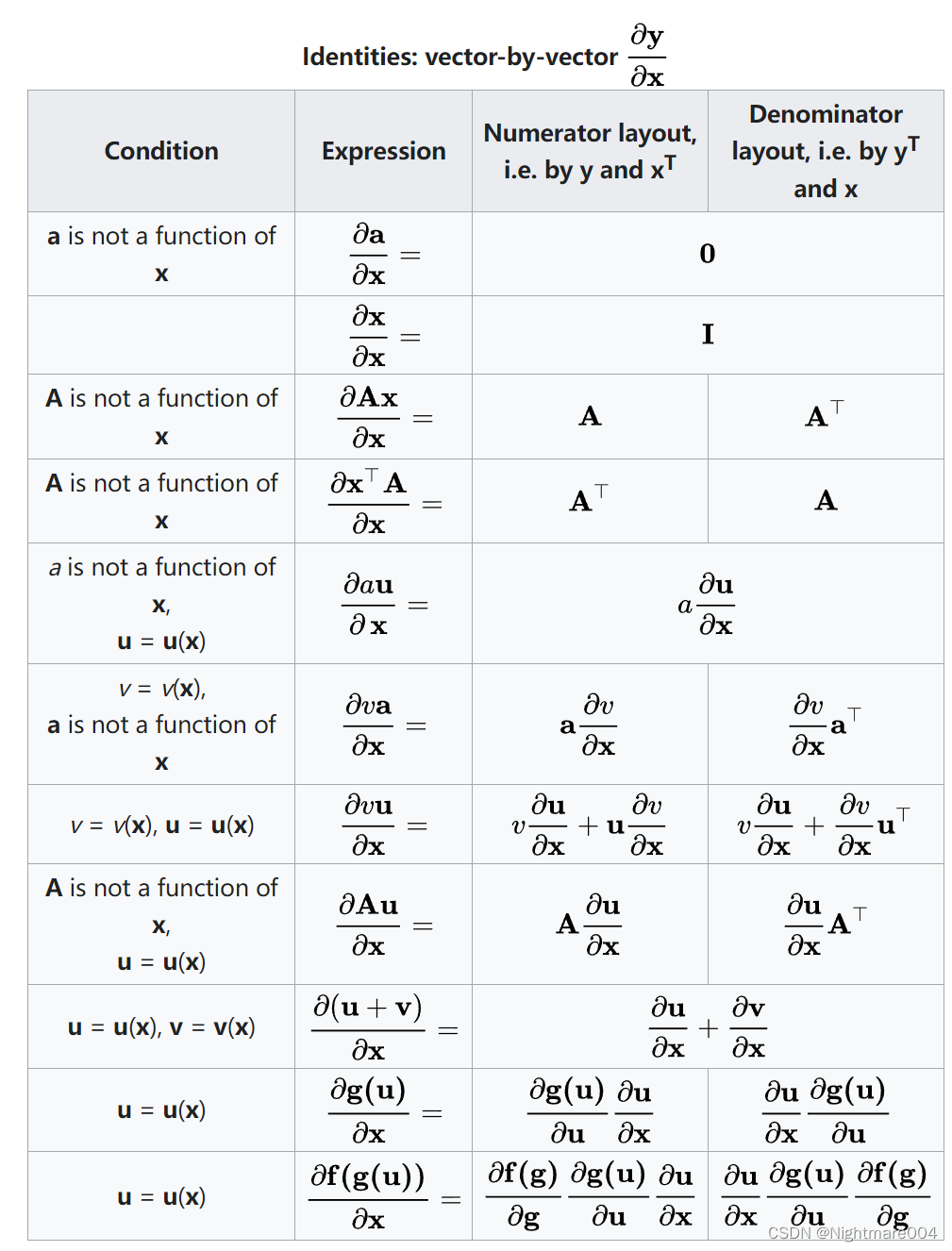
推导1：
设$v=v\left(\mathbf{x}\right),\mathbf{u}=\mathbf{u}\left(\mathbf{x}\right)$
$\frac{\partial v\mathbf{u}}{\partial \mathbf{x}}$
分子布局：
$\frac{\partial {\left(v\mathbf{u}\right)}_i}{\partial {\mathbf{x}}_j}=\frac{\partial \left(v{\mathbf{u}}_i\right)}{\partial {\mathbf{x}}_j}=\frac{\partial v}{\partial {\mathbf{x}}_j}{\mathbf{u}}_i+v\frac{\partial {\mathbf{u}}_i}{\partial {\mathbf{x}}_j}={\mathbf{u}}_i{\left(\frac{\partial v}{\partial \mathbf{x}}\right)}_j+v{\left(\frac{\partial \mathbf{u}}{\partial \mathbf{x}}\right)}_{ij}$
进而
$\frac{\partial v\mathbf{u}}{\partial \mathbf{x}}=\mathbf{u}\frac{\partial v}{\partial \mathbf{x}}+v\frac{\partial \mathbf{u}}{\partial \mathbf{x}}$

分母布局：
$\frac{\partial {\left(v\mathbf{u}\right)}_j}{\partial {\mathbf{x}}_i}=\frac{\partial \left(v{\mathbf{u}}_j\right)}{\partial {\mathbf{x}}_i}=\frac{\partial v}{\partial {\mathbf{x}}_i}{\mathbf{u}}_j+v\frac{\partial {\mathbf{u}}_j}{\partial {\mathbf{x}}_i}={\left(\frac{\partial v}{\partial \mathbf{x}}\right)}_i{\mathbf{u}}_j+v{\left(\frac{\partial \mathbf{u}}{\partial \mathbf{x}}\right)}_{ij}$
$\frac{\partial v\mathbf{u}}{\partial \mathbf{x}}=\frac{\partial v}{\partial \mathbf{x}}{\mathbf{u}}^T+v\frac{\partial \mathbf{u}}{\partial \mathbf{x}}$

推导2：
设$\mathbf{g}\left(\mathbf{u}\right):{\mathbb{R}}^n\to {\mathbb{R}}^n$
则$\frac{\partial g_i}{\partial x_j}={\sum }_k\frac{\partial g_i}{\partial u_k}\frac{\partial u_k}{\partial x_j}$
分子布局：$\frac{\partial \mathbf{g}}{\partial \mathbf{x}}=\frac{\partial \mathbf{g}}{\partial \mathbf{u}}\frac{\partial \mathbf{u}}{\partial \mathbf{x}}$

例子：
$l=\Vert \mathbf{Xw}-\mathbf{y}{\Vert }^2$,其中$\mathbf{X}\in {\mathbb{R}}^{m\times n},\mathbf{w},\mathbf{y}\in {\mathbb{R}}^n$,求$\frac{\partial l}{\partial \mathbf{w}}$
设$\mathbf{u}=\mathbf{Xw}-\mathbf{y}$
$$\frac{\partial l}{\partial \mathbf{w}}=\frac{\partial \mathbf{u}}{\partial \mathbf{w}}\frac{\partial l}{\partial \mathbf{u}}={\mathbf{X}}^{T}2\mathbf{u}=2{\mathbf{X}}^T\left(\mathbf{Xw}-\mathbf{y}\right)$$

标量对向量求导

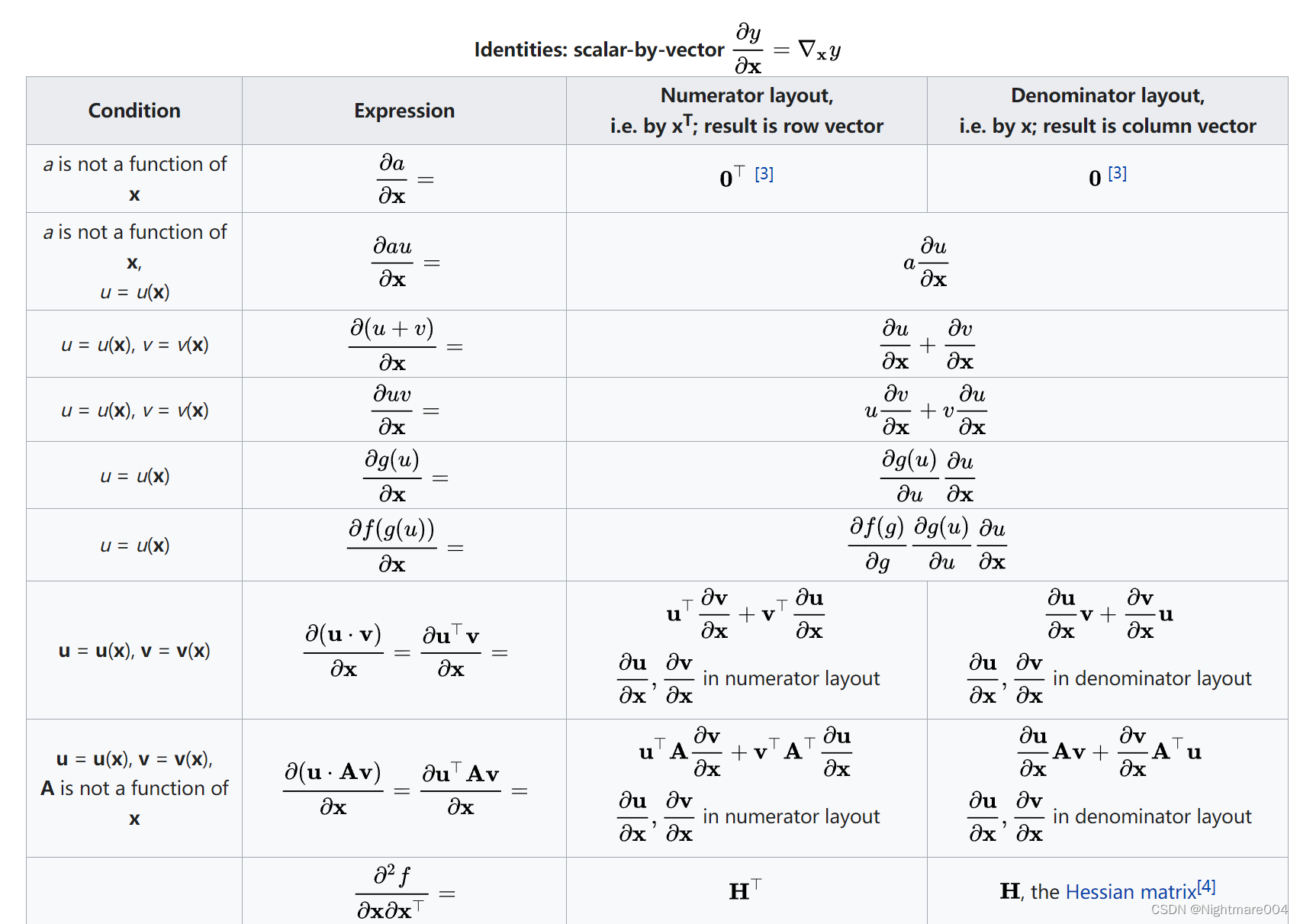
微分

分母布局
$$\mathrm{d}\mathrm{f}=\sum _{\mathrm{i}=1}^{\mathrm{m}}\sum _{\mathrm{i}=1}^{\mathrm{n}}\frac{\partial \mathrm{f}}{\partial {\mathrm{x}}_{\mathrm{ij}}}\mathrm{d}{\mathrm{x}}_{\mathrm{ij}}=\mathrm{tr}\left({\frac{\partial \mathrm{f}}{\partial \mathbf{x}}}^{\mathrm{T}}\mathrm{d}\mathbf{X}\right)$$
法则：
$\mathrm{d}\left(\mathbf{X}\pm \mathbf{Y}\right)=\mathrm{d}\mathbf{X}\pm \mathrm{d}\mathbf{Y}$
$\mathrm{d}\left(\mathbf{XY}\right)=\mathrm{d}\left(\mathbf{X}\right)\mathbf{Y}+\mathbf{X}\mathrm{d}\left(\mathbf{Y}\right)$
$\mathrm{d}\left({\mathbf{X}}^{\mathrm{T}}\right)={\left(\mathrm{d}\mathbf{X}\right)}^{\mathrm{T}}$
$\mathrm{d}\mathrm{tr}\left(\mathbf{X}\right)=\mathrm{tr}\left(\mathrm{d}\mathbf{X}\right)$
$\mathrm{d}{\mathbf{X}}^{-1}=-{\mathbf{X}}^{-1}\left(\mathrm{d}\mathbf{X}\right){\mathbf{X}}^{-1}$
$\mathrm{d}\left|\mathbf{X}\right|=\mathrm{tr}\left({\mathbf{X}}^{\ast }\mathrm{d}\mathbf{X}\right)=\left|\mathbf{X}\right|\mathrm{tr}\left({\mathbf{X}}^{-1}\mathrm{d}\mathbf{X}\right)$
$d(\mathbf{X}\odot \mathbf{Y})=d\mathbf{X}\odot \mathbf{Y}+\mathbf{X}\odot d\mathbf{Y}$
$d\sigma (\mathbf{X})={\sigma }^{\prime }(\mathbf{X})\odot d\mathbf{X}$

技巧：
$\mathbf{X}=tr\left(\mathbf{X}\right)$
$tr\left({\mathbf{X}}^T\right)=tr\left(\mathbf{X}\right)$
$tr\left(\mathbf{X}\pm \mathbf{Y}\right)=tr\left(\mathbf{X}\right)\pm tr\left(\mathbf{Y}\right)$
$tr\left(\mathbf{XY}\right)=tr\left(\mathbf{YX}\right)$
$tr\left({\mathbf{A}}^T\left(\mathbf{B}\odot \mathbf{C}\right)\right)=tr\left({\left(\mathbf{A}\odot \mathbf{B}\right)}^T\mathbf{C}\right)$

求导例子：
$f=tr\left({\mathbf{Y}}^T\mathbf{MY}\right),\mathbf{Y}=\sigma \left(\mathbf{WX}\right)$
$$\mathrm{d}\mathrm{f}=\mathrm{tr}\left(\mathrm{d}{\mathbf{Y}}^{\mathrm{T}}\mathbf{MY}+{\mathbf{Y}}^{\mathrm{T}}\mathbf{M}\mathrm{d}\mathbf{Y}\right)\Rightarrow \frac{\partial \mathrm{f}}{\partial \mathbf{Y}}=\mathbf{MY}+{\mathbf{M}}^{\mathrm{T}}\mathbf{Y}$$
$$\mathrm{d}\mathbf{Y}=\mathrm{tr}\left({\sigma }^{\prime }\left(\mathbf{WX}\right)\odot \left(\mathbf{W}\mathrm{d}\mathbf{X}\right)\right)$$
$$\mathrm{d}\mathrm{f}=\mathrm{tr}\left({\frac{\partial \mathrm{f}}{\partial \mathbf{Y}}}^{\mathrm{T}}\mathbf{dY}\right)=\mathrm{tr}\left({\frac{\partial \mathrm{f}}{\partial \mathbf{Y}}}^{\mathrm{T}}{\sigma }^{\prime }\left(\mathbf{WX}\right)\odot \left(\mathbf{W}\mathrm{d}\mathbf{X}\right)\right)=\mathrm{tr}\left({\left(\frac{\partial \mathrm{f}}{\partial \mathbf{Y}}\odot {\sigma }^{\prime }\left(\mathbf{WX}\right)\right)}^{\mathrm{T}}\left(\mathbf{W}\mathrm{d}\mathbf{X}\right)\right)$$
于是
$$\frac{\partial f}{\partial \mathbf{X}}={\mathbf{W}}^T\left(\left(\mathbf{MY}+{\mathbf{M}}^T\mathbf{Y}\right)\odot {\sigma }^{\prime }\left(\mathbf{WX}\right)\right)$$

参考：
https://zhuanlan.zhihu.com/p/24709748
https://en.wikipedia.org/wiki/Matrix_calculus#convert_differential_derivative