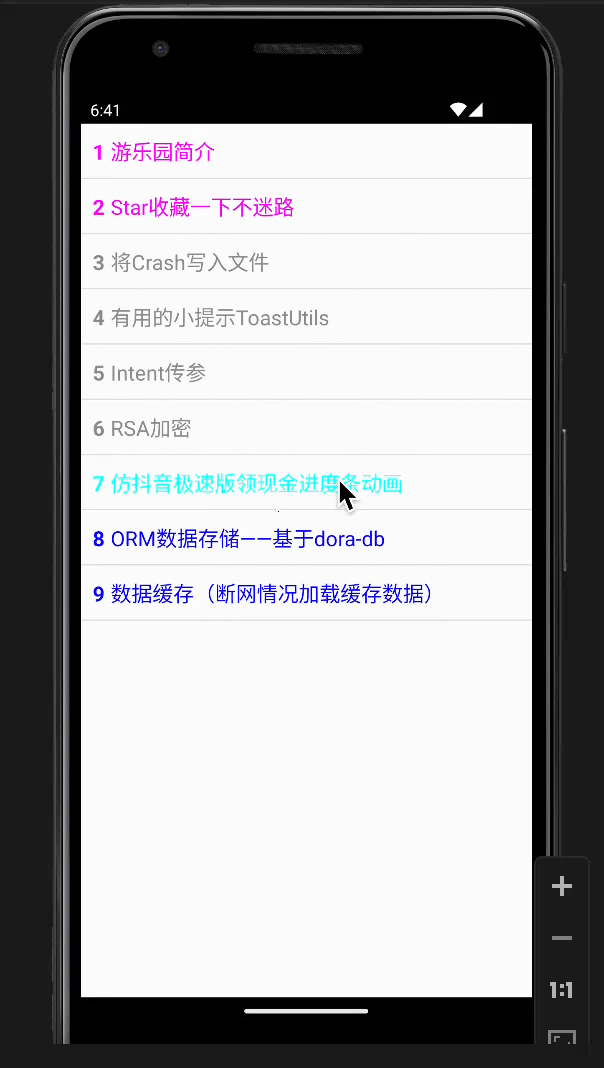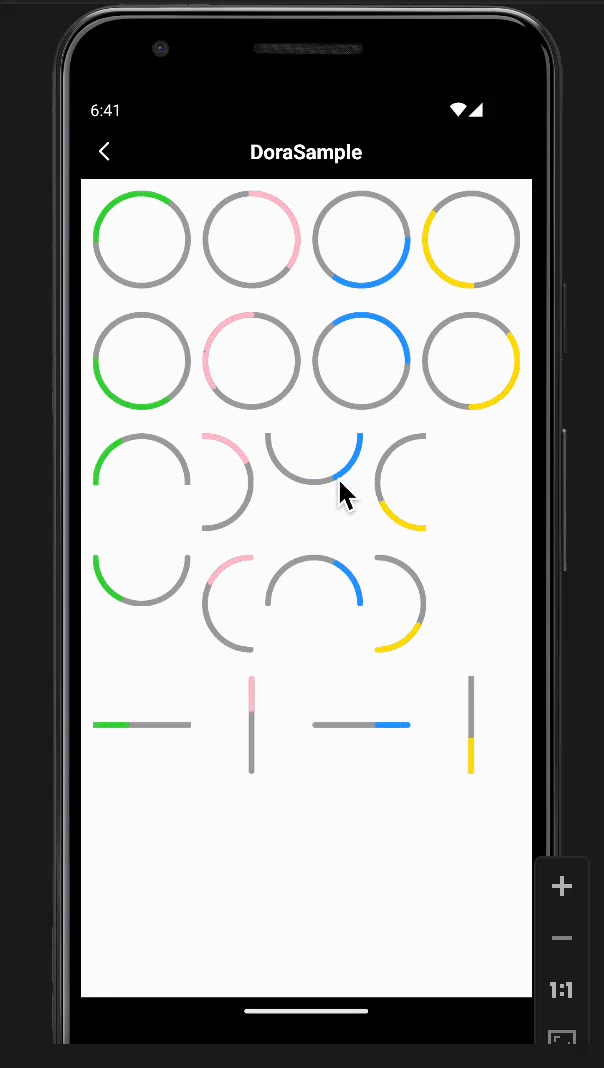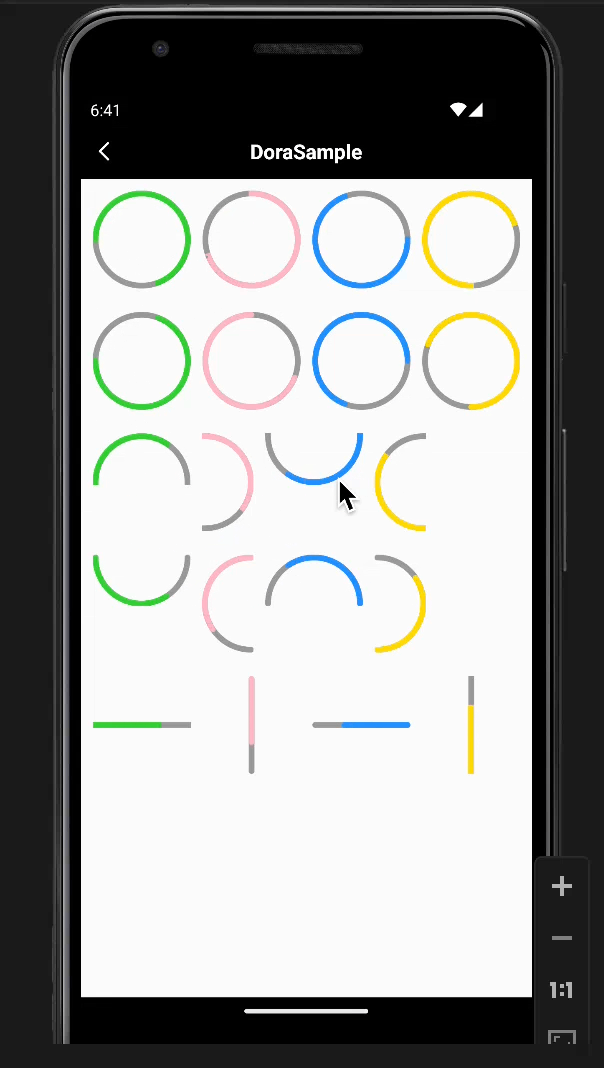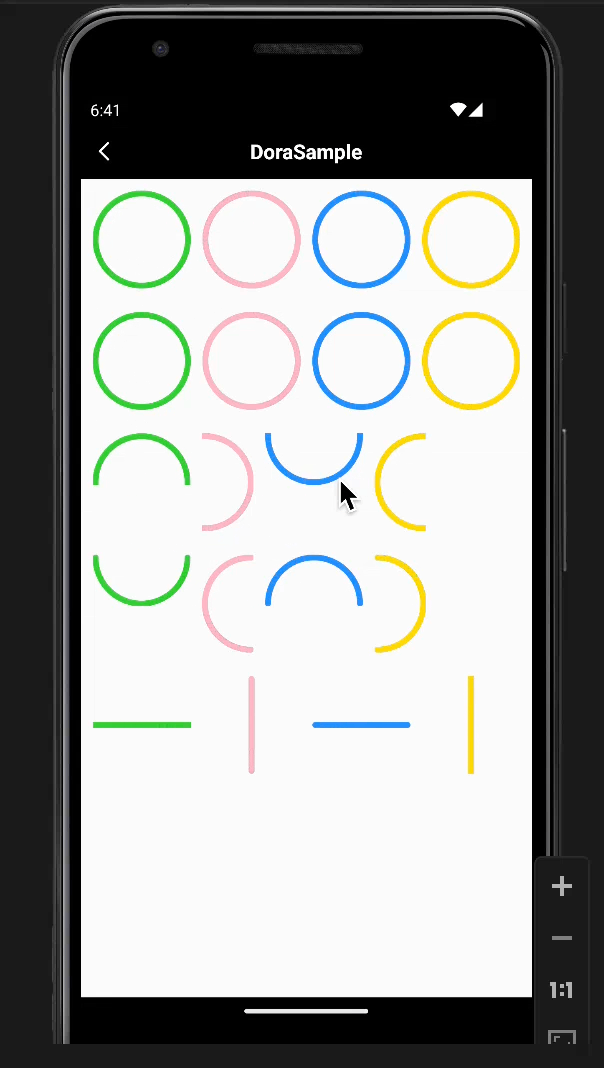
爬楼梯这个题我断断续续看了不下5遍，哪次看都是懵逼的，就会说是满足动态规划，满足斐波那契数列，也不说为什么。

本文一定让你明白怎么分析这个题的规律（利用数学的递推思想来分析），看不懂来打我，但是一定要自己动手画一画台阶写一下。

注意：不论是多少个台阶，第一步就只有两种情况是吧：1步跨1个 or 1步跨2个

思路分析（从最后1个台阶倒着分析）：

1.在最后1个台阶1种跨法：

2.最后2个台阶有2种跨法：

3.最后3个台阶有3种跨法：

4.最后4个台阶有5种跨法：

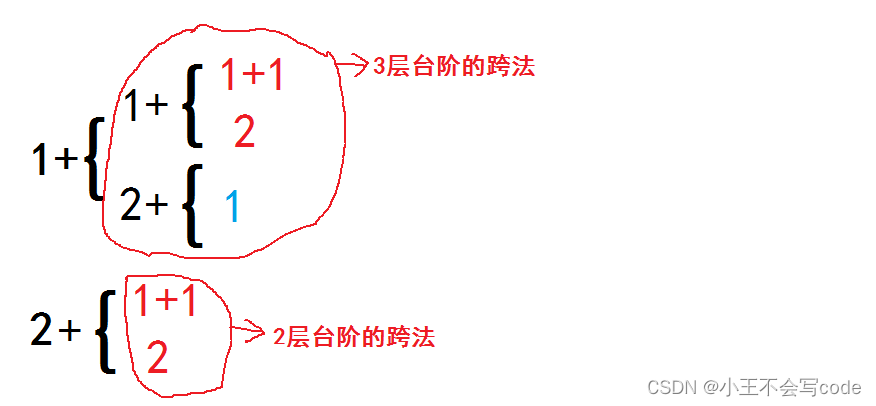
注意：上面几个图里面最左边的数字只表示第一步  跨1个台阶 or 1步跨2个台阶（不懂了看下面这个图）

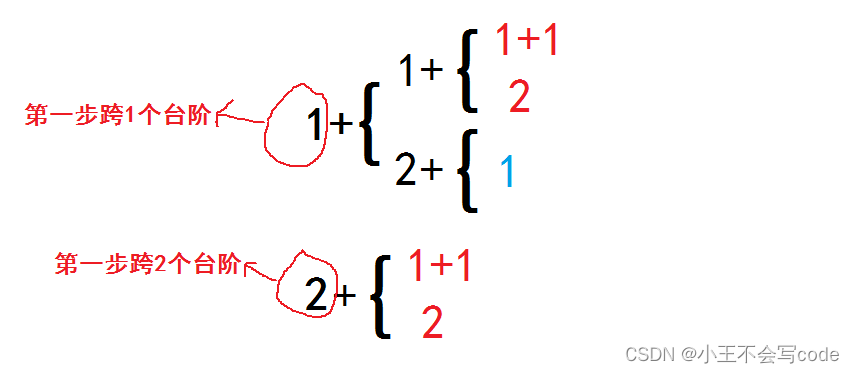
分析最后3个台阶：第一步要么跨1个台阶要么跨2个台阶。当先跨1个台阶时是不是剩下（3-1）个台阶（把跨最后2个台阶的跨法搬过来就行了）；当先跨2个台阶时是不是剩下（3-2）个台阶（把跨最后1个台阶的跨法搬过来就行了）；

分析最后4个台阶：第一步要么跨1个台阶要么跨2个台阶。当先跨1个台阶时是不是剩下（4-1）个台阶（把跨最后3个台阶的跨法搬过来就行了）；当先跨2个台阶时是不是剩下（4-2）个台阶（把跨最后2个台阶的跨法搬过来就行了）；

分析最后5个台阶：第一步要么跨1个台阶要么跨2个台阶。当先跨1个台阶时是不是剩下（5-1）个台阶（把跨最后4个台阶的跨法搬过来就行了）；当先跨2个台阶时是不是剩下（5-2）个台阶（把跨最后3个台阶的跨法搬过来就行了）；

根据数学递推思想可以看出：最后n个台阶的跨法=（n-1）个台阶的跨法+（n-2）个台阶的跨法

既然分析出来与符合斐波那契数列规律是一样的，不妨拿过来斐波那契数列的代码就行了

class Solution {
    public int climbStairs(int n) {
if (n <= 1) return n; // 因为下面直接对dp[2]操作了，防止空指针
        int[]dp=new int[n+1];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) { // 注意i是从3开始的
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}