新材料
直接模拟:因为要考虑上次出现的位置,所以使用map映射最好,如果没有出现过就建立新映射,如果出现过但是已经反应过就跳过,如果出现过但是不足以反应,就建立新映射,如果能反应就反应,并标记。
#include <bits/stdc++.h>
using namespace std;
map<int,int>mp;
int n,k;
int main(){
scanf("%d%d",&n,&k);
int ans=0;
for(int i=1;i<=n;i++){
int cur;scanf("%d",&cur);
if(!mp.count(cur))mp[cur]=i;//有返回1无返回0,返回-1表示已经反应过了
else if(mp[cur]==-1)continue;
else if(i-mp[cur]>k)mp[cur]=i;
else ans^=cur,mp[cur]=-1;
}
cout<<ans<<'\n';
}星际航行


我们的任务是把三维的一群点,变成任意两维都相同,另一维是个差为1的等差数列,然后求最小代价。其实我们可以枚举下哪两维相同,然后计算代价,再计算剩下的一维变成等差数列的代价。
任务1:把一个维度上的所有点变到同一个位置的最小代价就是把所有点都挪到中间点上,你可以画图证明:每两个点之间挪动的代价恰好都是两点之间的线段距离的情况下,总代价最小。
如图:我们只要保证更多的点分布在中间点的两边,且两边的点都恰好连成线段时候代价是最小的(这个偶数的点的情况,奇数的点的情况会更加明显)
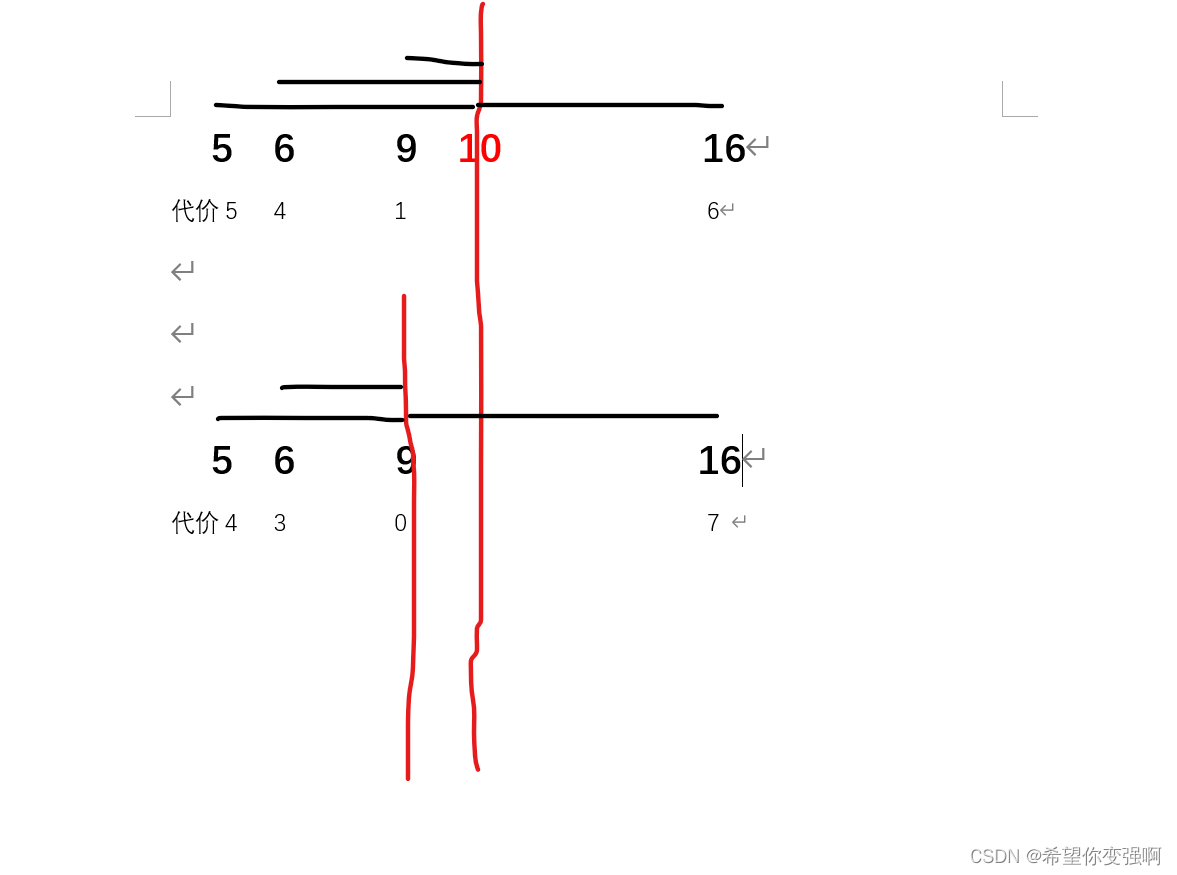
(上面的的是选10为中间点,下面的是选9为中间点)
任务2:要把一个维度上所有点变成一个等差数列且代价最小,就必须不能改变它们之间原来的顺序。如图:(我们假设最终的点的起点是t,那么所有点最终坐标是t+i)

那么最终的代价是sum|xi-(t+i)|最小,然后我们再变形一下:sum|(xi-i)-t|,诶,这不就是所有点xi-i到t的代价最小吗,我们只需要在重复一下上面任务1的做法就行了。
那么最终做法就是:先把数组排序,然后找到求每个点到中间的点的距离和,最终求出两个度的代价,然后在求ai=ai-i,再做一遍,这样就枚举出了一种情况了,然后把所有情况都枚举一下就行了。