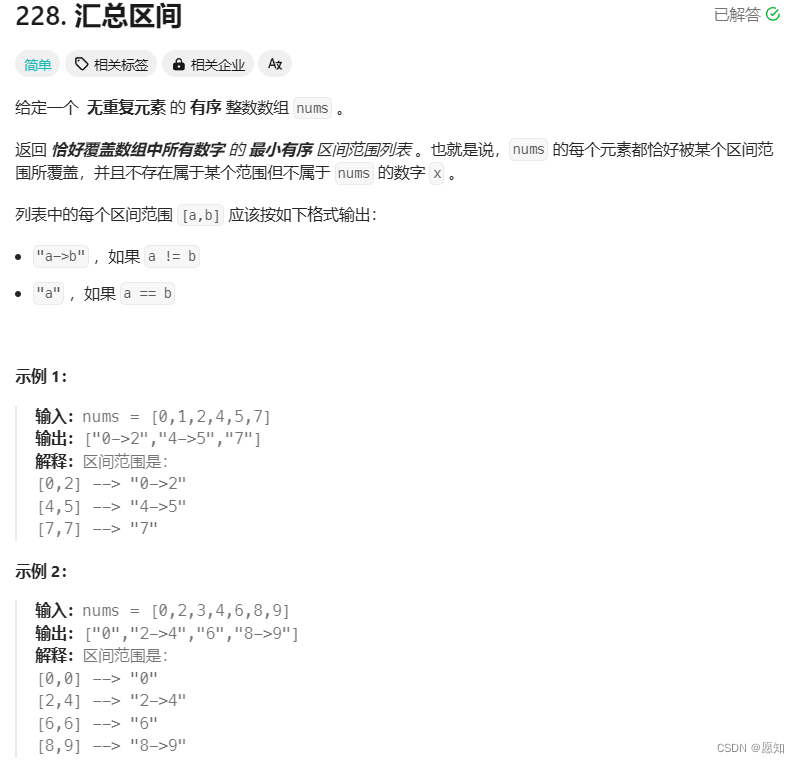
题目一：

代码如下：

vector<string> summaryRanges(vector<int>& nums)
{
	vector<string> ret;
	if (nums.size() == 0)
		return ret;
	int n = nums.size();
	int i = 0;
	while (i < n)
	{
		int prev = i;
		++i;
		while (i < n && nums[i] == nums[i - 1] + 1)
			++i;
		int cur = i - 1;
		string tmp = to_string(nums[prev]);
		if (prev < cur)
		{
			tmp += "->";
			tmp += to_string(nums[cur]);
		}
		ret.push_back(tmp);
	}
	return ret;
}

思路整理：其实是将连续的元素进行合并，单独的元素自己成为一个区间即可。

具体逻辑以及变量解释：

<1>结合序列有序的性质，i遍历整个序列，prev指向连续区间的左端点，cur指向连续区间的右端点。

<2>当nums[i] - nums[i - 1] == 1时，说明区间连续递增，此时i向后移动。

<3>否则说明找到连续递增区间的右区间的下一个位置，此时cur应该为 i - 1，再通过判断左右端点是否重合来判定区间中元素个数。从而确定是否要添加特定符号即可，再将结果存入ret中，最后返回ret即可。

题目二：

代码如下：

vector<vector<int>> merge(vector<vector<int>>& intervals)
{
	vector<vector<int>> ret;
	sort(intervals.begin(), intervals.end());

	int i = 0;
	while (i < intervals.size())
	{
		int left = intervals[i][0];
		int right = intervals[i][1];
		int j = i + 1;
		while (j < intervals.size() && intervals[j][0] <= right)
		{
			right = max(right, intervals[j][1]);//取两者右区间较大值
			++j;
		}
		ret.push_back({ left, right });
		i = j;//跳过已经合并的区间
	}
	return ret;
}

思路整理：通过每个部分的第二个元素和后面每个部分的第一个元素对比，如果当前部分的第二个元素比后面部分的第一个元素大，就可以合并。否则就不合并。开始尝试合并新的区间即可。

具体逻辑及变量解释：

<1>首先通过每个部分的第一个元素进行排序（便于合并操作）。

<2>i用来遍历整个序列，left代表每个小部分的第一个元素，right代表每个小部分的第二个元素，j用来在每次合并时进行遍历。

<3>j指向i的下一个，判断intervals[i][1]是否大于等于intervals[j][0]，如果是，那么j后移，直到条件不符合，将合并的区间放入最终返回的结果中。

<4>i = j，跳过已经合并的区间即可。

<5>返回最终结果。

另外，还有一道57题插入区间，其实可以直接插入序列，然后进行排序之后再进行一次区间合并就行，逻辑和这道题是一样的。