文章目录
- 前言
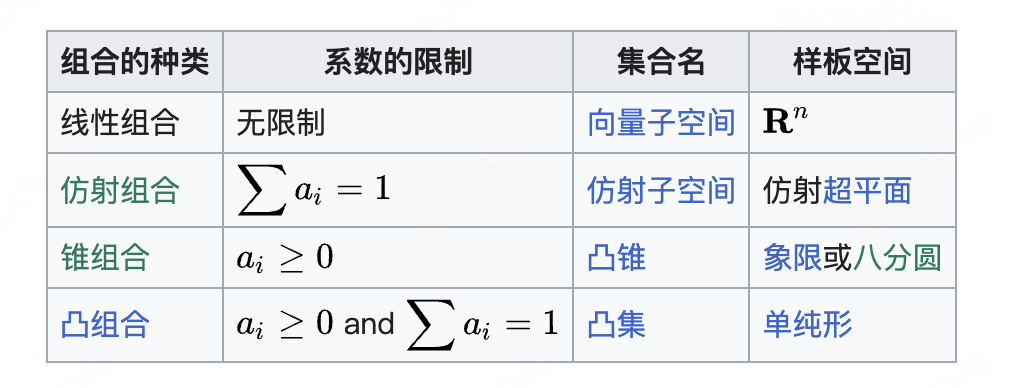
- 组合
- 线性组合 (linear combination)
- 仿射组合 (affine combination)
- 锥组合 (conic combination)
- 凸组合 (convex combination)
- 集合
- 仿射集合
- 凸集合
- 练习:哪个图形是凸的,哪个是仿射的?
- 参考资料
前言
组合侧重于描述由一些基点生成新的点,强调的是不同点的权重和几何位置。
集合侧重于描述许多个点形成的形状,强调的是完整性和连通性。
组合
线性组合 (linear combination)
S
S
S是一向量空间
V
V
V的子集合,如果存在有限多个向量属于
S
S
S,和对应的标量
a
1
,
a
2
,
.
.
.
,
a
n
∈
F
a_1, a_2, ...,a_n \in F
a1,a2,...,an∈F,使得:
v
=
∑
i
=
1
n
a
i
v
i
=
a
1
v
1
+
a
2
v
2
+
.
.
.
+
a
n
v
n
v =\sum_{i=1}^{n}a_iv_i= a_1v_1+a_2v_2+...+a_nv_n
v=i=1∑naivi=a1v1+a2v2+...+anvn
我们称
v
v
v是
(
v
1
,
.
.
.
,
v
n
)
(v_1,..., v_n)
(v1,...,vn)的线性组合。
在二维空间里,如果对 α n \alpha_n αn没有任何限制的话, a 1 v 1 + a 2 v 2 + . . . + a n v n a_1v_1+a_2v_2+...+a_nv_n a1v1+a2v2+...+anvn可以扩散出整个空间。
仿射组合 (affine combination)
在上面线性组合的定义中,如果
∑
i
=
1
n
a
i
=
1
\sum_{i=1}^{n}a_i=1
i=1∑nai=1
我们则称
v
v
v是
(
v
1
,
.
.
.
,
v
n
)
(v_1,..., v_n)
(v1,...,vn)的仿射组合。
在二维空间里,仿射组合可以看作一条经过两个点的直线(两端可以无限延伸)。
锥组合 (conic combination)
在上面线性组合的定义中,如果
a
i
≥
1
a_i \geq 1
ai≥1
我们则称
v
v
v是
(
v
1
,
.
.
.
,
v
n
)
(v_1,..., v_n)
(v1,...,vn)的锥组合。像个冰淇淋🍦一样。
在二维空间里,可以想象是从一条原点出发的射线区域。
凸组合 (convex combination)
在上面线性组合的定义中,如果
a
i
≥
1
,且
∑
i
=
1
n
a
i
=
1
a_i \geq 1,且 \sum_{i=1}^{n}a_i=1
ai≥1,且i=1∑nai=1
我们则称
v
v
v是
(
v
1
,
.
.
.
,
v
n
)
(v_1,..., v_n)
(v1,...,vn)的凸组合,可以看到凸组合的要求是最严格的,相当于是锥组合和仿射组合的交集。
在二维空间里,凸组合可以看作一条经过两个点的线段。
集合
仿射集合
仿射集合里任意两点的连线仍然在集合里。
凸集合
凸集合里任意两点的线段都在集合里。比如一个圆形,就是一个凸集合,但它不是一个放射集合。
练习:哪个图形是凸的,哪个是仿射的?
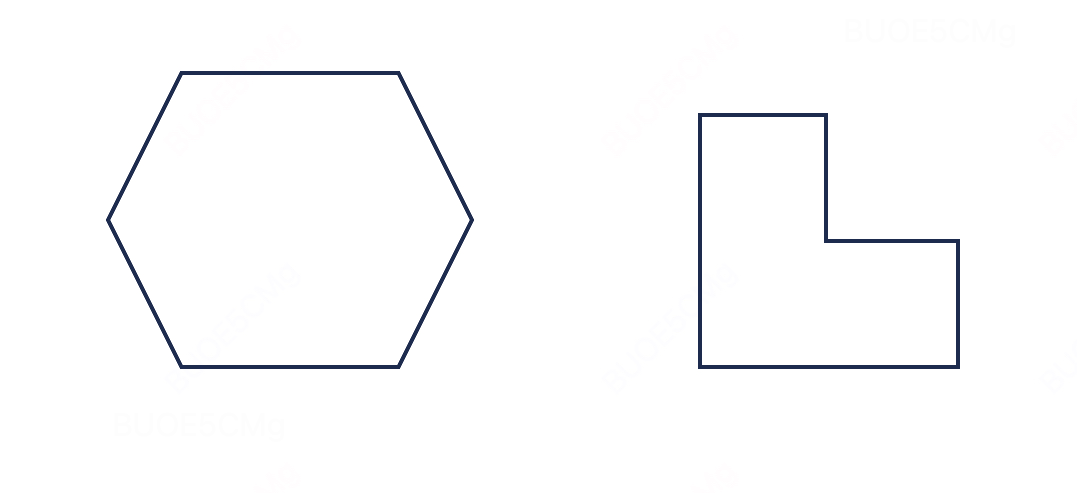
下面两幅图,哪个是凸的,哪个是仿射的?
- 左图:凸的,但不是仿射的;
- 右图:不是凸的,也不是仿射的。
参考资料
- 线性规划 方述诚
- 线性组合


![[论文笔记]MemGPT: Towards LLMs as Operating Systems](https://img-blog.csdnimg.cn/img_convert/84605a0fb8d658bf3fa37cfa04eafd25.png)