目前国内外对于小波分析在降噪方面的方法研究中，主要有小波分解与重构法降噪、小波阈值降噪、小波变换模极大值法降噪等三类方法。

(1)小波分解与重构法降噪

早在1988 年，Mallat提出了多分辨率分析的概念，利用小波分析的多分辨率特性进行分解。小波分解能将含噪信号分解，得到一组小波系数，然后在重构时对噪声所在频带小波系数进行舍弃，从而有效的进行信号的降噪。其文章中也给出了小波分解和重构的快速算法，称为 Mallet 算法。小波分解与重构法降噪是小波分析被应用于降噪领域最为基本的方法，也是后续一些降噪方法的基础。

(2)小波阈值降噪

小波阈值降噪的基本原理是将混合信号进行不同层次的小波分解，在每个层次利用阈值对小波系数进行处理，过滤掉噪声所在频带，然后对信号进行重构，达到降噪的目的。噪声信号一般在高频部分，所以一般对每层的高频系数进行阈值处理。

（3）小波变换模极大值降噪方法

在信号领域，信号的重要信息往往包含在其突变部分和奇异点之中，所以对于信号奇异点的检测研究至关重要。在小波变换的理论中，lip指数直接影响着模极大值和分解尺度之间的关系。通常情况下，若lip指数大于零，则该信号的模极大值随着分解尺度的增大而增大；若lip指数小于零，则该信号的模极大值随着分解分解尺度的增大而减小。通常的实测信号之中，有用信号的lip指数大于零，而噪声的lip指数小于零，这样就能对有用信号和噪声进行区分，在选出有用信号产生的模极大值点之后，利用这些有用的模极大值点对信号进行重建，就可以达到降噪的目的。

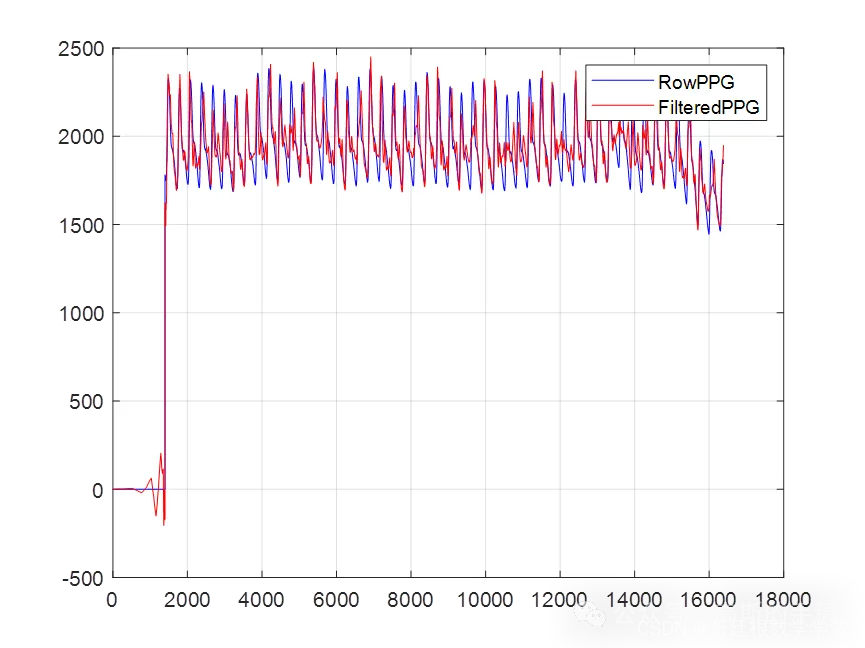
鉴于此，提出一种改进小波降噪方法，该方法提供了一种分解层数选择策略，并使用一个新公式来估计噪声阈值，运行环境为MATLAB R2021B。

%---------------------通过计算peak-to-sum ratio来确定分解层数----------------
%变量初始化
Sj = [1:14]; %每层的peak-to-sum值
Tr = 0.5; %稀疏性判定指标，可调超参数
k = 0; %分解层数

%循环遍历所有的细节系数
for level = 1 : 1 : 14
    %分解到第j层时的细节系数向量
    wj = cell2mat(cD(level)); 
    
    %分为L(负数)与H(正数)两组
    wj_L = []; %负系数数组
    wj_H = []; %正系数数组
    for index = 1 : 1 : length(wj)
        if wj(index) <= 0
            wj_L = cat(1, wj_L, wj(index));
        else
            wj_H = cat(1, wj_H, wj(index));
        end
    end

    %分别用元胞数组记录
    cD_L{level, 1} = wj_L; 
    cD_H{level, 1} = wj_H; 

    %计算peak-to-sum值，裁定第j的稀疏性
    maxwj = max(abs(wj)); %第j层最大的细节系数
    sumwj = sum(abs(wj)); %第j层细节系数绝对值之和
    Sj(level) = maxwj / sumwj;
    完整代码：https://mbd.pub/o/bread/mbd-ZpWWm59w

end