论文标题:Probabilistic Volumetric Fusion for Dense Monocular SLAM
论文链接:https://arxiv.org/pdf/2210.01276.pdf
论文思想
提出了一种新的方法,通过利用深度密集的单眼SLAM和快速不确定性传播,从图像中重建三维场景
所提出的方法能够密集、准确和实时地对场景进行三维重建,同时对来自密集单眼SLAM的极度嘈杂的深度估计具有鲁棒性
与之前的方法不同的是,这些方法要么使用临时的深度过滤器,要么从RGB-D相机的传感器模型中估计深度的不确定性
概率深度不确定性直接来自SLAM中底层束调整问题的信息矩阵
由此产生的深度不确定性为体积融合的深度图提供了一个极好的信号
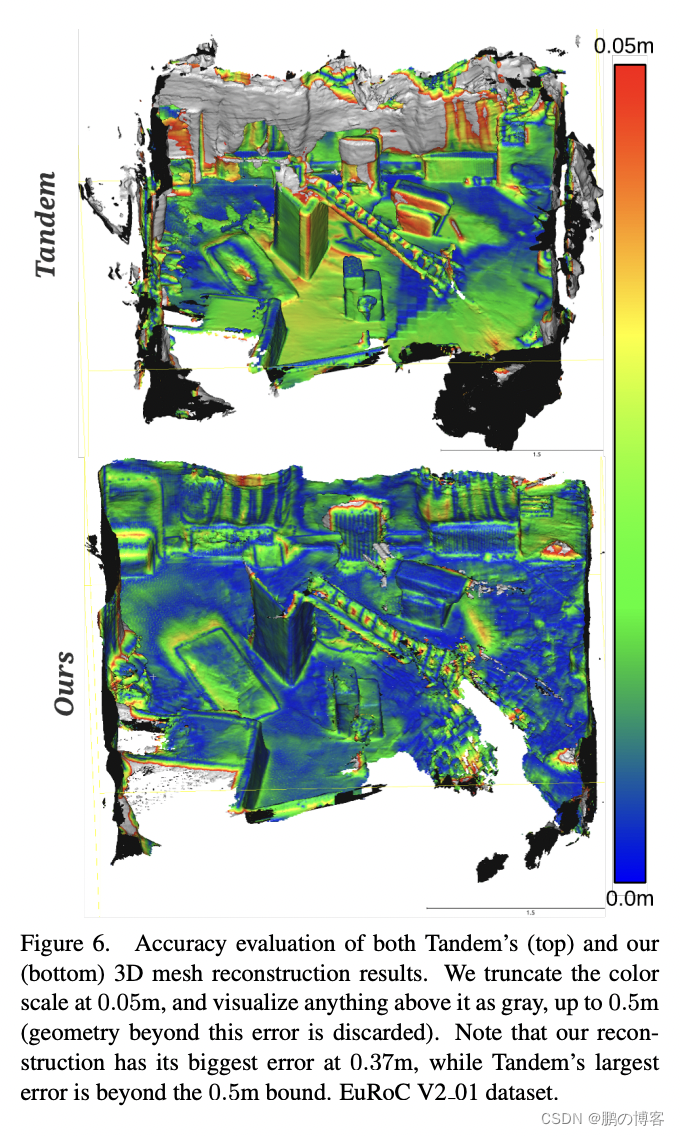
如果没有我们的深度不确定性,产生的网格是有噪音的,而且有人工痕迹,而该方法产生了一个准确的三维网格,人工痕迹明显减少
该方法在具有挑战性的Euroc数据集上提供了结果
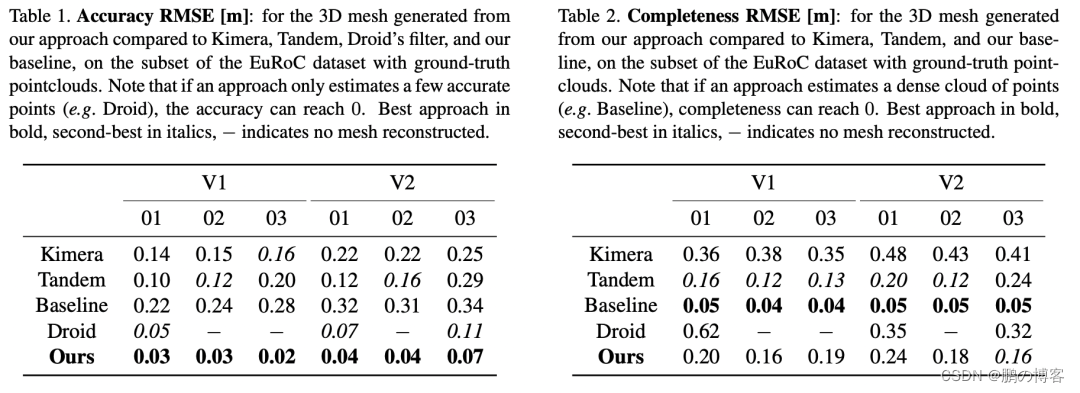
并表明该方法比直接融合单眼SLAM的深度要好92%,与最好的竞争方法相比,精确度提高了90%
论文主要贡献
展示了一种以密集SLAM中的信息矩阵得出的不确定性为权重的密集深度图的体积融合方法
能够在给定的可容忍不确定性的最大水平上重建场景
与其他竞争性方法相比,该方法可以更高的精度重建场景,同时实时运行,并且只使用单眼图像
在具有挑战性的EuRoC数据集中实现了最先进的三维重建性能
主要方法
主要思想是将极其密集但有噪声的深度图通过其概率不确定性加权后融合到一个体积图中
然后提取一个具有给定最大不确定性约束的三维网格
为了实现这一目标,我们利用Droid-SLAM的配方来产生姿势估计和密集的深度图,并将其扩展到产生密集的不确定性图
我们将首先展示我们如何从底层束调整问题的信息矩阵中有效地计算深度不确定性
然后,我们介绍我们的融合策略,以产生一个概率上合理的体积图
最后,我们将展示我们如何在一个给定的最大不确定性约束下从体积中提取一个网状物
论文核心
论文有如下几个核心:
- 密集单眼SLAM
- 逆向深度不确定度估算
- 深度上采样与不确定性传播
- 不确定性的体素建图
- 带有不确定性界限的网格划分
1. 密集单眼SLAM
经典的基于视觉的反深度间接SLAM的核心是解决一个捆绑调整(BA)问题
其中三维几何被参数化为每个关键帧的一组(反)深度
这种结构的参数化导致了解决密集BA问题的一种极其有效的方式
它可以被分解成熟悉的箭头状块状稀疏矩阵,摄像机和深度依次排列
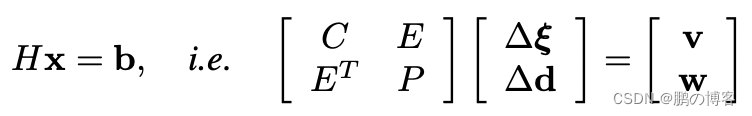
其中H是Hessian矩阵,C是块状摄像机矩阵,P是对应于点的对角线矩阵(每个关键帧每个像素一个反深度)
我们用∆ξ表示SE(3)中相机姿态的谎言代数的delta更新,而∆d是对每像素反深度的delta更新
为了解决BA问题,首先要计算Hessian H相对于P的Schur补数(表示为H/P),以消除反深度变量
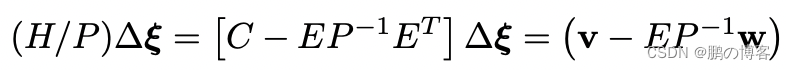
得到的矩阵(H/P)被称为缩小的摄像机矩阵
上述公式中的方程组只取决于关键帧的位置
因此,我们首先使用(H/P)=LLT的Cholesky分解来解决姿势问题, 使用前置和后置替代
然后用得到的姿势解∆ξ来反求逆深度图∆d
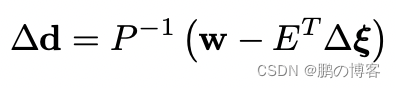
2. 逆向深度不确定度估算
鉴于Hessian的稀疏模式,我们可以有效地提取每个像素深度变量所需的边际协方差。逆深度图Σd的边际协方差为:
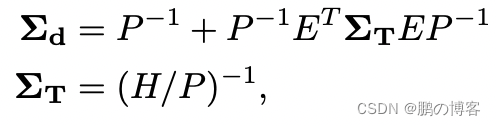
其中ΣT是姿势的边际协方差
不幸的是,H/P的完全反转计算起来很费劲
尽管如此,由于我们已经通过将H/P分解成Cholesky因子解决了原始的BA问题,我们可以通过以下方式重新使用它们
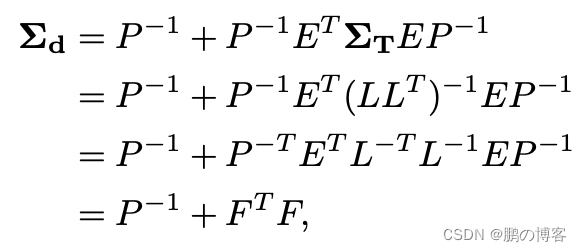
其中:
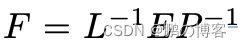
因此,我们只需要反转下三角的Cholesky因子L,这是一个通过代入计算的快速操作
我们可以有效地计算所有的逆矩阵
P的逆是由每个对角线项的元素反转得到的
我们通过反转其Cholesky因子来避免对(H/P)进行完全反转
然后,只需将矩阵相乘和相加即可
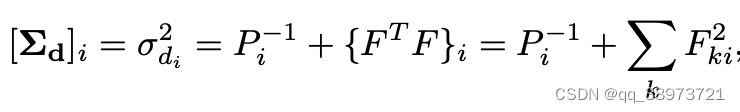
3. 深度上采样与不确定性传播
最后,由于我们希望有一个与原始图像相同分辨率的深度图
我们使用Raft中定义的并在Droid中使用的凸上采样运算对低分辨率深度图进行上采样
这种上采样操作通过对低分辨率深度图中相邻的深度值进行凸组合
为高分辨率深度图中的每个像素计算深度估计值。得到的深度估计值对每个像素来说都是通过以下方式给出的
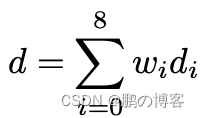
其中wi是学习到的权重(更多细节可以在Raft中找到)
di是我们要计算深度的像素周围的低分辨率反深度图中一个像素的反深度(用一个3×3的窗口来采样相邻的深度值)
假设逆向深度估计之间是独立的,由此产生的逆向深度方差由以下公式给出:
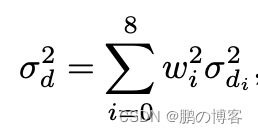
其中wi是公式中用于反深度加样的相同权重,σ 是要计算的像素周围的低分辨率反深度图中一个像素的反深度的方差
我们对反深度和不确定度进行了8倍的放大,从69×44的分辨率到512×384的分辨率
到目前为止,我们一直在处理逆向深度,最后一步是将它们转换为实际深度和深度变异
我们可以通过使用非线性不确定性传播轻松地计算出深度方差
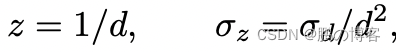

4. 不确定性的体素建图
鉴于每个关键帧都有密集的深度图,因此有可能建立一个密集的场景三维网格
不幸的是,由于其密度,深度图是非常嘈杂的,因为即使是没有纹理的区域也会被赋予一个深度值
体积上融合这些深度图可以减少噪音
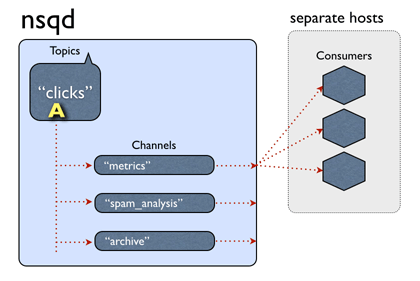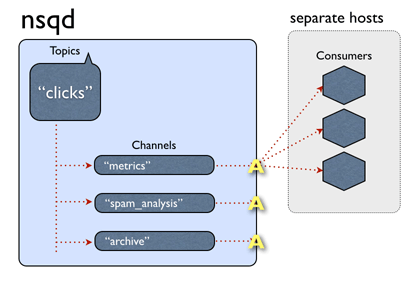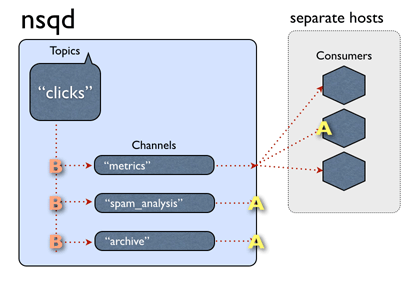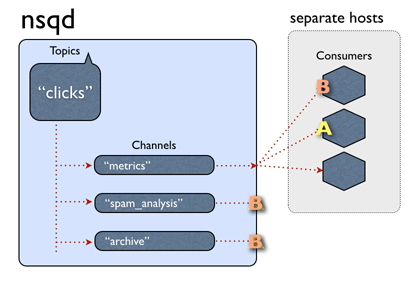
但重建仍然不准确,并受到人工制品的破坏(见图4中的"基线",它是通过融合图1中的点云计算出来的)
虽然可以在深度图上手动设置过滤器
而且Droid实现了一个临时的深度过滤器
但我们建议使用估计的深度图的不确定性,这为重建场景提供了一个强大的、数学上合理的方法
体积融合以概率模型为基础,每个深度测量被假定为独立和高斯分布
在这种表述下,我们试图估计的带符号的距离函数(SDF)φ最大限度地满足以下可能性

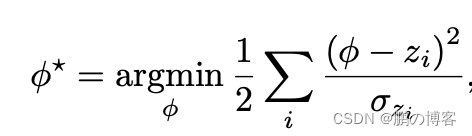
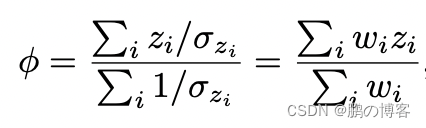
在实践中,对于每一个新的深度图,加权平均数都是增量计算的
通过更新体积中的体素,用一个运行平均数,导致熟悉的体素重建方程式
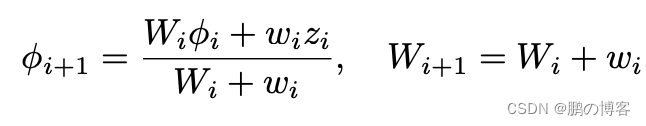
其中Wi是存储在每个体素中的权重
权重初始化为零,W0=0,TSDF初始化为截断距离τ,φ0=τ(在我们的实验中,τ=0.1m)
上述表述作为一个运行中的加权平均,在使用的权重函数方面非常灵活
这种灵活性导致了许多不同的融合深度图的方法,有时会偏离其概率性的表述
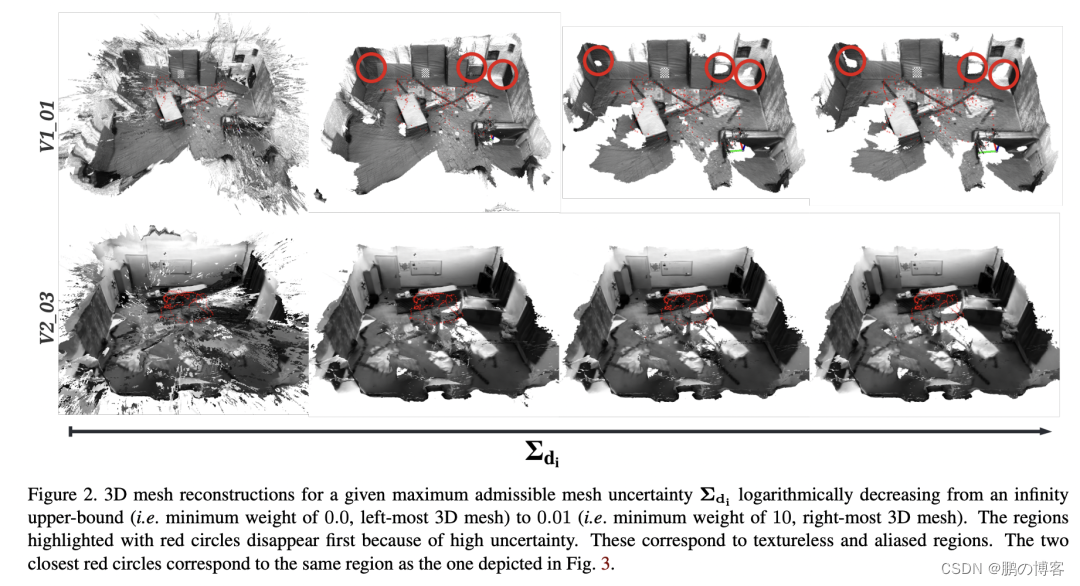
5. 带有不确定性界限的网格划分
鉴于我们的体素对有符号的距离函数有一个概率上合理的不确定性估计
我们可以提取不同水平的允许最大不确定性的等值面
我们使用行进立方体来提取表面,只对那些不确定性估计值低于最大允许不确定性的体素进行网格划分
由此产生的网格只有具有给定的不确定性上限的几何体,而我们的体积包含所有的深度图信息
如果我们将不确定性边界设置为无穷大,即权重为0,我们就会恢复基线解决方案,这是极其嘈杂的
通过逐步减少约束,我们可以在拥有更准确但不完整的三维网格之间取得平衡,反之亦然
在实验中,我们没有试图为我们的方法找到一个特定的帕累托最优解
而是使用了一个固定的不确定度的最大上限0.1
这导致了非常精确的三维网格,但在完整性上有轻微的损失
请注意,如果不固定比例,这个不确定性约束是无单位的,可能需要根据估计的比例来调整
实验