目录
为什么需要关心因果关系?
回答不同类型的问题
当关联确实是因果时
为什么需要关心因果关系?
首先,您可能想知道:它对我有什么好处?下面的文字就将围绕“它”展开:
回答不同类型的问题
机器学习目前非常擅长回答的问题类型是预测类型。正如 Ajay Agrawal、Joshua Gans 和 Avi Goldfarb 在《预测机器》一书中所说,“人工智能的新浪潮实际上并没有给我们带来智能,而是智能的一个关键组成部分——预测”。我们可以用机器学习做各种美妙的事情。唯一的要求是我们将问题构建为预测问题。想从英语翻译成葡萄牙语?然后构建一个 ML 模型,在给定英语句子时预测葡萄牙语句子。想识别人脸?然后构建一个 ML 模型,该模型预测图片子部分中是否存在人脸。想造一辆自动驾驶汽车吗?然后构建一个 ML 模型来预测车轮的方向以及当呈现来自汽车周围的图像和传感器时的刹车和油门压力。
然而,ML 并不是万能的。它可以在非常严格的边界下创造奇迹,但如果它使用的数据与模型习惯的数据略有不同,它仍然会失败。再举一个来自 Prediction Machines 的例子,“在许多行业中,低价格与低销量有关。比如在酒店行业,旅游旺季外价格低,需求旺盛、酒店爆满时价格高。鉴于这些数据,一个幼稚的预测可能表明提高价格会导致售出更多房间。”
ML 在这种逆因果关系类型的问题上是出了名的糟糕。这类问题要求我们回答“假设发生”这样的问题,经济学家称之为反事实。假设我目前要求的商品不是这个价格,而是使用另一个价格,会发生什么情况?假设我不采用这种低脂饮食,而是采用低糖饮食,会发生什么?假设您在银行工作,提供信贷,您将必须弄清楚更改客户线会如何改变您的收入。或者,假设您在当地政府工作,您可能会被要求弄清楚如何改善学校教育系统。您是否应该因为数字知识时代告诉您而将平板电脑送给每个孩子?或者你应该建造一个老式的图书馆?
这些问题的核心是我们希望知道答案的因果调查。因果问题渗透到日常问题中,例如弄清楚如何提高销售额,但它们也在我们非常个人和宝贵的困境中发挥重要作用:我是否必须上一所昂贵的学校才能在生活中取得成功(是吗?教育导致收入)?移民是否会降低我找到工作的机会(移民是否会导致失业率上升)?向穷人汇款会降低犯罪率吗?不管你在哪个领域,很可能你已经或将不得不回答某种类型的因果问题。不幸的是,对于 ML,我们不能依靠相关类型预测来解决它们。
回答这类问题比大多数人想象的要困难。您的父母可能已经向您反复说过“关联不是因果关系”,但实际上要解释为什么会这样却是有点困难的。这也是因果关系要讲的。至于其余部分,它将致力于弄清楚如何使关联成为因果关系。
当关联确实是因果时
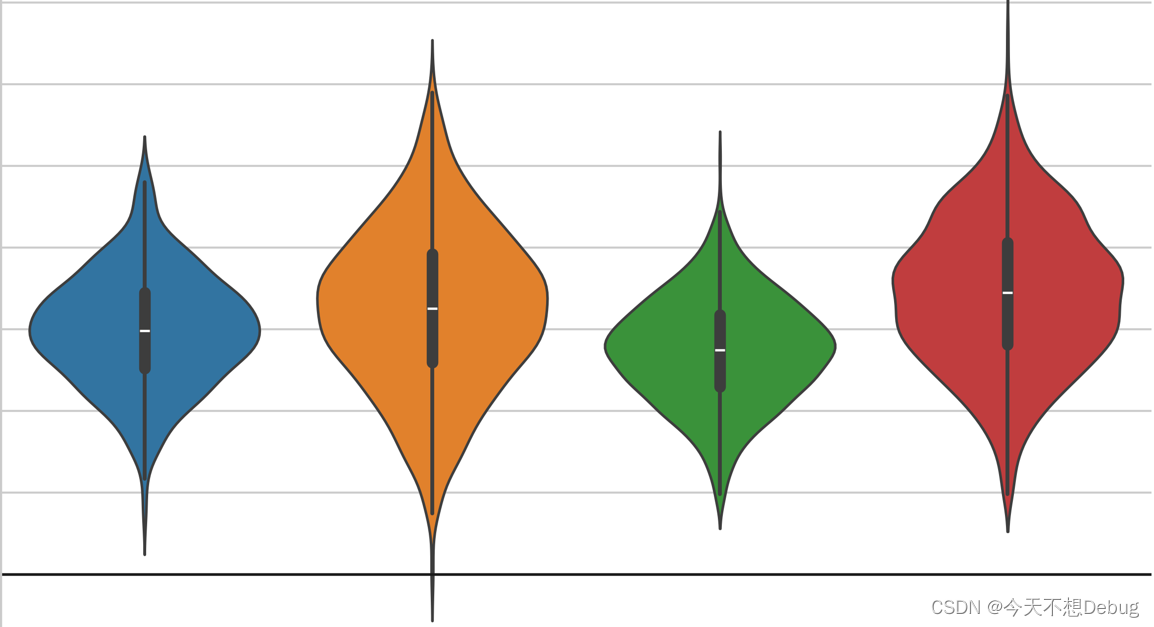
直觉上,我们模糊地知道为什么关联不是因果关系。 如果有人告诉您,为学生提供平板电脑的学校比不提供平板电脑的学校表现更好,您可以很快指出,那些配备平板电脑的学校可能更富有。 因此,即使没有平板电脑,他们的表现也会比平均水平更好。 因此,我们不能得出结论说,在课堂上给孩子们使用平板电脑会提高他们的学习成绩。 我们只能说学校的平板电脑与学习成绩表现好有关。
import pandas as pd
import numpy as np
from scipy.special import expit
import seaborn as sns
from matplotlib import pyplot as plt
from matplotlib import style
style.use("fivethirtyeight")
np.random.seed(123)
n = 100
tuition = np.random.normal(1000, 300, n).round()
tablet = np.random.binomial(1, expit((tuition - tuition.mean()) / tuition.std())).astype(bool)
enem_score = np.random.normal(200 - 50 * tablet + 0.7 * tuition, 200)
enem_score = (enem_score - enem_score.min()) / enem_score.max()
enem_score *= 1000
data = pd.DataFrame(dict(enem_score=enem_score, Tuition=tuition, Tablet=tablet))
plt.figure(figsize=(6,8))
sns.boxplot(y="enem_score", x="Tablet", data=data).set_title('ENEM score by Tablet in Class')
plt.show()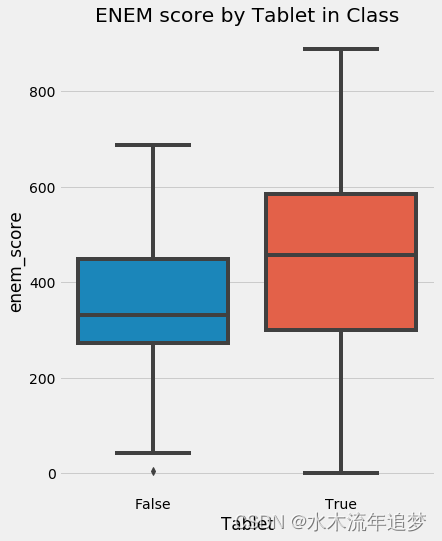
为了超越简单的直觉,让我们首先建立一些符号。 这将是我们谈论因果关系的共同语言。 把它想象成我们将用来识别其他勇敢和真正的因果战士的通用语言,它将在未来的许多战斗中组成我们的呼声。
表示单元i的干预量,
![]()
这里的干预不需要是药物或医学领域的任何东西。 相反,它只是一个术语,我们将用它来表示一些我们想知道其效果的干预。 在我们的案例中,治疗是给学生服用药片。 作为旁注,您有时可能会看到D而不是T来表示干预。然后把称为单元i的观察结果变量。
结果是我们感兴趣的变量。 我们想知道干预是否有任何影响。 在我们的平板电脑示例中,它将是学习成绩。这就是事情变得有趣的地方。 因果推断的基本问题是我们永远无法在经过处理和未经处理的情况下观察到同一个单元。 就好像我们有两条不同的道路,我们只能知道我们走的那条路前面有什么。
为了解决这个问题,我们将在潜在结果方面进行很多讨论。它们被成为潜在的结果是因为它们实际上并没有发生。相反,它们表示在采取某些干预的情况下会发生什么。我们有时将发生的潜在结果称为事实,而将未发生的潜在结果称为反事实。
至于符号,我们使用了一个额外的下标:是未经处理的单元i的潜在结果,
是相同单元i的潜在结果。而有时也表示为
,
可以是
而
可以是
。回到我们的例子,如果学生i拿到平板电脑,我们可以观察到
,否则我们可以观察到
,我们可以定义个体治疗效果:
-
当然,由于因果推断的根本问题,我们永远无法知道个体的治疗效果,因为我们只观察了其中一种潜在结果。目前,让我们关注一些比估计个体治疗效果更容易的事情。相反,让我们关注平均处理效果,其定义:,其中E是期望。另一个更容易估计的数量是对被干预者的平均干预效果:
![]()
现在,我知道我们不能看到两种潜在的结果,但为了争论,我们假设我们可以。假设因果推理之神对我们进行的许多统计斗争感到满意,并以上帝般的力量奖励我们,以查看替代的潜在结果。有了这种能力,假设我们收集了 4 所学校的数据。我们知道他们是否向学生提供平板电脑以及他们在某些年度学术测试中的分数。在这里,平板电脑是治疗方法,所以T=1如果学校向孩子们提供平板电脑,Y将是测试分数。
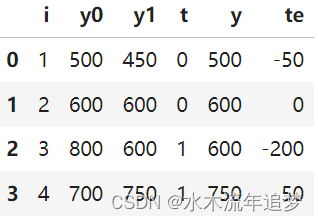
这里的ATE将是最后一列的平均值,即治疗效果的平均值:ATE=(-50+0-200+50)/4 = -50
这意味着平板电脑会使学生的学习成绩平均降低 50 分。 当 T=1 时,这里的ATT将是最后一列的平均值:ATT=(-200+50)/2=-75
也就是说,对于接受治疗的学校,平板电脑使学生的学习成绩平均降低了 75 分。 当然,我们永远无法知道这一点。 实际上,上表如下所示:
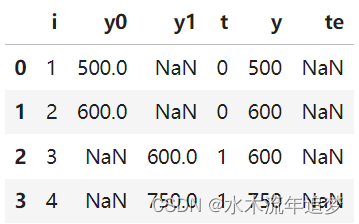
您可能会说,这肯定不理想,但我不能仍然采用处理过的平均值并将其与未处理过的平均值进行比较吗? 换句话说,我不能只做ATE=(600+750)/2-(500+600)/2=125么?不!注意结果的不同。 那是因为你刚刚犯了将联想误认为因果关系的最严重的罪过。 要了解原因,让我们来看看因果推理的主要敌人。