前言

分形理论是一种非常重要的科学概念，它被广泛应用于物理学、数学、生物学等领域。分形理论描述了一种重复自相似的结构，这种结构在不同的尺度上都具有类似的形态。由于分形理论的应用广泛且深远，了解分形理论可以帮助人们更好地理解自然界和人造世界中的现象。

作为一个科学的文化人，了解分形理论可以让我们更深入地理解我们生活中的事物和现象。分形理论帮助我们认识到自然界中的很多形态都是由简单的重复而构成的，这种认识使我们对世界的理解更加深入和全面。此外，分形理论还可以被用于解释复杂系统的行为，为我们提供了一种新的思考和分析问题的方式。

因此，了解分形理论是成为一个科学的文化人的基本要求之一。它帮助我们更好地理解和解释世界，提供了一种新的思考和分析问题的方式。对于科学的研究和文化的发展都是非常重要的。

从欧几里得到分形

从欧几里得几何的两千多年来

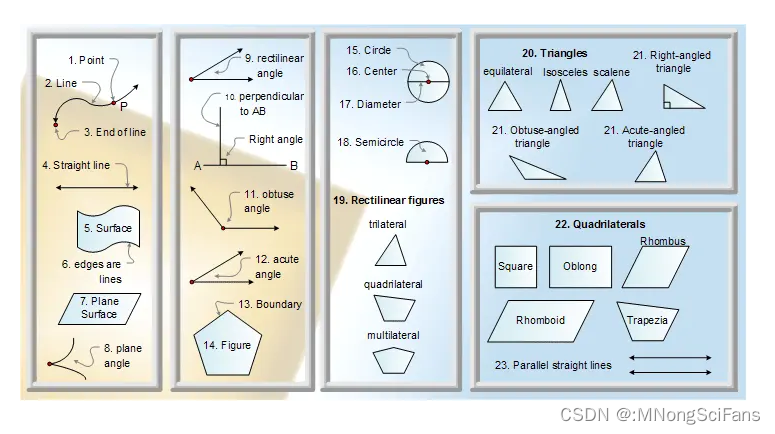
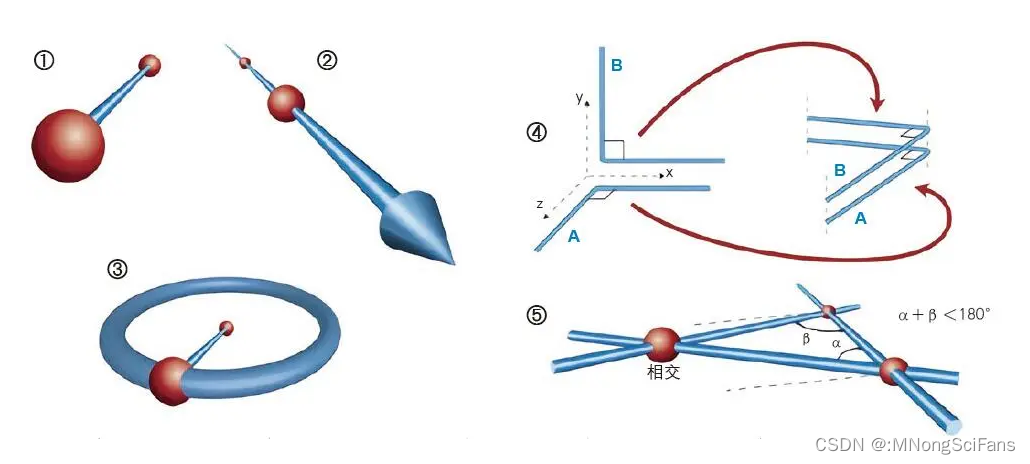
在大自然复杂表面下的内在数学秩序里面，有很多奇奇怪怪的分形结构：Sierpinski  triangle三角形、Weierstrass函数、皮亚诺曲线、Koch雪花。分形提供了新的描述自然的方式。其复杂的背后，隐藏着局部和整体之间“自相似”的本质联系。

虽然许多分形是自相似的 ，但一个更好的定义是，分形是具有非整数维的形状。

比如说，瓦茨拉夫·谢尔宾斯基在1915年提出的Sierpinski三角形、Sierpinski地毯。还有PaulLévy在1938年提出的LévyC曲线。这类重复的或者自身相似的数学图形，1975年，Mandelbrot正式提出了“分形”一词，并用醒目的计算机构建的可视化效果说明了他的数学定义。

利用加斯顿·朱利亚创立迭代理论和公式z = z² + c，通过高性能计算机对数字进行了成千上万次的运算和处理，最终成功绘制出一个上帝的指纹。

曼德布罗特集（Mandelbrot Set）

公式采用变量z和参数c，映射了复平面上的数值。其中x轴测量复数的实数部分，而 y 轴测量复数的虚数部分。

迭代是重复反馈过程的活动，其目的通常是为了逼近所需目标或结果。每一次对过程的重复称为一次“迭代”，而每一次迭代得到的结果会作为下一次迭代的初始值。

在Mandelbrot集中，你会明白分形是一种具有自相似特性的现象、图像或者物理过程。

可以说分形的核心就是自相似性，就是取任一部分进行适当放大，仍可得到与原来整个图形相似的图形，就相当于不断的克隆，一个比一个小，不停的重复下去。

谢尔宾斯基三角形（Sierpinski triangle）

Sierpinski  triangle 是一个由三个等边三角形组成的无限分形结构。它的构造方法是通过将一个等边三角形不断地分割成四个互相相似的小三角形，并去掉中间的那个三角形。这个过程可以无限循环下去，形成一个具有自相似性的图案。

皮亚诺曲线（Peano curve）

1890年，意大利数学家皮亚诺（Peano G）发明能填满一个正方形的曲线，叫做皮亚诺曲线。后来，由希尔伯特作出了这条曲线，又名希尔伯特曲线。Hilbert-Peano曲线是一种分形图形，它可以画得无限复杂。它的初始图元是正方形，在迭代生成的过程中，不断细化出小的正方形，图中的线段其实是用于连接各正方形的连线。它的特点是蜿蜒曲折、一气呵成，能经过平面上某一正方形区域内所有的点。希尔伯特曲线是一种奇妙的曲线，只要恰当选择函数，画出一条连续的参数曲线，当参数t在0，1区间取值时，曲线将遍历单位正方形中所有的点，得到一条充满空间的曲线。 希尔伯特曲线是一条连续而又不可导的曲线。

分形维数表明它比普通线更有效地局部填充空间。

科赫雪花（Koch Snowflake）

科赫雪花是一条分形曲线，也被称为科赫岛，由赫尔格·冯·科赫于 1904 年首次描述。它是通过从一个等边三角形开始构建的，移除每条边的内三分之一，在移除该边的位置构建另一个等边三角形，然后无限期地重复该过程。Koch 雪花可以简单地编码为 Lindenmayer 系统，初始字符串为“F--F--F”，字符串重写规则为“F”->“F+F--F+F”，角度为 60 度。

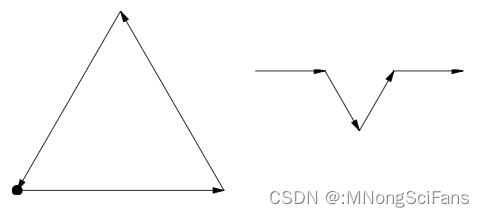
构造的第 0 次到第 3 次迭代。

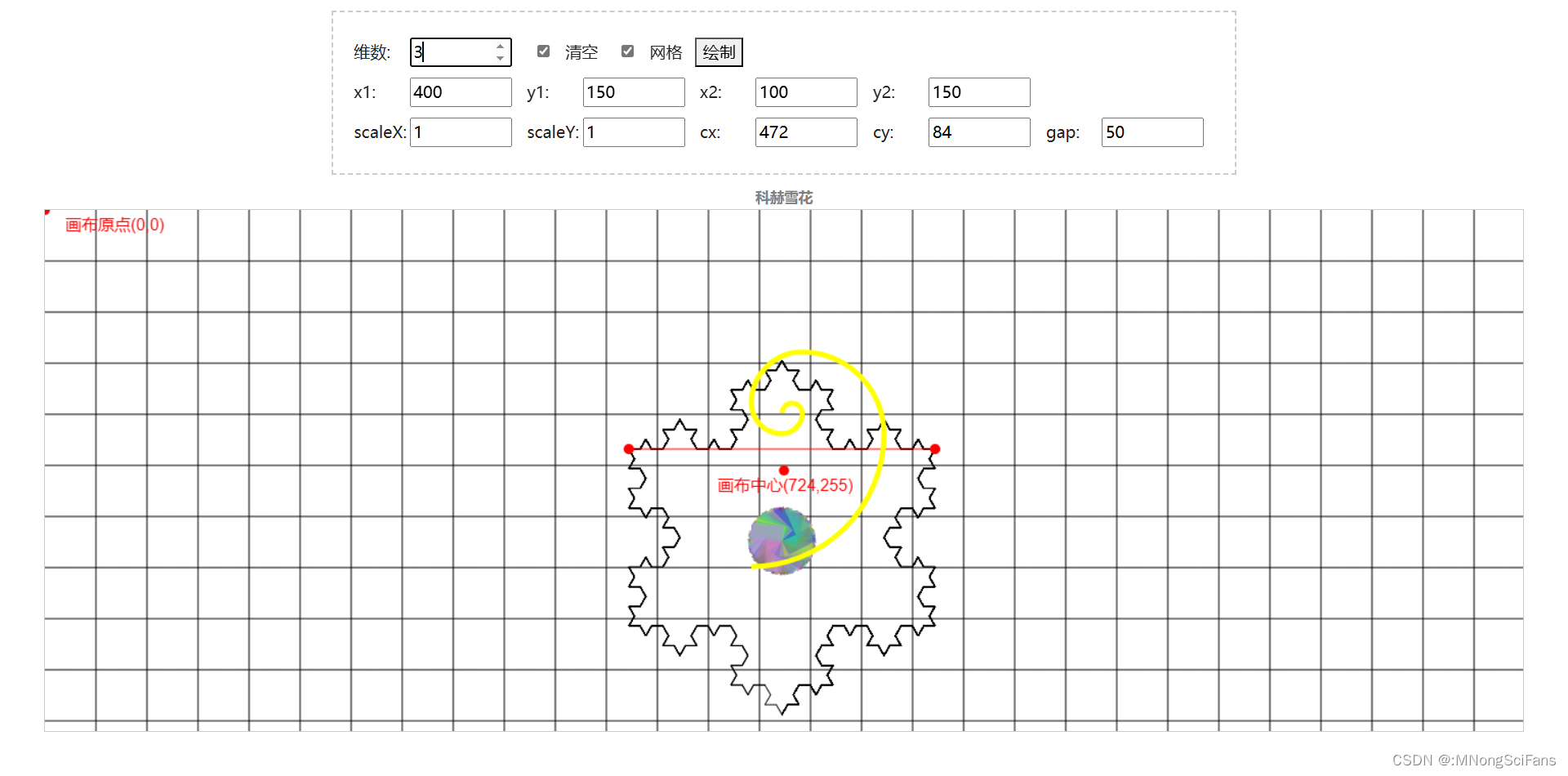
三角形的每个分形边有时被称为科赫曲线。一般而言，我们在测量非分形曲线时，都是将其放大到足够大，再用直线拟合一小段曲线，在一小段范围内取一阶泰勒展开，近似为直线，最后求总长度。但这样的方法，对分形曲线根本行不通。因为你会发现，分形图案是无限迭代的，无论缩放到多小，细节总会不断地出现。

Koch curve 是经典的迭代分形曲线。它是通过迭代缩放起始段而形成的理论构造。每个新段按 1/3 的比例分为 4 个首尾相连的新片段，其中 2 个中间片段在其他两个片段之间相互倾斜，因此如果它们是三角形，其底边就是中间的片段的长度，这样整个新段就适合传统上测量的前一个段端点之间的长度。虽然动画只显示了几次迭代，但理论曲线以这种方式无限缩放。在这么小的图像上超过大约 6 次迭代，细节就会丢失。

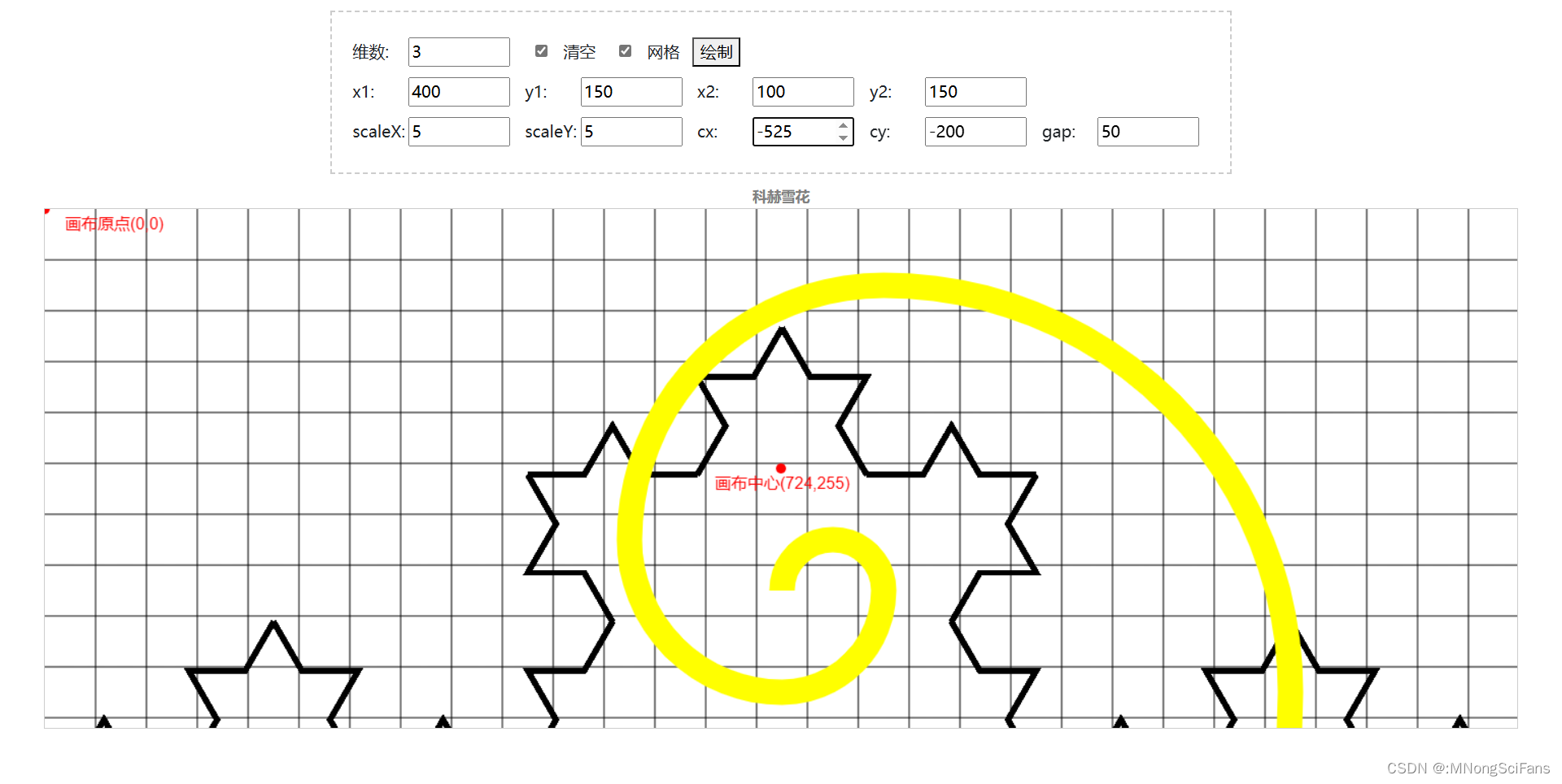
科赫雪花的生长规则是：从一个正三角形出发，把每条边三等分，然后以各边的中间部分1/3的长度为底边，分别向外作正三角形，再把“底边”线段抹掉，得到一个“六角星”。再把每条边三等分，以各中间部分的长度为底边，向外作正三角形后，抹掉底边线段。反复进行这一过程，就会得到一个类似于“雪花”的图形。我们将这种雪花称为“科赫雪花”。

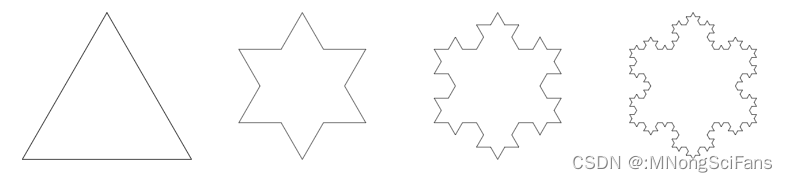
从一个单一的等边三角形开始，但是，我们没有 在每个步骤中去移除 更小的三角形，而是沿边缘 添加 更小的三角形，每个三角形的边长是上一步骤中三角形的1/3。无限生长下去，它将是一个无限大周长，但却有有限的面积的几何图形。我们称产生的形状称为科赫雪花（Koch Snowflake）是一个自相似的分形。

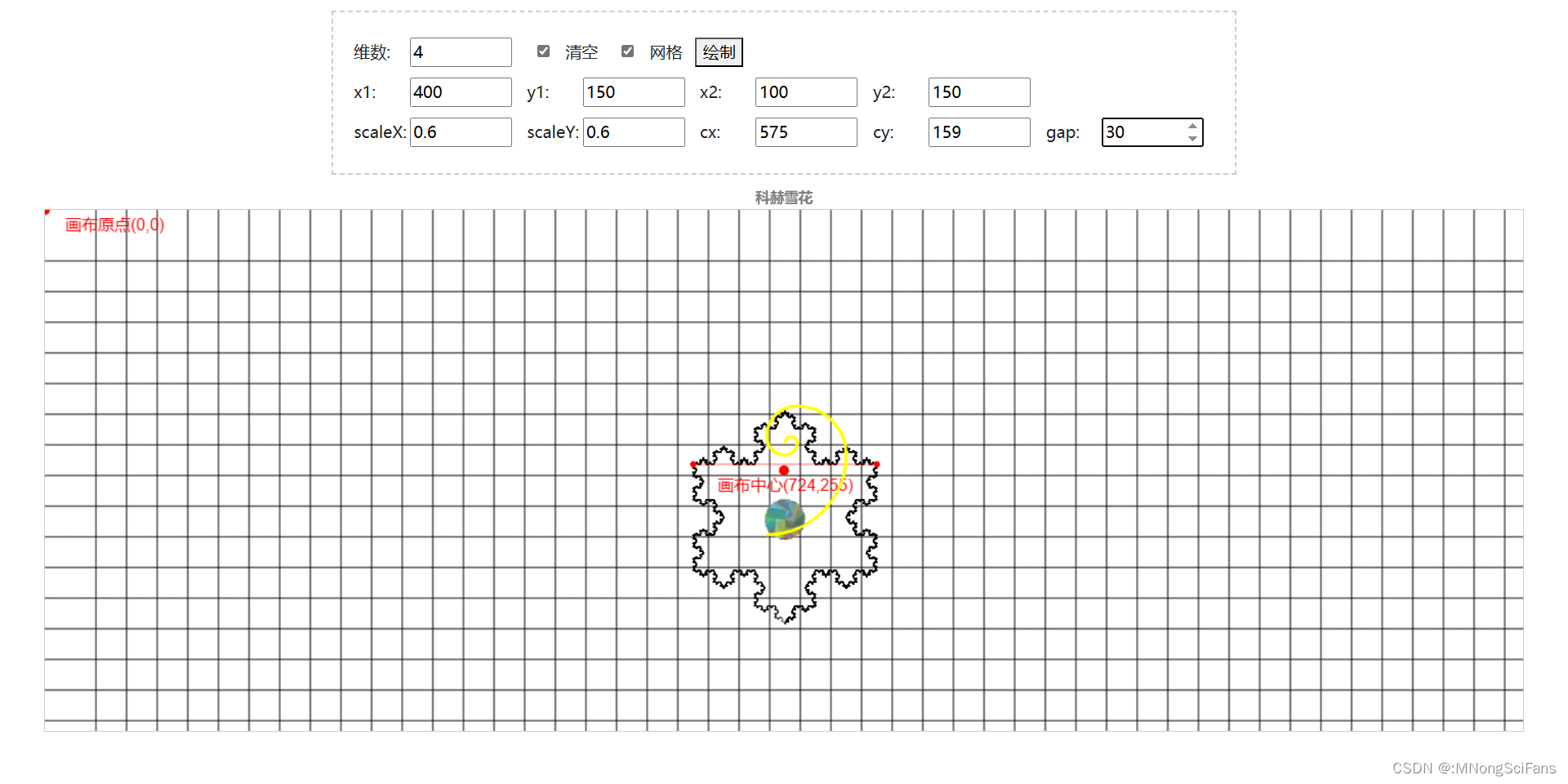
它由一个等边三角形组成，并在每个边上递归添加了较小的等边三角形。以