相对位姿估计

示意图

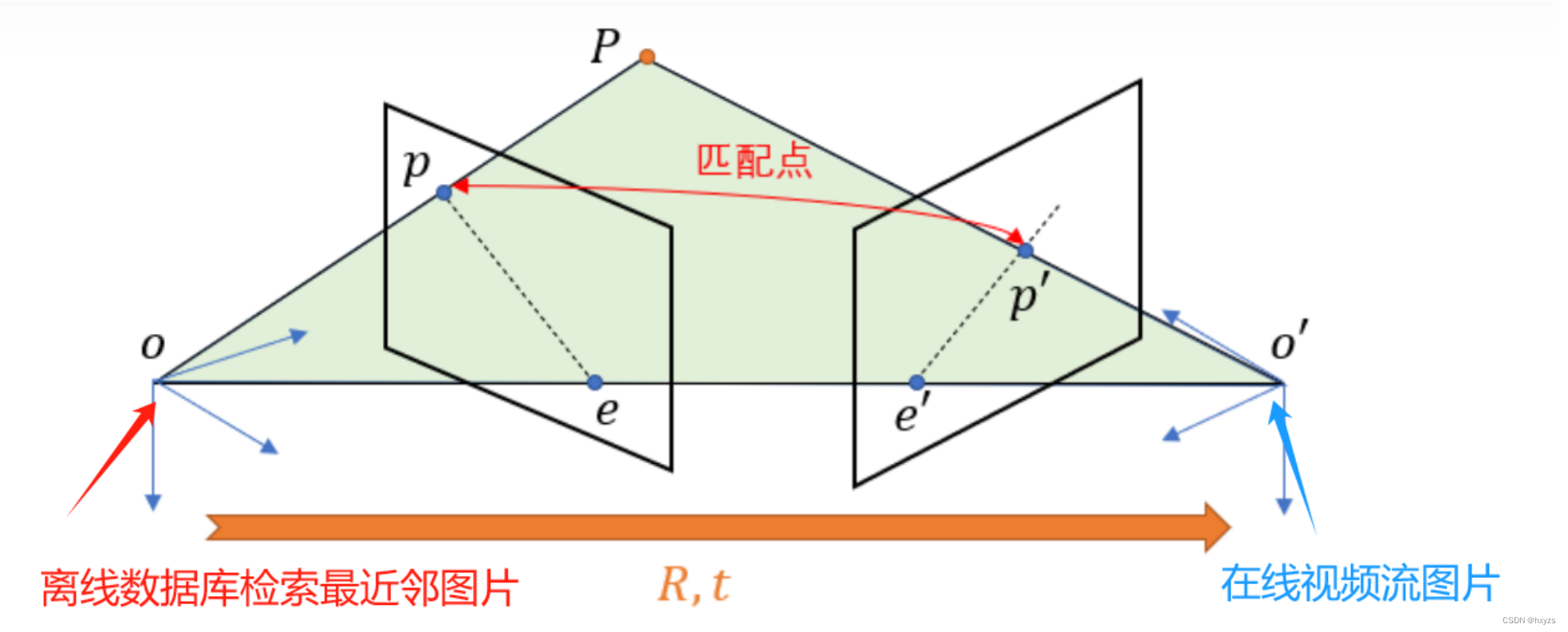
理论推导

离线数据库：

P的位置$$P=[X,Y,Z{]}^T$$

相机内参$$k_1$$

安卓手机：

相机内参$$k_2$$

两个像素点位置 ：$$p_1和p_2$$

公式一：

$$s_1{p}_1=K_{1}P$$ $$s_2{p}_2=K_2(RP+t)$$

**公式二：**归一化平面上的坐标

$$x_1=K_1^{-1}{p}_1$$ $$x_2=K_2^{-1}p2$$

公式三：

$$x_2=R{x}_1+t$$

公式四：

$$\hat{t}{x}_2=\hat{t}R{x}_1$$

公式五

$$x_2^T\hat{t}{x}_2=x_2^T\hat{t}R{x}_1$$

$$x_2^T\hat{t}R{x}_1=0$$

公式六：

$$(K_2^{-1}{p}_2{)}^T\hat{t}R{K}_1^{-1}{p}_1$$

结论：

本质矩阵： $$E=\hat{t}R$$ ---------------------已知相机参数的情况下

基础矩阵： $$F=K_2^{-T}E{K}_1^{-1}$$ -----------未知相机参数的情况下

伪代码

input:image_src,k_src,image_dst,k_dst
output:R,t
1 feature_detect(image_src,image_dst)---->keypoints and deccriptors
2 feature_match(image_src,image_dst)---->matched_features
3 find_essentialmatrix(matched_keypoints,k_src,k_dst)----->essential_matrix
4 decompose_E(essentialmatrix)----->R,t
5 judge "left or right"

实现代码

import cv2
import numpy as np

def find_keypoints_and_descriptors(image):
    # 使用SIFT算法检测关键点和计算描述符
    sift = cv2.SIFT_create()
    keypoints, descriptors = sift.detectAndCompute(image, None)
    return keypoints, descriptors

def match_keypoints(descriptors1, descriptors2):
    # 使用FLANN匹配器进行关键点匹配
    FLANN_INDEX_KDTREE = 0
    index_params = dict(algorithm=FLANN_INDEX_KDTREE, trees=5)
    search_params = dict(checks=50)
    flann = cv2.FlannBasedMatcher(index_params, search_params)
    matches = flann.knnMatch(descriptors1, descriptors2, k=2)

    # 保留良好的匹配
    good_matches = []
    for m, n in matches:
        if m.distance < 0.7 * n.distance:
            good_matches.append(m)

    return good_matches

def estimate_relative_pose(keypoints1, keypoints2, good_matches, camera_matrix_src,camera_matrix_dst):
    # 提取匹配点对应的关键点
    src_pts = np.float32([keypoints1[m.queryIdx].pt for m in good_matches]).reshape(-1, 1, 2)
    dst_pts = np.float32([keypoints2[m.trainIdx].pt for m in good_matches]).reshape(-1, 1, 2)

    # 使用基础矩阵估计相机的相对位姿
    essential_matrix, _ = cv2.findEssentialMat(src_pts, dst_pts, camera_matrix_src, camera_matrix_dst)

    # 从基础矩阵中恢复旋转和平移矩阵
    _, R, t, _ = cv2.recoverPose(essential_matrix, src_pts, dst_pts, camera_matrix_src, camera_matrix_dst)

    return R, t

def determine_camera_direction(t):
    if t[0] > 0:
        print("相机偏向右侧")
    elif t[0] < 0:
        print("相机偏向左侧")
    else:
        print("相机方向正前方")

# # 示例平移向量
# t = np.array([[1.5], [0.2], [0.3]])  # 假设平移向量 t = [1.5, 0.2, 0.3]

# determine_camera_direction(t)

def main():
    # 加载两张图片
    image1 = cv2.imread('image1.jpg', cv2.IMREAD_GRAYSCALE)
    image2 = cv2.imread('image2.jpg', cv2.IMREAD_GRAYSCALE)

    # 假设你已知相机内参
    fx_src = 1000.0  # 举例：相机的焦距
    fy_src = 1000.0
    cx_src = 320.0  # 图像中心点的x坐标
    cy_src = 240.0  # 图像中心点的y坐标
    camera_matrix_src = np.array([[fx_src, 0, cx_src],
                              [0, fy_src, cy_src],
                              [0, 0, 1]])
    
    fx_dst = 1000.0  # 举例：相机的焦距
    fy_dst = 1000.0
    cx_dst = 320.0  # 图像中心点的x坐标
    cy_dst = 240.0  # 图像中心点的y坐标
    camera_matrix_dst = np.array([[fx_dst, 0, cx_dst],
                              [0, fy_dst, cy_dst],
                              [0, 0, 1]])

    # 检测关键点和计算描述符
    keypoints1, descriptors1 = find_keypoints_and_descriptors(image1)
    keypoints2, descriptors2 = find_keypoints_and_descriptors(image2)

    # 匹配关键点
    good_matches = match_keypoints(descriptors1, descriptors2)

    # 估计相机的相对位姿
    R, t = estimate_relative_pose(keypoints1, keypoints2, good_matches, camera_matrix_src,camera_matrix_dst)

    # 计算旋转矩阵的欧拉角
    angles = cv2.Rodrigues(R)[0]
    yaw = np.arctan2(angles[1, 0], angles[0, 0]) * 180.0 / np.pi

    # 判断相机的方向
    if yaw > 0:
        print("相机偏向右侧,您应该向左转")
    elif yaw < 0:
        print("相机偏向左侧，您应该向右转")
    else:
        print("相机方向正前方")
                
        






if __name__ == "__main__":
    main()