数据结构（八）二叉树、哈希查找

news2024/7/6 18:08:59

文章目录

一、树
- （一）概念
- - 1. 前序遍历：根左右
  - 2. 中序遍历：左根右
  - 3. 后序遍历：左右根
  - 4. 层序遍历：需要借助队列实现
- （二）代码实现：二叉树
- - 1. 结构体定义
  - 2. 创建二叉树
  - - 1. 注意点
    - 2. 代码实现
  - 3. 遍历二叉树
  - - 1. 注意点
    - 2. 代码实现
  - 4. 销毁树
  - - 1. 注意点
    - 2. 代码实现
二、哈希Hash
- （一）构造函数：保留除数法（质数除余法）
- （二）处理冲突的方法
- - 1. 开放地址法
  - 2. 链地址法
- （三）使用实例
- - 1. 功能需求
  - 2. 需求分析
  - 3. 代码实现
  - - （1）结构体定义
    - （2）

一、树

（一）概念

1. 前序遍历：根左右

先遍历根节点然后遍历左子树最后遍历右子树
一般用于创建一棵树时，因为得先有根节点，才能给根节点左右指针分配空间

2. 中序遍历：左根右

先遍历左子树然后遍历根节点最后遍历右子树
对于一颗有序的二叉树，使用中序遍历，可以得到一个有序的数列

3. 后序遍历：左右根

先遍历左子树然后遍历右子树最后遍历根节点
一般用于销毁一棵树时，因为需要先释放左右子树，才能释放根节点

4. 层序遍历：需要借助队列实现

根节点入队列，然后出队列前，先把要出的节点的左右子树

（二）代码实现：二叉树

1. 结构体定义

typedef struct _Node{
    char data; //数据域
    struct _Node *lchild; //左子树
    struct _Node *rchild; //右子树
}node_t;

2. 创建二叉树

1. 注意点

创建二叉树是按照前序的顺序来创建的
判断递归是否结束的语句，需要放在申请空间之前，否则如果申请空间后再执行递归结束，会造成内存泄漏

2. 代码实现

int create_tree(node_t **root){
    if(NULL==root) return -1;
    char data;
    printf("请输入节点数据：");
    scanf("%c",&data);
    getchar();//吃垃圾字符
    if('#'==data) return 0; //递归的出口

    *root=(node_t *)malloc(sizeof(node_t));
    if(NULL==*root) return -1;
    (*root)->lchild=NULL;
    (*root)->rchild=NULL;
    (*root)->data=data;
    //左子树
    create_tree(&((*root)->lchild));
    //右子树
    create_tree(&((*root)->rchild));
    return 0;
}

3. 遍历二叉树

1. 注意点

遍历二叉树，前序、中序、后序的区别仅在于调用函数的顺序，前序即先打印根节点，再打印左节点，最后打印右节点；中序则先打印左节点，再打印根节点，最后打印右节点；后序就是先打印左节点，再打印右节点，最后打印根节点

2. 代码实现

//前序遍历
int preorder(node_t *root){
    if(NULL == root) return -1;
    printf("%c ",root->data);

    preorder(root->lchild);
    preorder(root->rchild);
    return 0;
}

//中序遍历
int inorder(node_t *root){
    if(NULL == root) return -1;

    inorder(root->lchild);
    printf("%c ",root->data);
    inorder(root->rchild);
    return 0;
}

//后序遍历
int postorder(node_t *root){
    if(NULL == root) return -1;

    postorder(root->lchild);
    postorder(root->rchild);
    printf("%c ",root->data);
    return 0;
}

4. 销毁树

1. 注意点

销毁树要按照后续顺序销毁，即先销毁左右节点，最后再释放根节点

2. 代码实现

int destory_tree(node_t **root){
    if(NULL == root|| NULL==*root) return -1;
    //先销毁左右子树
    destory_tree(&((*root)->lchild));
    destory_tree(&((*root)->lchild));
    //销毁根节点
    free(*root);
    *root=NULL;
    return 0;
}

二、哈希Hash

理想的哈希查找方法：对于给定的key值不需任何比较就可以获取记录。
在建立记录表时，确定记录的key与其存储地址的关系，这个关系就是Hash函数，H(key)
下述仅介绍一种常用的方法

（一）构造函数：保留除数法（质数除余法）

基本思想：设一个Hash表空间长度为m，取一个不大于m的最大的质数p
公式表达：H(key)=key%p

（二）处理冲突的方法

冲突：表中某地址中已存放数据，但是另一个数据经过Hash函数后得到的地址与该地址相同
选取随机度好的Hash函数可以使冲突减少，但是很难完全避免

在处理冲突的过程中，可能发生一连串的冲突现象，即可能得到一个地址序列H1、H2……Hn，Hi∈[0，m-l]。
H1是冲突时选取的下一地址，而H1中可能己有记录，又设法得到下一地址H2……直到某个Hn不发生冲突为止。这种现象称为“聚积”，它严重影响了Hash表的查找效率

1. 开放地址法

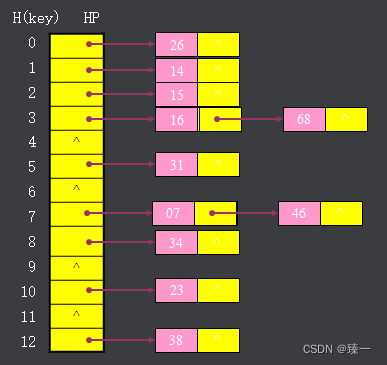
在这里插入图片描述
如下图，46%13=7，07%13=7，但是地址8已有数据，使用线性探查法，将07存到了地址9

但是这种方法可能会因为处理冲突占用空间而导致冲突产生，例如，如果此时再存入数据09，09%13=9，09本应该存在地址9，但是为了解决46和07的冲突，占用了地址9的位置，而导致冲突产生。还有可能发生聚积。