1. 引言

前序博客有：

• SNARK Design
• Rollup项目的SNARK景观

SNARK方案由 Polynomial IOP ➕多项式承诺方案 组成。

当前的Polynomial IOP主要分为三大类：

• 1）基于interactive proofs（IPs）的Polynomial IOP：如Hyrax、vSQL、Libra、Virgo等。【$P$无需做FFT运算】
• 2）基于multi-prover interactive proofs（MIPs）的Polynomial IOP：如Spartan、Brakedown、Xiphos等。【$P$无需做FFT运算】
• 3）基于constant-round的Polynomial IOP：如Marlin、PlonK、StarkWare的SNARKs等。【$P$需要做FFT运算】

以上方案都是通过增加$P$开销，来减少proof长度以及降低$V$开销。
以上1）2）类，只要其结合的多项式承诺方案也不需要FFT，则$P$无需做FFT运算。

当前的多项式承诺方案主要分为四大类：

• 1）基于pairing的多项式承诺方案（既不transparent，也不post-quantum）
  • 如KZG10、PST13、ZGKPP18等。
  • 独特属性有：具有constant sized evaluation proofs。
• 2）基于discrete logarithm的多项式承诺方案（transparent，但不post-quantum）
  • 如BCCGP16、Bulletproofs、Hyrax、Dory等。【其中Dory即需要discret-log hardness，还需要pairing。】
• 3）基于IOPs+hashing（transparent 且 post-quantum）
  • 如Ligero、FRI、Brakedown等。
• 4）基于Groups of unknown order的多项式承诺方案（若使用class groups具有transparent属性，但不是post-quantum的）
  • 如DARK、Dew等。
  • 由于使用class groups，$P$非常慢。

本文将：

• 1）从“Multi-prover Interactive Proofs”（即基于MIP）的Polynomial IOP 分类中选择一个示例
• 2）从“IOPs+hashing”的多项式承诺方案 分类中选择一个示例
• 3）将以上1）2）2个示例组合，展示SNARK的工作原理
• 4）将以上1）2）2个示例组合，所构成的SNARK具有novel efficiency：
  • 4.1）从文献来看，具有最快的$P$（concretely and asymptotically）；
  • 4.2）可基于任意（足够大）的域（即具有field agnosticism（域不可知）属性）；
  • 4.3）首个实现见Brakedown [GLSTW21]：
    • 详细见 Alexander Golovnev、Jonathan Lee、Srinath Setty、Justin Thaler和Riad S. Wahby等人2021年论文 Brakedown: Linear-time and post-quantum SNARKs for R1CS）
    • 开源代码见：https://github.com/conroi/lcpc（Rust）
  • 4.4）缺点在于：proof相当大——近期已对其进行了改进，可参看Tiancheng Xie等人2022年论文Orion: Zero Knowledge Proof with Linear Prover Time。【Orion改进了proof size，但是牺牲了field agnosticism（域不可知）属性。】
    

2. Polynomial IOP示例

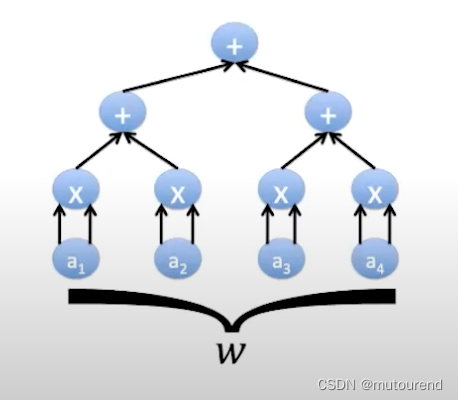
本文的Polynomial IOP示例运行在Arithmetic Circuit Satisfiability上下文中。
所谓Arithmetic Circuit Satisfiability，是指：

• 已知某 arithmetic circuit $C$ over $\mathbb{F}$ of size $S$且输出为$y$，判断是否存在某$w$，使得$C(w)=y$。