day17

news2024/11/18 1:49:29

第一题

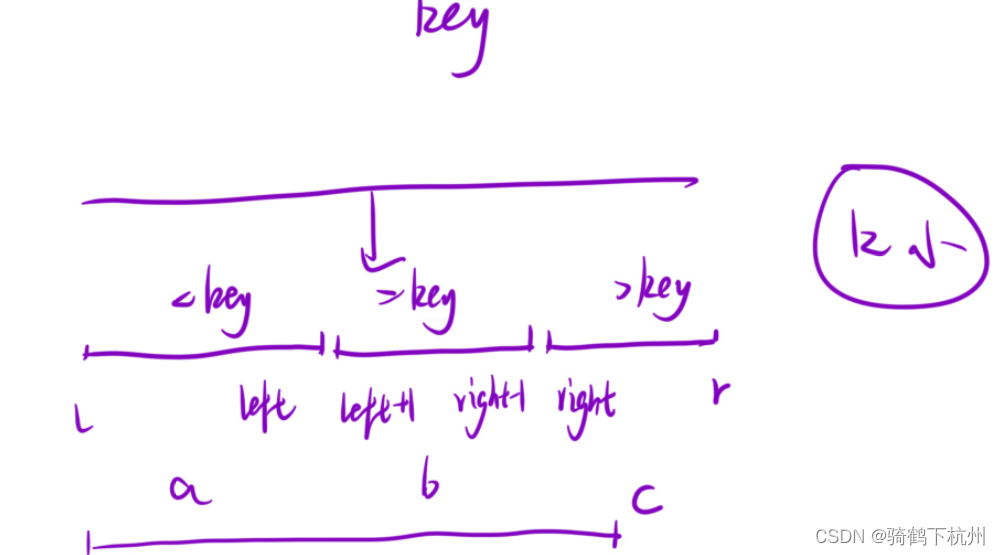
本题可以采用快速排序的思想，适应随机数指定和三指针划分数组为三个区域的思想：

其中指针的移动细节如上题故事，如下所示：

当a区域的商都大于k时，我们要查找的k位置元素就在左区域，我们进一步在左区域里面进一步划分区域和查找；

当a和b的长度大于k时，我们要查找的k位置元素就在中间区域，这时候直接返回区域中间的数值；

当上述的两个条件都不满足时，我们要查找的k位置元素就在右边区域，我们进一步在右区域里面进一步划分区域和查找第k-a-b小的元素；

综上所述，代码如下：
class Solution {
    public int[] getLeastNumbers(int[] nums, int k) 
    {
        qsort(nums, 0, nums.length - 1, k);
        int[] ret = new int[k];
        for(int i = 0; i < k; i++){
        ret[i] = nums[i];}
        return ret;
    }

    public void qsort(int[] nums, int l, int r, int k)
    {
        if(l >= r) return;
        // 1. 随机选择⼀个基准元素 + 数组分三块
        int key = nums[new Random().nextInt(r - l + 1) + l];
        int left = l - 1, right = r + 1, i = l;
        while(i < right){
            if(nums[i] < key) swap(nums, ++left, i++);
            else if(nums[i] == key) i++;
            else swap(nums, --right, i);
        }
        // 2. 分类讨论
        int a = left - l + 1, b = right - left - 1;
        if(a > k) qsort(nums, l, left, k);
        else if(a + b >= k) return;
        else qsort(nums, right, r, k - a - b);
    }
    public void swap(int[] nums, int i, int j){
        int t = nums[i];
        nums[i] = nums[j];
        nums[j] = t;
    }
}

第二题

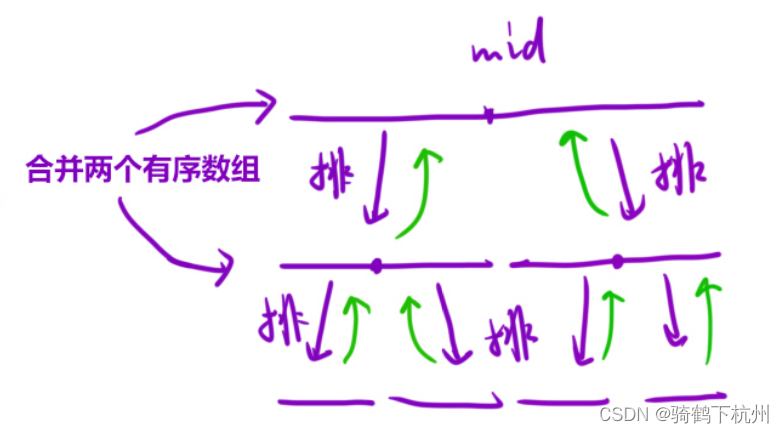
本题我们采用分治合并的思想，所谓的分支合并思想如下图所示：

首先将一个数组根据中间位置分成两个区域，左区域和右区域，记下来前往左区域将该区域已按照中间位置分为左1区域和右1区域，这样一直划分下去，直到最左边的区域到了划分极限返回开始处理每一层级的右区域也开始划分，直到不能划分为止，这时候就是用指针，两个区域两个指针开始比较每个指针所指的数，开始从小到大的排序，直到这一层数字有序之后开始返回上一层，继续使用双指针排序，直到最后一个上层，拍完之后将这些新数组中的数一一遍历到原数组中，即可；

代码如下：
class Solution {
    int[] tmp;
    public int[] sortArray(int[] nums) {
        tmp = new int[nums.length];
        mergeSort(nums,0,nums.length-1);
        return nums;
    }

    public void mergeSort(int[] nums,int left,int right){
        if(left >=right) return;
        int mid = (left + right)/2;
        mergeSort(nums,left,mid);
        mergeSort(nums,mid+1,right);

        int cur1 = left,cur2 = mid+1,i=0;
        while(cur1 <= mid && cur2 <= right){
            tmp[i++] = nums[cur1] <= nums[cur2] ? nums[cur1++] : nums[cur2++];
        }
        while(cur1 <= mid) tmp[i++] = nums[cur1++];
        while(cur2 <= right) tmp[i++] = nums[cur2++];
        // 4. 还原
        for(int j = left; j <= right; j++) 
            nums[j] = tmp[j - left];
    }
}