CF260E - Dividing Kingdom

$\mathrm{Description}$

给定 $n$ 个点 $(x_i,y_i)$ 和长度为 $9$ 的数列 $a$，满足 ${\sum }_{i=1}^n{a}_i=n$。通过 $2$ 条平行于 $x$ 轴的直线和 $2$ 条平行于 $y$ 轴的直线，将平面划分成 $9$ 个部分，第 $i$ 个部分点的数量记作 $b_i$。

输出一组解满足 $b$ 是 $a$ 的排列，或报告无解。

$9\le n\le 10^5,1\le x_i,y_i\le 10^9$

$\mathrm{Solution}$

观察到排列二字，$a$ 的长度还是 $9$，不难想到将 $a$ 进行全排列，对于每一种情况分别计算。

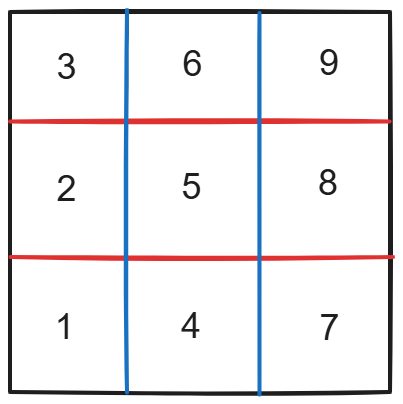
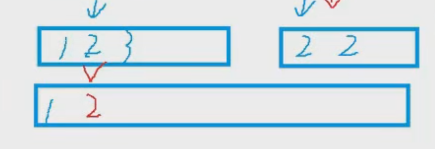
上图给出了划分，其中标号为 $i$ 表示格子内点数为 $a_i$。后面便需要对于 $a$ 的一种排列，初步确定出 $红色线$ 和 $蓝色线$ 的位置。不难发现，第 $1$ 根红线下面点数应为 $a_1+a_4+a_7$，第 $1$ 根红线至第 $2$ 根内点数应为 $a_2+a_5+a_8$（对于蓝线也同理，这里不过多赘述）。

故，通过二分可以快速确定红蓝线的位置。不过，按照如上的确定方式，一定能保证对应块满足条件吗？答案是否定的。还需要判断每个小方格内是否点数是匹配的，即相当于求若干个矩形内的点数，与 P2163 [SHOI2007] 园丁的烦恼 有异曲同工之处（这里不再细说）。

当你写完提交后，发现不是 $\mathrm{MLE}$，就是 $\mathrm{TLE}$。分析代码消耗时间最多处，能知晓是计算 $9$ 块常数太大，考虑优化。其实，由于前面特殊的划分方式，其实只需要计算 $1,3,5,7,9$ 块即可，大大降低了时空复杂度（这里请读者自行理解）。

综上所述，即可通过理论时间复杂度为 $O(n\log n+9!\log n)$ 的算法通过该题，不过由于常数过大，可以近似看做 $O(n{\log }^{2}n+9!\log n)$。

$\mathrm{Code}$

#include <bits/stdc++.h>
#define fi first
#define se second

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 2e5 + 10;

int n, m, k;
PII pnt[N];
int a[10], col[N], lin[N], qry[N * 20], idx, ans[4][N << 1];
std::vector<int> dct;
struct Query {
	int x, y, sign, id;
	bool operator< (const Query &tmp)const {
		if (y == tmp.y) {
			if (!sign) return 1;
			else if (!tmp.sign) return 0;
			return x < tmp.x;
		}
		return y < tmp.y;
	}
}q[N * 40];

int tr[N];
inline void add(int x, int d) { for (int i = x; i <= dct.size(); i += (i & -i)) tr[i] += d; }
inline int sum(int x) {
	int res = 0;
	for (int i = x; i; i -= (i & -i)) res += tr[i];
	return res;
}
inline int find(int x) {
	return lower_bound(dct.begin(), dct.end(), x) - dct.begin() + 1;
}
inline int binary(int aim, int v, int tmp[]) {
	int l = 1, r = dct.size();
	while (l < r) {
		int mid = l + r >> 1;
		if (tmp[mid] - v >= aim) r = mid;
		else l = mid + 1;
	}
	if (tmp[r] - v != aim) return -1;
	return r;
}
inline void add_query(int x1, int y1, int x2, int y2, int id) {
	q[ ++ idx] = {x2, y2, 1, id};
	if (x1 > 1) q[ ++ idx] = {x1 - 1, y2, -1, id};
	if (y1 > 1) q[ ++ idx] = {x2, y1 - 1, -1, id};
	if (x1 > 1 && y1 > 1) q[ ++ idx] = {x1 - 1, y1 - 1, 1, id};
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> n;

	for (int i = 1; i <= n; i ++ ) {
		cin >> pnt[i].fi >> pnt[i].se;
		dct.push_back(pnt[i].fi), dct.push_back(pnt[i].se);
	}

	sort(dct.begin(), dct.end());
	dct.erase(unique(dct.begin(), dct.end()), dct.end());

	for (int i = 1; i <= n; i ++)
		q[ ++ idx] = {find(pnt[i].fi), find(pnt[i].se), 0, 0};

	for (int i = 1; i <= 9; i ++)
		cin >> a[i];
	sort(a + 1, a + 10);

	for (int i = 1; i <= n; i ++)
		col[find(pnt[i].fi)] ++, lin[find(pnt[i].se)] ++;
	for (int i = 1; i <= dct.size(); i ++)
		col[i] += col[i - 1], lin[i] += lin[i - 1];

	do {
		int l1, l2, c1, c2;
		l1 = binary(a[1] + a[2] + a[3], 0, col);
		if (l1 == -1) continue;
		l2 = binary(a[4] + a[5] + a[6], col[l1], col);
		if (l2 == -1) continue;
		c1 = binary(a[7] + a[4] + a[1], 0, lin);
		if (c1 == -1) continue;
		c2 = binary(a[8] + a[5] + a[2], lin[c1], lin);
		if (c2 == -1) continue;
		ans[0][ ++ k] = l1, ans[1][k] = l2, ans[2][k] = c1, ans[3][k] = c2;
		qry[ ++ m] = a[3], add_query(1, c2 + 1, l1, dct.size(), m);
		qry[ ++ m] = a[9], add_query(l2 + 1, c2 + 1, dct.size(), dct.size(), m);
		qry[ ++ m] = a[5], add_query(l1 + 1, c1 + 1, l2, c2, m);
		qry[ ++ m] = a[1], add_query(1, 1, l1, c1, m);
		qry[ ++ m] = a[7], add_query(l2 + 1, 1, dct.size(), c1, m);
	}while (next_permutation(a + 1, a + 10));

	stable_sort(q + 1, q + 1 + idx);
	for (int i = 1; i <= idx; i ++)
		if (!q[i].sign)
			add(q[i].x, 1);
		else
			qry[q[i].id] -= q[i].sign * sum(q[i].x);

	for (int i = 1; i <= k; i ++) {
		bool flg = 1;
		for (int j = (i - 1) * 5 + 1; j <= i * 5; j ++)
			flg &= (!qry[j]);
		if (flg) {
			printf("%.1f %.1f\n%.1f %.1f\n", dct[ans[0][i] - 1] + 0.5, dct[ans[1][i] - 1] + 0.5, dct[ans[2][i] - 1] + 0.5, dct[ans[3][i] - 1] + 0.5);
			return 0;
		}
	}

	cout << -1 << endl;

	return 0;
}