平衡二叉树是二叉排序树的一种特殊情况,平衡二叉树的出现是为了在最坏情况下的时间复杂度仍然是对数级别O(logn),从而保证了高效的搜索、插入和删除操作。
举个例子,如果有一个数组是:1,2,3。如果只简单的排序:


如图所示,如果想要找到 3 这个元素,那么需要寻找 3 次,比较麻烦,如果换一种排序方式,如第二张图,仍然是二叉排序树,但是这次只需要寻找 2 次即可。
平衡二叉树(AVL)的特点是:
每个节点的左右子树的高度差最多为 1 。
那么如何实现左右子树的高度差只有 1 呢?这就需要引出文章的内容:四种操作,让普通排序二叉树变成平衡二叉树。
第一种,左旋(Left Rotation)
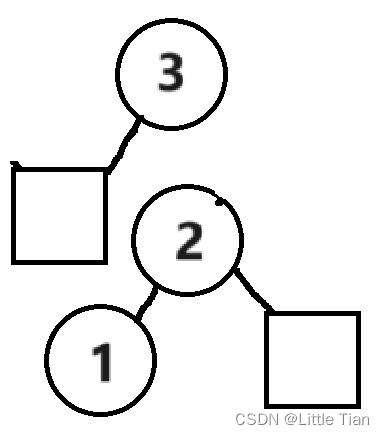
这种操作通常在左子树较高的情况下发生,如图,3 节点的左子树高度是2,右子树高度为0。我们要实现左图到右图的转变。
图中的方块是 2 节点的右子树,可以为空,如果存在,既然方块一开始就在 3 节点的左子树上,所以方块最后也一定在 3 的左子树。


现在我们可以思考一下具体操作,首先,把 2 的右孩子连接到 3 节点上(无论是否为空),然后把原来的根节点(3节点)连接到 2 节点上,最后更新根节点(变为 2 节点)。


代码如下:
void LL( TreeNode** root) {
TreeNode* node = NULL;
node = (*root)->lchild;
(*root)->lchild = node->rchild;
node->rchild = (*root);
(*root)->height = Max(GetTreeHeight((*root)->lchild), GetTreeHeight((*root)->rchild)) + 1;
node->height = Max(GetTreeHeight(node->lchild), GetTreeHeight(node->rchild)) + 1;
*root = node;
} 关于 Max 函数和 GetTreeHeight 函数我下篇文章会详细讲解,首先因为最后要改变根节点指针,所以传二级指针来改变根节点指针的值。旋转代码的关键就四行代码,红色箭头是找到 node 节点,即新的根节点,蓝色圈代表子树的重新构建,绿色箭头是代码的执行顺序。
第二种, 右旋(Right Rotation)
同理,右旋主要发生在右子树比较高的情况下,也就是文章最开始的图例。具体流程如下
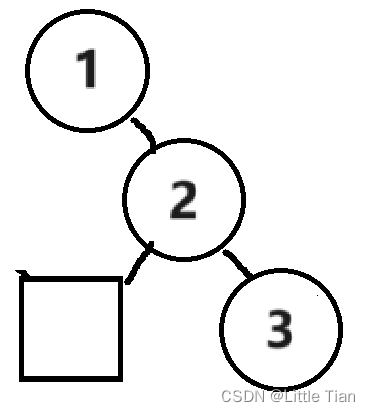

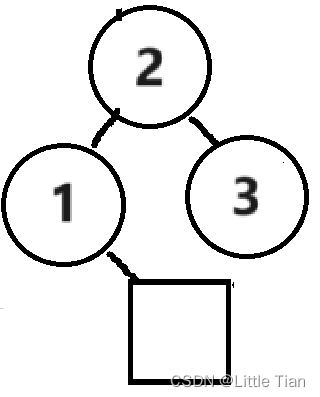
和左旋的原理一模一样,先把 2 节点的左孩子连接到原根节点上,然后把原根节点连接到 2 节点上,然后更新根节点,使 2 节点更新为新根节点,代码如下:
void RR( TreeNode** root) {
TreeNode* node = NULL;
node = (*root)->rchild;
(*root)->rchild = node->lchild;
node->lchild = (*root);
(*root)->height = Max(GetTreeHeight((*root)->lchild), GetTreeHeight((*root)->rchild)) + 1;
node->height = Max(GetTreeHeight(node->lchild), GetTreeHeight(node->rchild)) + 1;
*root = node;
}下面是过程图,逻辑和左旋相同,先保留 2 的左节点,更新 2 的左节点,最后更新根节点。

第三种,左-右旋(Left-Right Rotation)
如果二叉树是这种情况,此时 4 节点的左孩子高度为2,右孩子高度为0,此时需要变成右图中的情况。
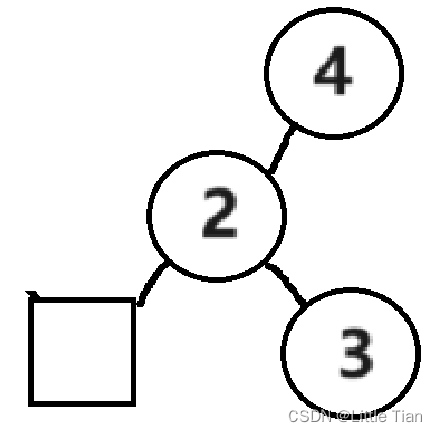

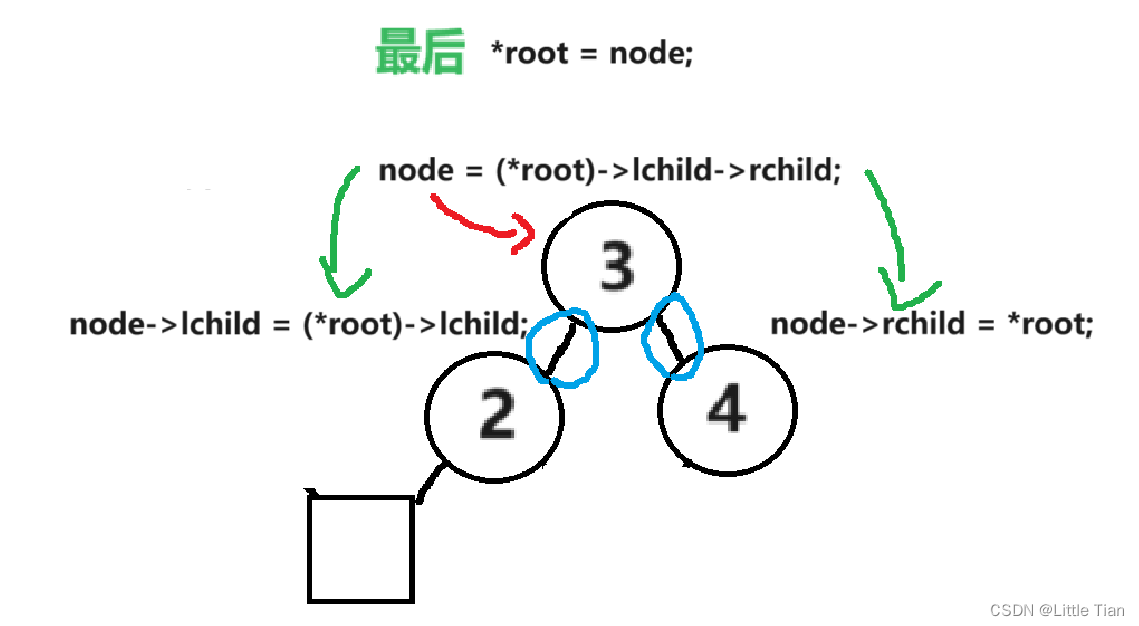
具体操作就是,把 2 节点连接到 3 节点的左孩子,4 节点连接到 3 节点的右孩子,最后更新根节点,使 3 节点变为根节点。
void LR(TreeNode** root) {
TreeNode* node = NULL;
node = (*root)->lchild->rchild;
node->lchild = (*root)->lchild;
node->rchild = *root;
(*root)->height = Max(GetTreeHeight((*root)->lchild), GetTreeHeight((*root)->rchild)) + 1;
node->height = Max(GetTreeHeight(node->lchild), GetTreeHeight(node->rchild)) + 1;
*root = node;
}下面是左右旋的流程图:
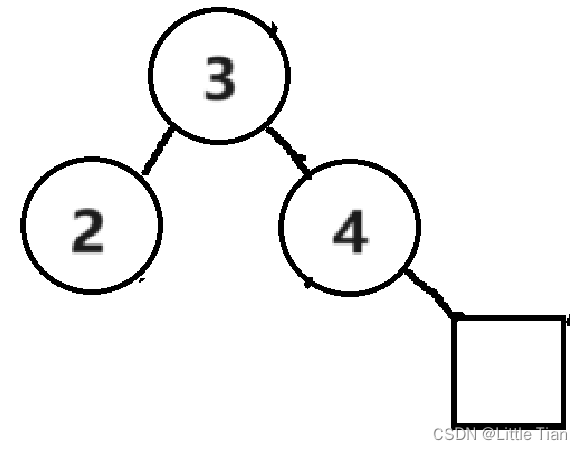
第四种,右-左旋(Right-Left Rotation)
第四种和第三种原理一样,只不过变成,把 4 节点连接到 3 节点的右孩子,2 节点连接到 3 节点的左孩子,最后更新根节点。

最后直接附上代码了:
void RL(TreeNode** root) {
TreeNode* node = NULL;
node = (*root)->rchild->lchild;
node->lchild = *root;
node->rchild = (*root)->rchild;
(*root)->height = Max(GetTreeHeight((*root)->lchild), GetTreeHeight((*root)->rchild)) + 1;
node->height = Max(GetTreeHeight(node->lchild), GetTreeHeight(node->rchild)) + 1;
*root = node;
}这就是文章的全部内容了,希望对你有所帮助,如有错误欢迎评论。