一、实验目的
1. 掌握MATLAB中进行IIR模拟滤波器的设计的相关函数的应用;
2. 掌握MATLAB的工具箱中提供的常用IIR数字滤波器的设计函数的应用;
3.掌握MATLAB的工具箱中提供的模拟滤波器转数字滤波器的相关的设计函数的应用。
二、实验内容
本实验为综合性实验项目,要求通过利用MATLAB软件编写程序,设计IIR数字滤波器,并绘制波形。
三、实验器材(设备、元器件)
安装有MATLAB软件的计算机1台。
四、实验步骤
1、设计一个工作于采样频率80 kHz的巴特沃斯低通数字滤波器,要求通带边界频率为4 kHz,通带最大衰减为0.5 dB,阻带边界频率为20 kHz,阻带最小衰减为45 dB。直接调用MATLAB工具箱函数buttord和butter设计数字滤波器,并显示数字滤波器系统函数H(z)的系数。
2、设计一个工作于采样频率80 kHz的切比雪夫Ⅰ型低通数字滤波器,要求通带边界频率为4 kHz,通带最大衰减为0.5 dB,阻带边界频率为20 kHz,阻带最小衰减为 45 dB。 直接调用MATLAB工具箱函数cheb1ord和cheby1设计数字滤波器,并显示数字滤波器系统函数H(z)的系数。
3、用脉冲响应不变法设计一个巴特沃斯低通数字滤波器,指标要求采样频率80 kHz,通带边界频率为4 kHz,通带最大衰减为0.5 dB,阻带边界频率为20 kHz,阻带最小衰减为45 dB。编写程序先调用MATLAB工具箱函数buttord和butter设计过渡模拟低通滤波器,再调用脉冲响应不变法数字化转换函数impinvar, 将过渡模拟低通滤波器转换成低通数字滤波器H(z)。
4、用双线性变换法(bilinear函数)设计符合以下指标的数字低通滤波器:通带内角频率低于0.2π rad时,容许幅度误差在1dB以内;在角频率0.3π到π之间的阻带衰减大于15dB,采样周期为0.5s。
五、实验程序及结果分析
1. 设计巴特沃斯低通数字滤波器代码如下:
close all;
clear all;
% 设置参数
Fs = 80000 ;% 采样频率
T = 1/Fs; %采样间隔
wp = 2 * pi * 4000/Fs; %%通带模拟角频率
ws = 2 * pi * 20000/Fs;%%阻带模拟角频率
rp = 0.5;
rs = 45;
% 进行设计
[N,wc] = buttord(wp/pi,ws/pi,rp,rs);
[B,A] = butter(N,wc)
% [Bz,Az] = impinvar(B,A,Fs)
% 绘图
figure;
subplot(2,2,1);
[H,w]= freqz(B,A,1000);
plot(w/pi,20*log10(abs(H)));
title('损耗函数曲线');
xlabel('\omega/\pi');
ylabel('幅度(dB)');
subplot(2,2,2);
plot(w/pi,angle(H));
title('相频特性曲线');
xlabel('\omega/\pi');
ylabel('相位');
axis([0 1 -2*pi 2*pi]);实验结果如下:
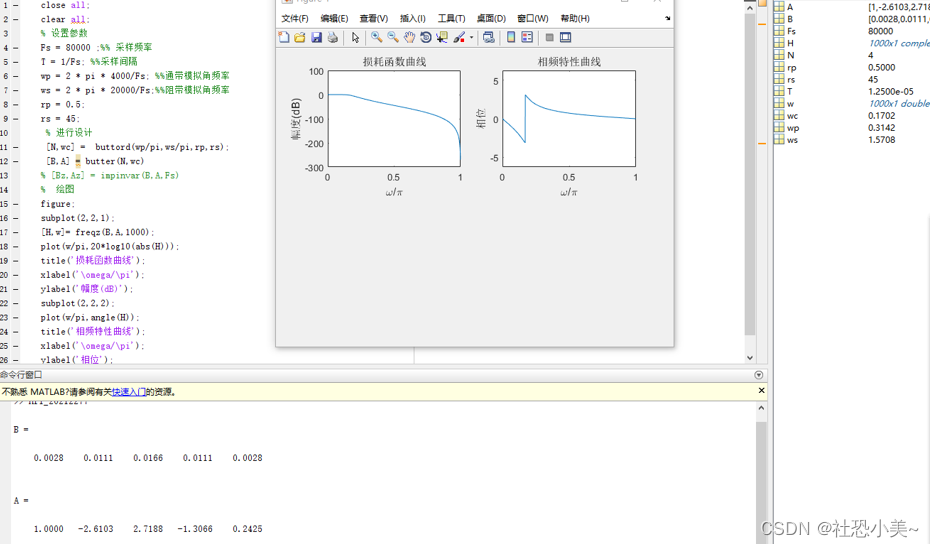
2.设计切比雪夫Ⅰ型低通数字滤波器代码如下:
close all;
clear all;
Fs = 80000; %Hz 采样频率
T = 1/Fs;
wp = 2 * pi * 4000/Fs; %%通带模拟角频率
ws = 2 * pi * 20000/Fs;%%阻带模拟角频率
rp = 0.5;
rs = 45;
%获取阶数和截止频率
[ N,wc ] = cheb1ord(wp/pi, ws/pi, rp , rs);
%获得转移函数系数
[ B,A ] = cheby1(N,rp,wc/pi,'low')
%滤波
figure;
subplot(2,2,1);
[H,w]= freqz(B,A,1000);
plot(w/pi,20*log10(abs(H)));
title('损耗函数曲线');
xlabel('\omega/\pi');
ylabel('幅度(dB)');
subplot(2,2,2);
plot(w/pi,angle(H));
title('相频特性曲线');
xlabel('\omega/\pi');
ylabel('相位');
axis([0 1 -2*pi 2*pi]);实验结果如下:
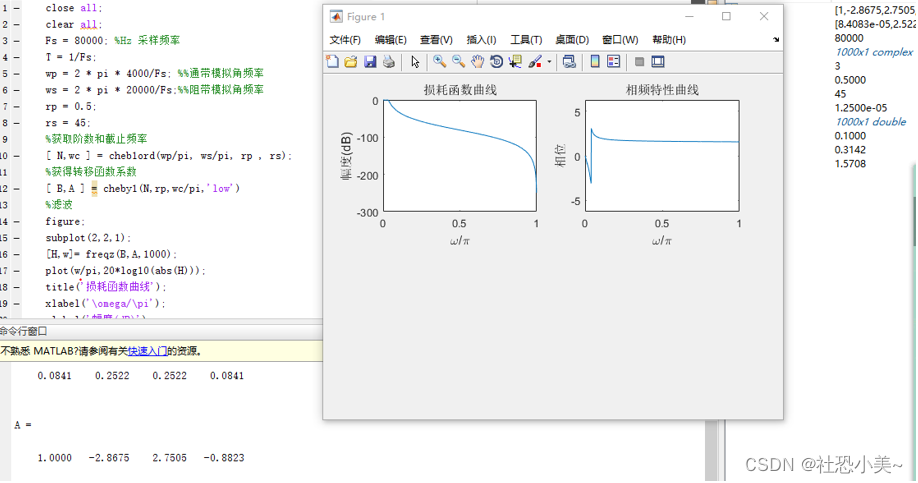
3.设计巴特沃斯低通数字滤波器代码如下:
close all;
clear all;
%1.数字滤波器的技术指标
rp = 0.5;%通带最大衰减
rs = 45;%阻带最小衰减
fp = 4000;%通带截止频率
fs = 20000;%阻带截止频率
Fs = 80000;%抽样间隔
T = 1/Fs;
%2.将数字指标转化成模拟滤波器技术指标(采用冲激响应不变法)
wap = 2*pi*fp;
was = 2*pi*fs;
%3.设计滤波器
[N,wac] = buttord(wap,was,rp,rs,'s');%计算阶数N和3dB截止频率wac
[z,p,k] = buttap(N);%创建巴特沃斯低通滤波器 z零点p极点k增益
[Bap,Aap] = zp2tf(z,p,k);%由零极点和增益确定归一化Han(s)系数
[Bbs,Abs] = lp2lp(Bap,Aap,wac);%将s/wc 代替s,去归一化
[B,A] = impinvar(Bbs,Abs,Fs);%模拟域到数字域——冲激响应不变法
[H1,w] = freqz(B,A);%根据H(z)求频率响应
%绘制数字滤波器频响幅度谱
figure(1);
f = w*Fs/(2*pi);
subplot(2,1,1);
plot(f,20*log10(abs(H1)));%绘制幅度响应
title('冲激响应不变法——巴特沃斯BLPF(幅度)');
xlabel('频率/Hz');
ylabel('H1幅值/dB');
subplot(2,1,2);
plot(f,unwrap(angle(H1)));% 绘制相位响应
xlabel('频率/Hz');
ylabel('角度/Rad');
title('冲激响应不变法——巴特沃斯BLPF(相位)'); 实验结果如下: 
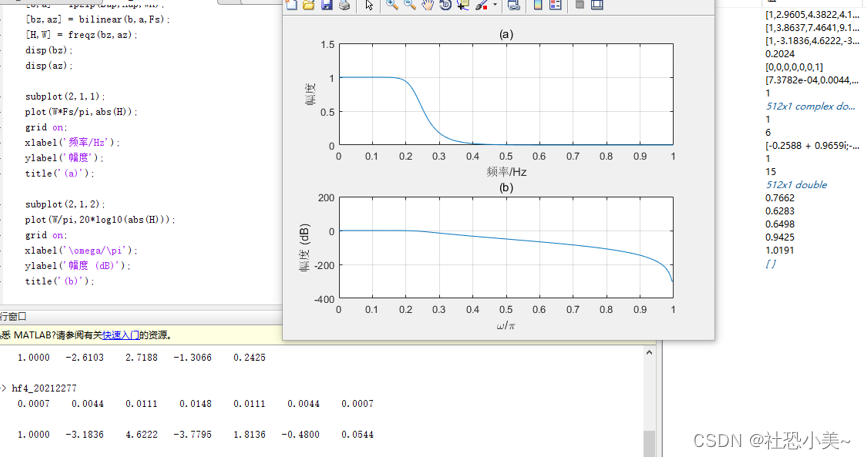
4.用双线性变换法设计数字低通滤波器代码如下:
clear all;
wp = 0.2*pi;
ws = 0.3*pi;
rp = 1;
rs = 15;
Fs = 1;
wp1=2*Fs*tan(wp/2);
ws1=2*Fs*tan(ws/2);
[N,Wn] = buttord(wp1,ws1,rp,rs,'s');
[Z,P,K] = buttap(N);
[Bap,Aap] = zp2tf(Z,P,K);
[b,a] = lp2lp(Bap,Aap,Wn);
[bz,az] = bilinear(b,a,Fs);
[H,W] = freqz(bz,az);
disp(bz);
disp(az);
subplot(2,1,1);
plot(W*Fs/pi,abs(H));
grid on;
xlabel('频率/Hz');
ylabel('幅度');
title('(a)');
subplot(2,1,2);
plot(W/pi,20*log10(abs(H)));
grid on;
xlabel('\omega/\pi');
ylabel('幅度 (dB)');
title('(b)');实验结果如下: