一、KNN算法的定义
KNN(K-Nearest Neighbors)算法,是一种简单而有效的监督学习方法。它既可以用在分类任务,也可用在回归任务中。KNN算法的核心思想:在特征空间中,如果有一个数据点周围的大多数邻居属于某个类别,则该数据点也应该被归为那么类别(分类任务中)。或者其预测值应该接近这些邻居的平均值(回归任务中)。
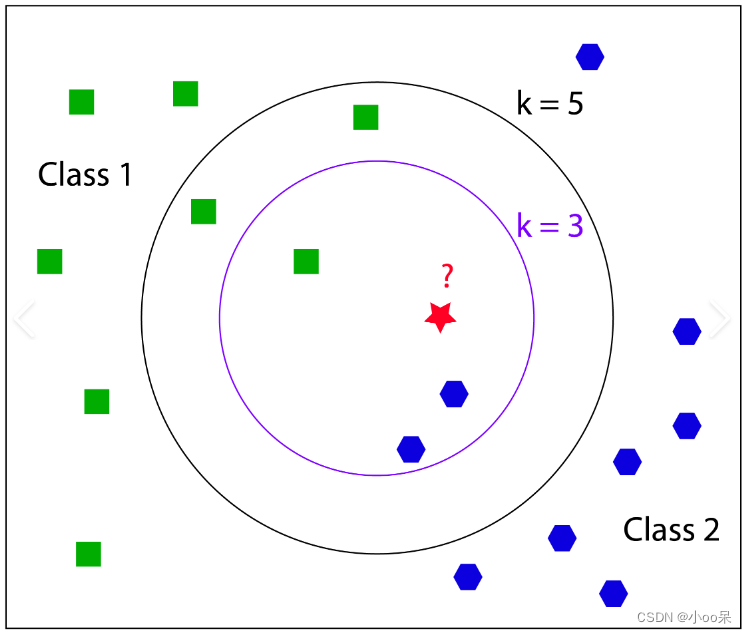
二、K值的选择
K是一个重要的超参数,其大小直接影响预测的准确性。
- K值较小可能导致过拟合,因为模型变得对噪声敏感;
- K值较大可能导致欠拟合,因为模型可能开始考虑远处的、不那么相关的邻居。
可以依据经验来选择,虽然经验可以在某些情况下提供指导,但确定K值通常依赖于更系统的方法。以下是几种常用的策略:
(1)依据经验
经验一:对于K的初试选择,K值常常在较小的范围内试探,比如从1开始,逐渐增加到如5、10、15等。这个范围的选择是为了平衡过拟合和欠拟合的风险。K值太小(如K=1)时,模型可能对噪声很敏感,容易过拟合;而K值太大时(比如大于训练样本数的平方根),模型可能会忽略局部特征,趋向于简单多数类,导致欠拟合。
经验二:如果数据集较小,K值通常不宜设置得太大,以免引入过多的噪声或稀释关键信息。相反,大数据集可能允许较大的K值。
经验三:有时推荐使用奇数K值以避免出现平票的情况,尤其是当类别分布较为均衡时。如果采用偶数K且遇到类别票数相同的情况,可能需要额外的规则来决定归属类别,如随机选择或考虑距离加权。
(2)交叉验证
这是一种常用的模型选择方法,也可以用来确定K值。具体操作是将数据集分割成训练集和验证集,然后对于每个候选的K值,使用训练集训练模型并在验证集上评估性能。重复这一过程,选择在验证集上表现最好的K值。

三、KNN算法步骤
(1)训练阶段
KNN算法非常不同,它的训练阶段不需要学习任何模型参数,它只是简单地存储所有的训练数据集,不做任何进一步的处理。
(2)预测阶段
① 数据准备与设置参数
收集数据:首先,需要有一组已经分类好的训练数据集,每条数据包括多个特征和对应的标签(分类任务)或数值(回归任务)。特征选择与标准化:选择对分类或回归有用的特征,并对数据进行预处理,如缩放特征值到同一尺度,以消除特征间因量纲不同造成的影响。选择K值:这是最重要的超参数之一,决定了在分类或回归时要考虑的最近邻居的数量。
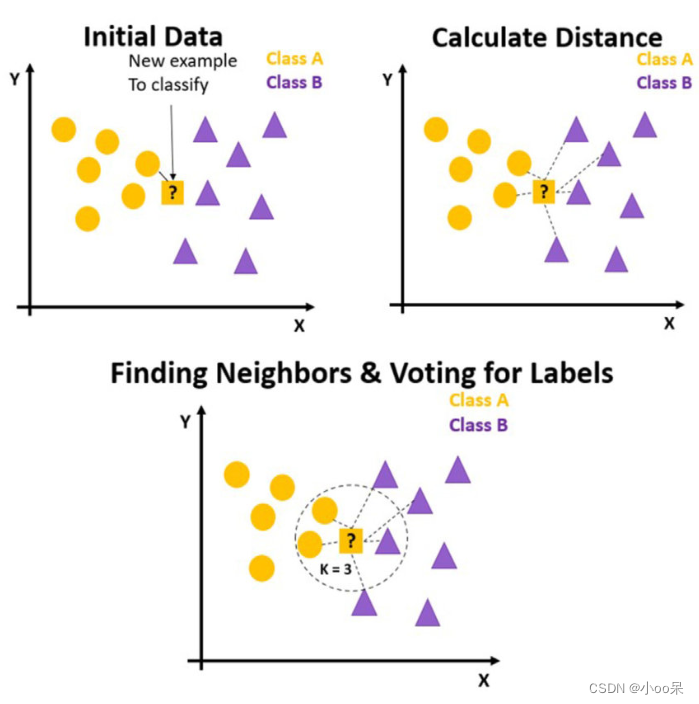
③ 计算距离
对于每一个新的未知类别的样本,计算其与训练集中每个样本之间的距离。常用的距离度量方法有欧氏距离、曼哈顿距离、切比雪夫距离等。
④ 选择邻居并做出决策
根据计算出的距离,找出距离最近的K个训练样本作为邻居。
- 分类任务:查看这K个邻居中哪个类别的样本最多,将新样本归为该类别。可以简单计数或距离加权(考虑距离远近)后决定。
- 回归任务:取这K个邻居的目标值的平均值(或加权平均)作为新样本的预测值。
⑤ 评估模型并优化调整
使用交叉验证或独立的测试集来评估模型的性能,包括准确率、召回率、F1分数等。根据评估结果,可能需要调整K值或考虑其他改进措施,如使用不同的距离度量方法、维度减少(如PCA)、或采用KD树等数据结构加速最近邻搜索。
四、KNN与K-means的关系
(1)KNN与K-means的区别
- 应用场景不同:KNN用于有监督学习的分类和回归问题,而K-means用于无监督学习的聚类任务。
- 对初始条件敏感性不同:K-means算法对初始聚类中心的选择非常敏感,不同的初始化可能导致完全不同的聚类结果。KNN算法则不受初始条件影响,因为它是基于查询点周围最近邻的直接比较,没有迭代优化聚类结构的过程。
- K的意义不同:在KNN中,K代表考虑的最近邻居的数量,直接影响模型的复杂度和预测的稳定性。较大的K值可以减少噪声的影响,但可能使边界变得模糊;较小的K值则可能对噪声敏感,但边界更清晰。在K-means中,K代表期望形成的簇的数量,需要事先指定,且选择合适的K值对聚类效果至关重要。错误的K值可能导致过分割或欠分割问题。
(2)KNN的优缺点
优点:简单易懂,原理直观,实现起来相对直接。无需训练,没有复杂的训练过程,计算负担主要在预测时。既能分类又能回归。
缺点:计算成本高,特别是对于大规模数据集,需要计算测试样本与所有训练样本之间的距离,非常耗时。存储需求大,需要存储整个训练数据集。对异常值敏感,训练数据中的异常点可能严重影响预测结果。特征尺度影响大,不同特征的尺度差异可能导致距离度量失真,通常需要进行特征缩放。