文章目录
- 一、递归
- (一)使用递归实现1~n求和
- 1. 代码实现:
- 2. 调用过程:
- 3. 输出结果:
- (二)青蛙跳台阶问题
- 1. 问题分析
- 2. 代码实现
- 3. 输出结果
- 4. 代码效率优化
- 5. 优化后的输出结果
- 二、快速排序
- (一)概念
- (二)基本思想
- (三)排序流程
- (三)代码实现
一、递归
递归就是在函数内部继续调用自身的逻辑。
注:
- 递归的本质就是函数调用,他并不是C语言程序结构的一种。
C语言的程序结构只有三种:循序结构、分支(选择)结构、循环结构 - 每个递归必须有一个出口,否则函数无限次调用下去,会把内存资源耗尽,导致堆栈溢出,出现段错误
(一)使用递归实现1~n求和
1. 代码实现:
#include <stdio.h>
//计算 1~n 的求和结果 并返回
int my_sum(int n){
if(1 == n) return 1;
return my_sum(n-1) + n;
}
int main(int argc, char const *argv[])
{
int ret = my_sum(100);
printf("sum = %d\n", ret);
return 0;
}
2. 调用过程:
以n=5为例,
首先在main函数中调用my_sum(5)
my_sum(5)的返回值是my_sum(4)+n,
因此会继续调用my_sum(4),my_sum(4)的返回值是my_sum(3)
继续调用my_sum(3),my_sum(3)的返回值是my_sum(2)
继续调用my_sum(2),my_sum(2)的返回值是my_sum(1)
当n==1时,即是递归函数的出口,返回1给my_sum(2),
my_sum(2)的返回值即是2+1=3,返回3给my_sum(3),
my_sum(3)的返回值是3+3=6,返回6给my_sum(4),
my_sum(4)的返回值就是6+4=10,返回10给my_sum(5),
最后得到my_sum(5)的结果就是10+5=15,返回15给main函数。
3. 输出结果:

(二)青蛙跳台阶问题
共有10阶台阶,青蛙每次只能跳1阶或者2阶
问:青蛙跳上这10阶台阶,共有多少种跳法?
1. 问题分析
跳上10阶台阶的方法等于从第8阶台阶跳上10阶和从第9阶台阶跳上10阶的方法之和,跳上9阶台阶的方法等于从第8阶台阶和从第7阶台阶跳上9阶的方法之和,然后依次类推…
当计算跳上1阶台阶的方法时,就是1种,跳上2阶台阶的方法就是2种,这时就是递归函数的出口
2. 代码实现
#include <stdio.h>
//定义一个全局变量用于记录函数调用次数
int count = 0;
//功能:计算跳上n阶台阶的跳法之和 返回计算的结果
int func(int n){
count++;
//递归的出口
if(1 == n) return 1;
if(2 == n) return 2;
return func(n-1) + func(n-2);
}
int main(int argc, const char *argv[])
{
int ret = 0;
ret = func(10);
printf("ret = %d\n", ret);
printf("count=%d\n",count);
return 0;
}
3. 输出结果

4. 代码效率优化
如果只是用递归,会有大量重复运算,效率会比较低
可以以空间换时间,保存已经计算过的值来提高效率
#include <stdio.h>
#define NUM_JUMP 10 //台阶数量
//定义一个全局变量用于记录函数调用次数
int count = 0;
//定义一个数组用于保存调用函数的值,保存跳上每阶台阶的方法
int sum[NUM_JUMP]={0};//数组的值全部初始化为0
int my_jump(int n){
count++;
if(n==1) return 1;
if(n==2) return 2;
if(sum[n]) return sum[n]; //当sum[n]不为空时,说明已经计算过该值,可以直接返回
//如果sum[n]==0时,说明该值没计算过,计算该值并保存到sum数组中
sum[n]=my_jump(n-1)+my_jump(n-2);
return sum[n];
}
int main(int argc, char const *argv[])
{
int ret = my_jump(10);
printf("jump = %d\n", ret);//89
printf("count = %d\n",count);
return 0;
}
5. 优化后的输出结果

可见优化后的函数调用次数远远小于优化前的函数调用次数,牺牲部分空间换来效率的提高
二、快速排序
(一)概念
快速排序相当于对冒泡排序的一个优化,也是基于交换的排序算法
时间复杂度 O(nlogn)
(二)基本思想
通过一趟排序,将待排序数据分成两部分,其中一部分数据都比另一部分小,而这两部分数据的内部不要求有序;
然后再对这两部分数据做同样的操作,也各自分成一大一小两部分,依次类推,直到整个数据组有序
(三)排序流程
定义两个下标变量,分别指向待排序的数组段的头和尾
以下图为例:
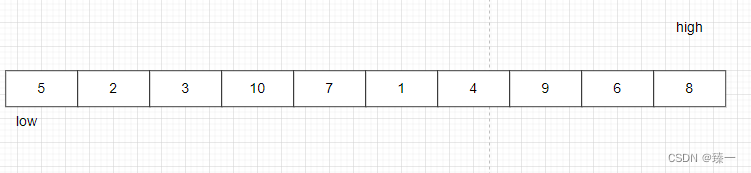
定义一个flag变量记录左侧第一个元素flag=arr[low](为了编程方便,也可以记录右侧第一个元素),然后从右向左开始依次比较flag和数组元素的大小
注:此处不要写成flag=arr[0]; 因为之后要对左右半边分别递归使用该函数,当对右半边排序时,应该使flag等于右半边的最左侧的数
如果flag<arr[high],就执行high- -,即下标high向左移动
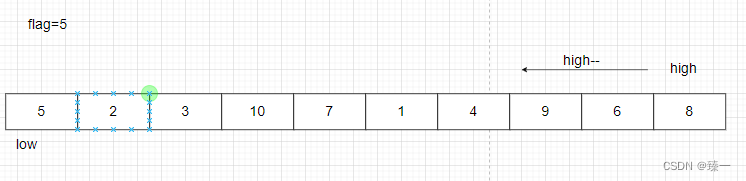
如果flag>arr[high],就执行arr[low]=arr[high],low++,但是前提条件是low<high

此时再从左往右依次比较flag和arr[low]的大小
如果flag>arr[low],就执行low++
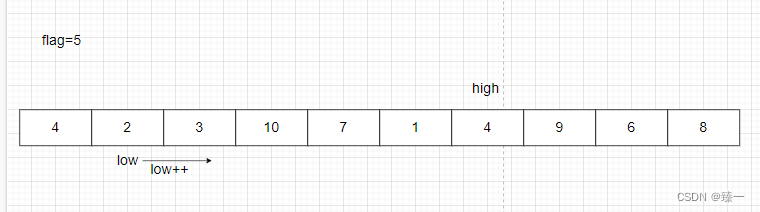
如果flag<arr[low],就执行arr[high]=arr[low],high- -,但是前提条件是low<high
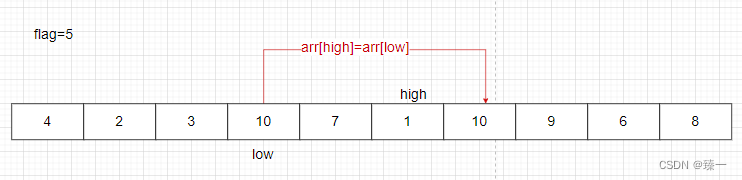
循环上述两个步骤直到low==high时,将arr[low]=flag或者arr[high]=flag
此时flag左边都是比flag小的数,flag右边都是比flag大的数,但是两侧无序
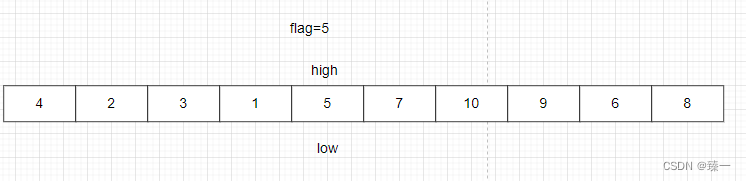
之后再对左半边和右半边分别排序
此处仅以右半边为例,左半边同理,只是low和high的值不同。
右半边:low=5,high=9(左半边:low=0,high=3)
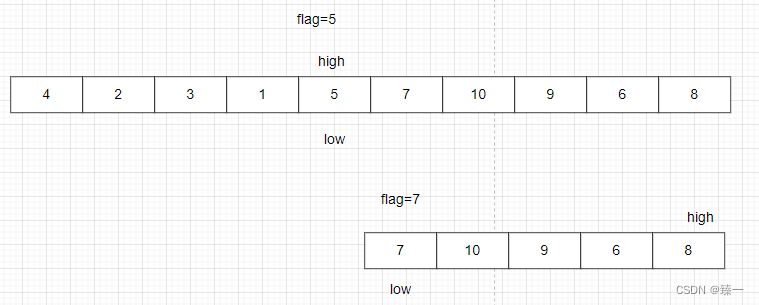
首先使flag=arr[low],此处为7
然后判断flag<arr[high]? 如果小于,就执行high- -
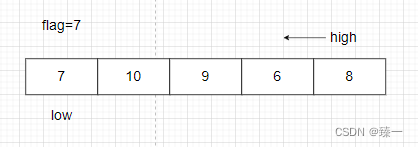
如果大于就执行arr[low]=arr[high],low++
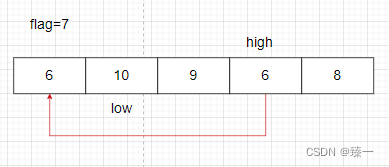
之后判断flag>arr[low]? 如果大于,就执行low++
如果小于就执行arr[high]=arr[low],high- -
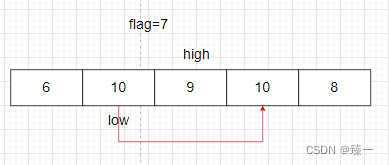
直到low==high时,arr[low]=flag或者arr[high]=flag
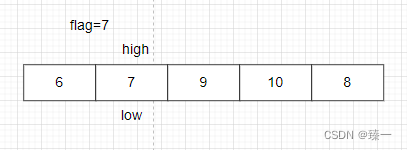
左半边同理,此处不再赘述。
(三)代码实现
#include <stdio.h>
int print(int *arr,int len){
if(NULL==arr) return -1;
for(int i=0;i<len;i++){
printf("%d ",arr[i]);
}
putchar(10);
return 0;
}
int my_sort(int *arr,int low,int high){
if(NULL==arr) return -1;
int flag=arr[low];
while(low < high){
while(flag<arr[high]&&low<high){
high--;
}
if(low<high){
arr[low]=arr[high];
low++;
}
while(flag>arr[low]&&low<high){
low++;
}
if(low<high){
arr[high]=arr[low];
high--;
}
}
arr[low]=flag;
return low;
}
int quick_sort(int *arr,int low,int high){
if(NULL==arr) return -1;
if(low < high){
int ret=my_sort(arr,low,high);
quick_sort(arr,low,ret-1);
quick_sort(arr,ret+1,high);
}
return 0;
}
int main(int argc, char const *argv[]){
int arr[10]={5,2,3,10,7,1,4,9,6,8};
printf("排序前:\n");
print(arr,10);
printf("排序后:\n");
quick_sort(arr,0,9);
print(arr,10);
return 0;
}