目录

1.奇数位丢弃

2.求和

3.计算字符串的编辑距离

---

1.奇数位丢弃

链接https://www.nowcoder.com/practice/196141ecd6eb401da3111748d30e9141?tpId=128&tqId=33775&ru=/exam/oj

数据量不大，可以直接进行模拟：

#include <iostream>
#include <vector>
using namespace std;

vector<int> v;
int n;
int main() {
    while(cin >> n)
    {
        // 每次都要清空数组
        v.clear();

        // 置数
        for(int i = 0; i <= n; ++i)
            v.push_back(i);

        while(v.size() > 1)
        {
            auto it = v.begin();
            while(it < v.end())
            {
                it = v.erase(it);
                if(it != v.end())
                    it++;
            }
        }
        cout << v[0] << endl;
    }
    return 0;
}

当然，也有更简便的方法：（找规律）

通过⼀两个例⼦的模拟，我们发现， 每次起始删除的下标都是 2 的次⽅。

根据这个规律，找到最后⼀次删除的起始位置的下标即可。

#include <iostream>
using namespace std;

int main()
{
    int n;
    while (cin >> n) // 多组输⼊
    {
        int ret = 1;
        while (ret - 1 <= n) ret *= 2;
        cout << ret / 2 - 1 << endl;
    }
    return 0;
}

2.求和

链接https://www.nowcoder.com/questionTerminal/af6d52eb400b40fd9652b089216f113e

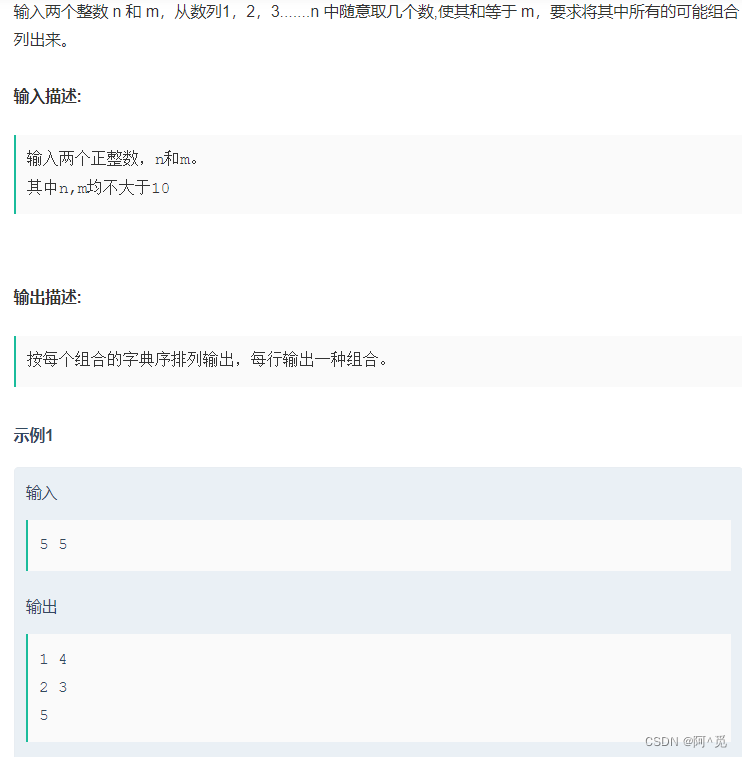
注意是随机取几个数，而不是只取两个，一开始我就看错了题目，直接双指针搜索了。

DFS：

找到路径和等于需要的值时打印即可：

题目明说，所以我们需要优先遍历选择的情况：

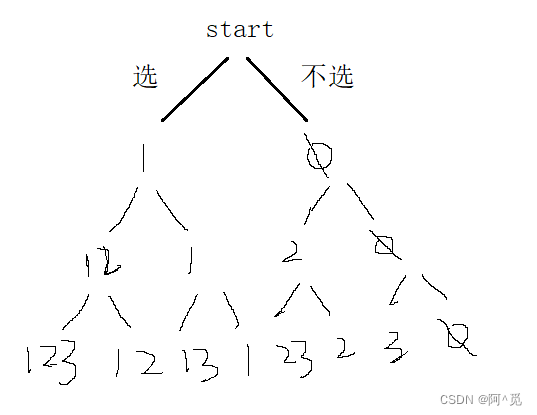
左边为选，右边为不选，以此类推（需要一个变量来存储路径和）

#include <iostream>
using namespace std;

int n, m;
bool vis[11];
int path;// 存储走过的路径和

void DFS(int pos)
{
    if(path == m)
    {
        for(int i = 1; i <= n; ++i)
            if(vis[i])
                cout << i << ' ';
        cout << endl;
        return;
    }
    if(path > m || pos > n) return;

    // 选pos
    path += pos;
    vis[pos] = true;
    DFS(pos + 1);
    path -= pos;
    vis[pos] = false;

    // 不选pos
    DFS(pos + 1);
}

int main()
{
    cin >> n >> m;  
    DFS(1);

    return 0;
}

3.计算字符串的编辑距离

链接https://www.nowcoder.com/practice/3959837097c7413a961a135d7104c314?tpId=37&tqId=21275&ru=/exam/oj

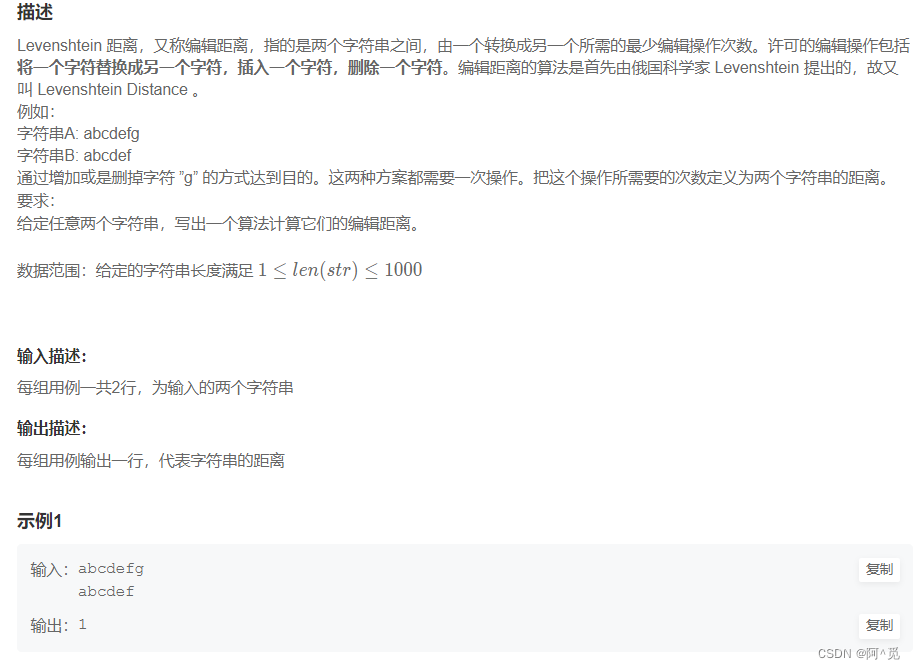
经典的二维dp问题：

当a[i] != b[j]时，在这三种情况中取最小值即可，因为有重复，所以可以简化，最后变为

min(dp[i - 1][j], min(dp[i][j - 1], dp[i - 1][j - 1])) + 1

还有就是注意初始化中的细节即可：

#include <iostream>
#include <string>
using namespace std;
const int N = 1010;

int dp[N][N];
char a[N];
char b[N];
int main() {
    string s1;
    string s2;
    cin >> s1 >> s2;
    int n = s1.size();
    int m = s2.size();

    // 填入char数组中，为了让下标从 1 开始
    for(int i = 1; i <= n; ++i)
        a[i] = s1[i - 1];
    for(int i = 1; i <= m; ++i)
        b[i] = s2[i - 1];

    // 初始化
    for(int i = 1; i <= n; ++i)
        dp[i][0] = i;
    for(int j = 1; j <= m; ++j)
        dp[0][j] = j;

    // 填表
    for(int i = 1; i <= n; ++i)
    {
        for(int j = 1; j <= m; ++j)
        {
            if(a[i] == b[j])
                dp[i][j] = dp[i - 1][j - 1];
            else
                dp[i][j] = min(dp[i - 1][j], min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
        }
    }

    // 返回
    cout << dp[n][m] << endl;
    return 0;
}