一、问题描述
拉格朗日插值及牛顿差商方法的实现。
二、实验目的
掌握拉格朗日插值和牛顿差商方法的原理,能够编写代码实现两种方法;能够分析多项式插值中的误差。
三、实验内容及要求
-
利用拉格朗日插值及牛顿差商方法估计1980 年的人口,并与1980 年的真实值
4452584592 进行比较,观察两种方法的结果是否相同。其中:
(a)利用1970 年和1990 年的数据,得到插值直线,估计1980 年的人口;
(b)利用1960 年、1970、1990 年的数据,得到插值抛物线,估计1980 年的人口;
(c)利用全部数据,估计1980 年的人口。
年份 人口
1960 3039585530
1970 3707475887
1990 5281653820
2000 6079603571 -
现有5 个插值节点:(0.6,1.433329), (0.7, 1.632316), (0.8, 1.896481), (0.9,2.247908), (1.0,2.718282)。
(a)使用牛顿差商方法计算 x = 0.82 和 x = 0.98 的近似值;
(b)上述数据来自函数f(x) = e(x2),使用插值误差公式找出x = 0.82 和x = 0.98 时的误差上界,比较误差界和实际误差。
(c)画出在区间[0.5, 1]上实际的插值误差曲线。
四、算法原理
1. 插值多项式的具体形式
拉格朗日插值多项式:
给定 n + 1 n+1 n+1个插值节点 ( x 0 , y 0 ) , ( x 1 , y 1 ) , . . . , ( x n , y n ) (x_0, y_0), (x_1, y_1), ..., (x_n, y_n) (x0,y0),(x1,y1),...,(xn,yn),拉格朗日插值多项式 L ( x ) L(x) L(x) 的表达式为:
L ( x ) = ∑ i = 0 n y i ⋅ ∏ j = 0 , j ≠ i n x − x j x i − x j L(x) = \sum_{i=0}^{n} y_i \cdot \prod_{j=0, j\neq i}^{n} \frac{x - x_j}{x_i - x_j} L(x)=∑i=0nyi⋅∏j=0,j=inxi−xjx−xj
其中, L ( x ) L(x) L(x) 是 n n n 次多项式,通过 n + 1 n+1 n+1 个插值节点, x x x 是待插值的点。
牛顿差商插值多项式:
给定 n + 1 n+1 n+1个插值节点 ( x 0 , y 0 ) , ( x 1 , y 1 ) , . . . , ( x n , y n ) (x_0, y_0), (x_1, y_1), ..., (x_n, y_n) (x0,y0),(x1,y1),...,(xn,yn),牛顿差商插值多项式 N ( x ) N(x) N(x) 的表达式为:
N ( x ) = y 0 + ( x − x 0 ) ⋅ f [ x 0 , x 1 ] + ( x − x 0 ) ⋅ ( x − x 1 ) ⋅ f [ x 0 , x 1 , x 2 ] + … + ( x − x 0 ) ⋅ ( x − x 1 ) ⋅ … ⋅ ( x − x n − 1 ) ⋅ f [ x 0 , x 1 , . . . , x n ] N(x) = y_0 + (x - x_0) \cdot f[x_0, x_1] + (x - x_0) \cdot (x - x_1) \cdot f[x_0, x_1, x_2] + \ldots + (x - x_0) \cdot (x - x_1) \cdot \ldots \cdot (x - x_{n-1}) \cdot f[x_0, x_1, ..., x_n] N(x)=y0+(x−x0)⋅f[x0,x1]+(x−x0)⋅(x−x1)⋅f[x0,x1,x2]+…+(x−x0)⋅(x−x1)⋅…⋅(x−xn−1)⋅f[x0,x1,...,xn]
其中,差商 f [ x i , x i + 1 , . . . , x j ] f[x_i, x_{i+1}, ..., x_{j}] f[xi,xi+1,...,xj] 的计算方式为:
f [ x i , x i + 1 , . . . , x j ] = f [ x i + 1 , x i + 2 , . . . , x j ] − f [ x i , x i + 1 , . . . , x j − 1 ] x j − x i f[x_i, x_{i+1}, ..., x_{j}] = \frac{f[x_{i+1}, x_{i+2}, ..., x_{j}] - f[x_i, x_{i+1}, ..., x_{j-1}]}{x_j - x_i} f[xi,xi+1,...,xj]=xj−xif[xi+1,xi+2,...,xj]−f[xi,xi+1,...,xj−1]
2. 多项式插值主定理
多项式插值主定理是插值理论的核心定理之一,它表述了一个多项式插值问题的存在唯一性。主定理陈述如下:
如果给定 n + 1 n+1 n+1 个节点 ( x 0 , y 0 ) , ( x 1 , y 1 ) , . . . , ( x n , y n ) (x_0, y_0), (x_1, y_1), ..., (x_n, y_n) (x0,y0),(x1,y1),...,(xn,yn),其中所有的 x i x_i xi 都是互不相同的,则存在唯一一个次数不超过 n n n 的多项式 P ( x ) P(x) P(x) 满足 P ( x i ) = y i P(x_i) = y_i P(xi)=yi,对所有的 i i i 成立。
3. 多项式插值中的误差公式和用途
误差公式:
多项式插值中的误差公式用于估计插值多项式与真实函数之间的误差。对于拉格朗日插值,误差公式为:
∣ f ( x ) − L ( x ) ∣ ≤ M ( n + 1 ) ! ⋅ ∏ i = 0 n ∣ x − x i ∣ |f(x) - L(x)| \leq \frac{M}{(n+1)!} \cdot \prod_{i=0}^{n} |x - x_i| ∣f(x)−L(x)∣≤(n+1)!M⋅∏i=0n∣x−xi∣
其中,
M
M
M 是插值区间内的最大二阶导数的上界。
对于牛顿差商插值,误差公式为:
∣ f ( x ) − N ( x ) ∣ ≤ M 4 ( n + 1 ) ⋅ ∏ i = 0 n ∣ x − x i ∣ |f(x) - N(x)| \leq \frac{M}{4(n+1)} \cdot \prod_{i=0}^{n} |x - x_i| ∣f(x)−N(x)∣≤4(n+1)M⋅∏i=0n∣x−xi∣
其中, M M M 是插值区间内的最大四阶导数的上界。
用途:
- 误差估计: 误差公式用于估计插值多项式的精度,帮助确定插值点的选择和插值多项式的次数。
- 数据逼近: 插值多项式可以用于逼近实际数据,使得在已知数据点上的拟合更为精确。
- 数值计算: 插值多项式在数值计算中广泛应用,例如在数值积分和数值微分等问题中。
综上所述,插值方法通过构造插值多项式在给定节点上与已知数据一致,提供了一种在非常有限数据点上估计未知函数值的方法,并通过误差估计帮助控制插值的精度。
五、测试数据及结果
- 针对(a)(b)(c)三种情况,分别给出拉格朗日插值及牛顿差商方法的估计值(保留4 位小数)。给出3 种情况下的误差(保留4 位小数),分析是否插值多项式次数越高,近似结果越好。
- 代码:
% 拉格朗日插值函数
function result = lagrange_interpolation(x, y, xi)
n = length(x);
result = 0;
for i = 1:n
term = y(i);
for j = 1:n
if j ~= i
term = term * (xi - x(j)) / (x(i) - x(j));
end
end
result = result + term;
end
end
% 牛顿差商方法函数
function result = newton_interpolation(x, y, xi)
n = length(x);
f = zeros(n, n);
f(:, 1) = y';
for j = 2:n
for i = 1:n-j+1
f(i, j) = (f(i+1, j-1) - f(i, j-1)) / (x(i+j-1) - x(i));
end
end
result = f(1, 1);
for j = 2:n
term = 1;
for i = 1:j-1
term = term * (xi - x(i));
end
result = result + f(1, j) * term;
end
end
- 结果:
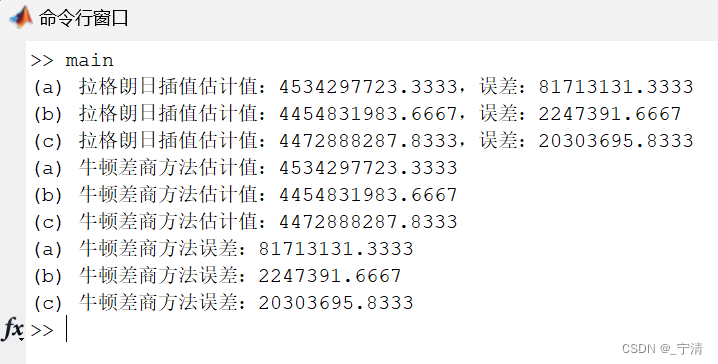
插值多项式次数越高,并不意味着近似结果一定越好。在插值中存在一个称为过拟合的问题,即使用高次多项式拟合数据,可能在已知数据点上表现得非常好,但在未知数据点上可能表现不佳。高次多项式在插值过程中容易产生振荡,尤其是在数据点边缘附近。这种情况下,多项式可能在数据点之间产生大的振荡,而不是真实的趋势。
- 按(a)(b)(c)的具体要求给出结果即可。
-
(a)&(b):
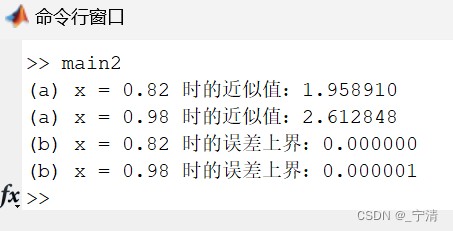
-
©:
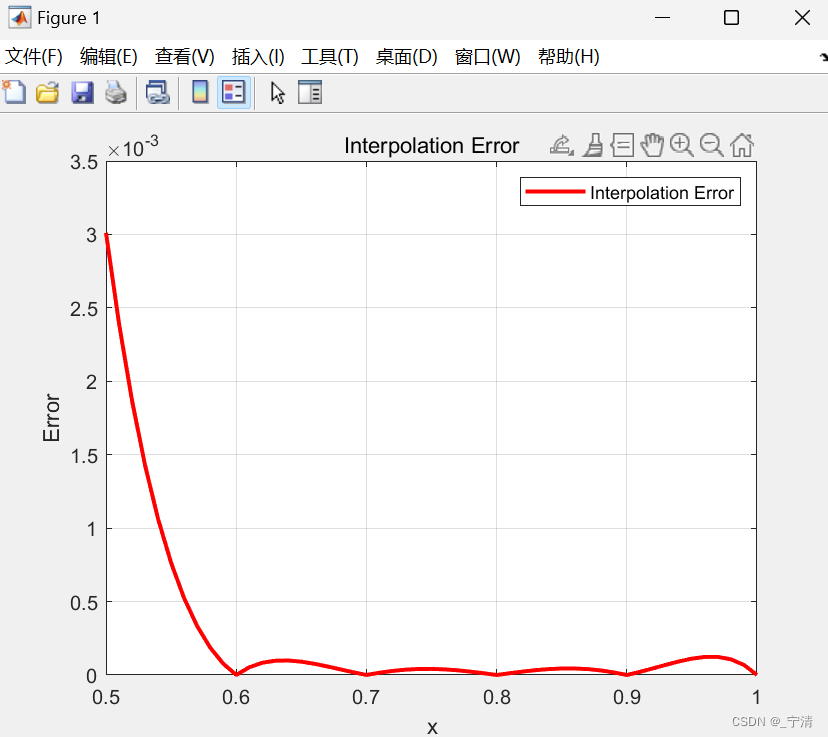
六、总结与思考
在实现拉格朗日插值和牛顿差商插值之前,深入理解了插值的基本原理是关键。插值的目标是通过已知数据点构建一个多项式,使得这个多项式在这些点上与真实函数相等。拉格朗日插值和牛顿差商插值是两种常见的插值方法,它们都基于多项式的性质,通过给定的插值节点生成插值多项式。
在编写和调试代码的过程中,遇到了一些错误,例如矩阵乘法的维度问题。这提醒了我在编写代码时要特别注意矩阵和数组的维度匹配,以避免出现运行时错误。同时,对于 MATLAB 的一些特殊语法和操作,要时刻保持警惕。
这次实验让我更深入地了解了插值方法的原理和应用,提高了对插值误差的理解。实践中遇到的问题促使我更加注重代码的细节和调试过程。通过这次实验,我对 MATLAB 编程、插值算法和数值计算的知识有了更全面的认识。在以后的学习和实践中,我将更加注重理论和实际问题的结合,提高编程和问题解决的能力。



![【Real】[Flask]SSTI](https://img-blog.csdnimg.cn/direct/a9a9d933f435421f88dee19186b79df5.png)