floodfill 算法（上）

news2024/11/18 12:34:43

目录

图像渲染

题意：

题解：

非递归：

递归：

岛屿数量

题解：

非递归：

递归：

岛屿的最大面积

题解：

非递归：

递归：

 被围绕的区域

题解：

非递归：

递归： 

图像渲染

733. 图像渲染 - 力扣（LeetCode）icon-default.png?t=N7T8https://leetcode.cn/problems/flood-fill/description/

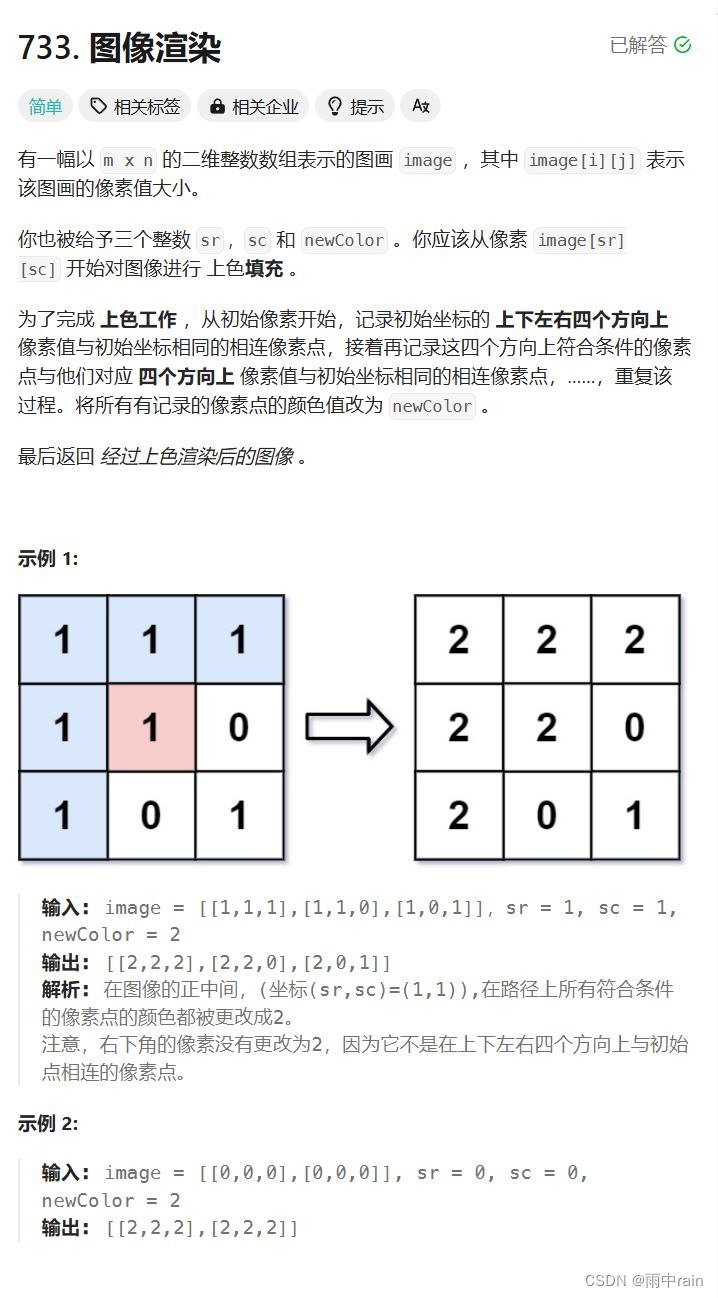
题意：

把初始位置的颜色作为标准值，如果其上下左右位置的颜色和标准值相同，就把该位置的颜色更改为 newColor，接着继续往外扩，重复上述操作。

题解：

这种题的思想类似树的层序遍历，我们从指定的坐标出发，查看上下左右的颜色，相当于查看外面一层的颜色，把需要染色的位置染色后，继续查看该位置外面一层的颜色。

思想类似，代码也类似。

我们定义一个队列，队列中存储需要修改颜色的位置的下标，便于层序遍历，先把初始位置入队：

1、取出队头 t ，并删除队头，接着修改 t 的颜色；

2、判断 t 的上、下、左、右是否需要修改颜色，如果需要修改，则把对应的位置入队；

3、在数组中，假设 t 的下标为 (x,y)，那么其上下左右的下标如图：

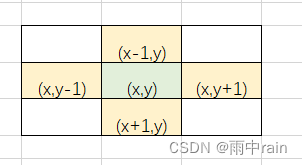
为了便于访问上下左右的位置，我们定义 dx、dy 数组，dx、dy 的同一个位置，对应着相对于 t 下标的偏移量，比如 t 的右边，可以看作 x 位置不变（相当于偏移了 0 个单位），y 向右偏移 1 个单位（+1），t 的左边，可以看作 x 位置不变，y 向左偏移 1 个单位（-1）。

int dx[4]={0,0,1,-1};//分别对应右、左、下、上
int dy[4]={1,-1,0,0};

我们只需要用 for 循环同时遍历这两个数组，就可以获得偏移量来计算上下左右的下标，但是这样的计算存在数组越界的风险，所以计算后的结果需要判断是否越界！ 

该算法会对同一个位置重复访问：

1、对于不需要修改颜色的位置，即使多次访问也不会修改颜色，并不影响最终结果；

2、对于需要修改颜色的位置，第一次访问时，已经更改颜色，所以颜色和 std 不一样了，后序再次访问，已经变成情况 1 了，不会再次更改颜色。

非递归：

class Solution {
public:
    vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {
        int std=image[sr][sc];
        if(std==color) return image;

        int dx[4]={0,0,1,-1};//分别对应右、左、下、上
        int dy[4]={1,-1,0,0};
        int m=image.size(),n=image[0].size();

        queue<pair<int,int>> q;
        q.push({sr,sc});

        while(!q.empty())
        {
            auto [x,y]=q.front();
            q.pop();
            image[x][y]=color;//修改像素
            for(int i=0;i<4;i++)
            {
                int x1=x+dx[i],y1=y+dy[i];//存入上下左右
                if(x1>=0 && x1<m && y1>=0 && y1<n && image[x1][y1]==std)
                {
                    q.push({x1,y1});
                }    
            }
        }

        return image;
    }
};

递归：

递归算法相当于在找需要修改颜色的下标时，一直向同一个方向递归，可以是一直向左、一直向右、一直向下、一直向上递归，直到这个颜色是不需要修改时，不再递归，再去判断其他方向是否需要修改颜色。

class Solution {
public:
    vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {
        if(image[sr][sc]==color) return image;
        int std=image[sr][sc];

        dfs(image,sr,sc,color,std);
        return image;
    }
    int dx[4]={0,0,1,-1};
    int dy[4]={1,-1,0,0};
    void dfs(vector<vector<int>>& image, int i, int j, int color,int std)
    {
        //修改当前格
        image[i][j]=color;
        for(int k=0;k<4;k++)
        {
            int x=i+dx[k],y=j+dy[k];
            //修改上下左右
            if(x>=0 && x<image.size() && y>=0 && y<image[0].size() && image[x][y] ==std)
                dfs(image,x,y,color,std);
        }

    }
};

岛屿数量

200. 岛屿数量 - 力扣（LeetCode）icon-default.png?t=N7T8https://leetcode.cn/problems/number-of-islands/description/

题解：

图像渲染是一个点不断向外扩展，这道题是多个点不断向外扩展，需要记录一共有多少个点源向外扩展了。

我们用两层 for 循环遍历数组，如果遍历到的位置是陆地，由于题目定义岛屿被水围绕，所以我们需要不断扩展，直到周围都是水，才停止扩展，此时岛屿数量+1。图像渲染即使对同一个位置重复访问也不会影响结果，而这道题同一个位置重复访问，结果会出现很大的错误！

以示例 1 为例，如左图，当我们访问 grid[ 0 ][ 0 ] 时，该位置为陆地，我们不断扩展，岛屿数量+1，当我们访问  grid[ 0 ][ 1 ] 时，该位置是陆地，但当前访问的陆地和上一次访问的陆地属于同一座岛屿，不能被认为是新的岛屿了！

我们设置一个和 grid 同等规模的 bool 类型的数组 vis，用于标记该陆地是否为未被发现的岛屿。

1、当 grid[ i ][ j ] 为陆地时，查看 vis[ i ][ j ] 的bool 值：

a. vis[ i ][ j ] 为 true，是已经被发现的岛屿，该陆地不可以被记为岛屿；

b. vis[ i ][ j ] 为 false，是未被发现的岛屿，可以记为新的岛屿，并且向外扩展，把相连的陆地的 vis 全部记为 true，直到周围都是水为止。

2、当 grid[ i ][ j ] 为水时，不需要做任何处理。

扩展的思路和图像渲染一样，这里不再赘述。

非递归：

class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        int m=grid.size(),n=grid[0].size();
        vector<vector<bool>> vis(m,vector<bool>(n));
        int ret=0;
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(grid[i][j]=='1' && !vis[i][j])
                {
                    ret++;
                    bfs(grid,vis,i,j,m,n);
                }
            }
        }
        return ret;
    }
    void bfs(vector<vector<char>>& grid,vector<vector<bool>>& vis,int i,int j,int m,int n)
    {
        int dx[4]={0,0,1,-1};
        int dy[4]={1,-1,0,0};
        queue<pair<int,int>> q;
        q.push({i,j});

        while(!q.empty())
        {
            auto [a,b]=q.front();
            q.pop();
            for(int k=0;k<4;k++)
            {
                int x=a+dx[k],y=b+dy[k];
                if(x>=0 && x<m && y>=0 && y<n && grid[x][y]=='1' && !vis[x][y])
                {
                    q.push({x,y});
                    vis[x][y]=true;
                }
            }
        }
    }
};

递归：

class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        vector<vector<bool>> vis(grid.size(),vector<bool> (grid[0].size()));

        int ret=0;
        for(int i=0;i<grid.size();i++)
        {
            for(int j=0;j<grid[0].size();j++)
            {
                if(grid[i][j]=='1' && !vis[i][j])
                {
                    ++ret;
                    dfs(grid,vis,i,j);
                }
            }
        }
        return ret;
    }
    int dx[4]={0,0,1,-1};
    int dy[4]={1,-1,0,0};
    void dfs(vector<vector<char>>& grid,vector<vector<bool>>& vis,int i,int j)
    {
        vis[i][j]=true;//修改当前格
        for(int k=0;k<4;k++)
        {
            int x=i+dx[k],y=j+dy[k];
            if(x>=0 && x<grid.size() && y>=0 && y<grid[0].size() && grid[x][y]=='1'&& !vis[x][y] )
                dfs(grid,vis,x,y);
        }
    }
};

岛屿的最大面积

695. 岛屿的最大面积 - 力扣（LeetCode）icon-default.png?t=N7T8https://leetcode.cn/problems/max-area-of-island/description/

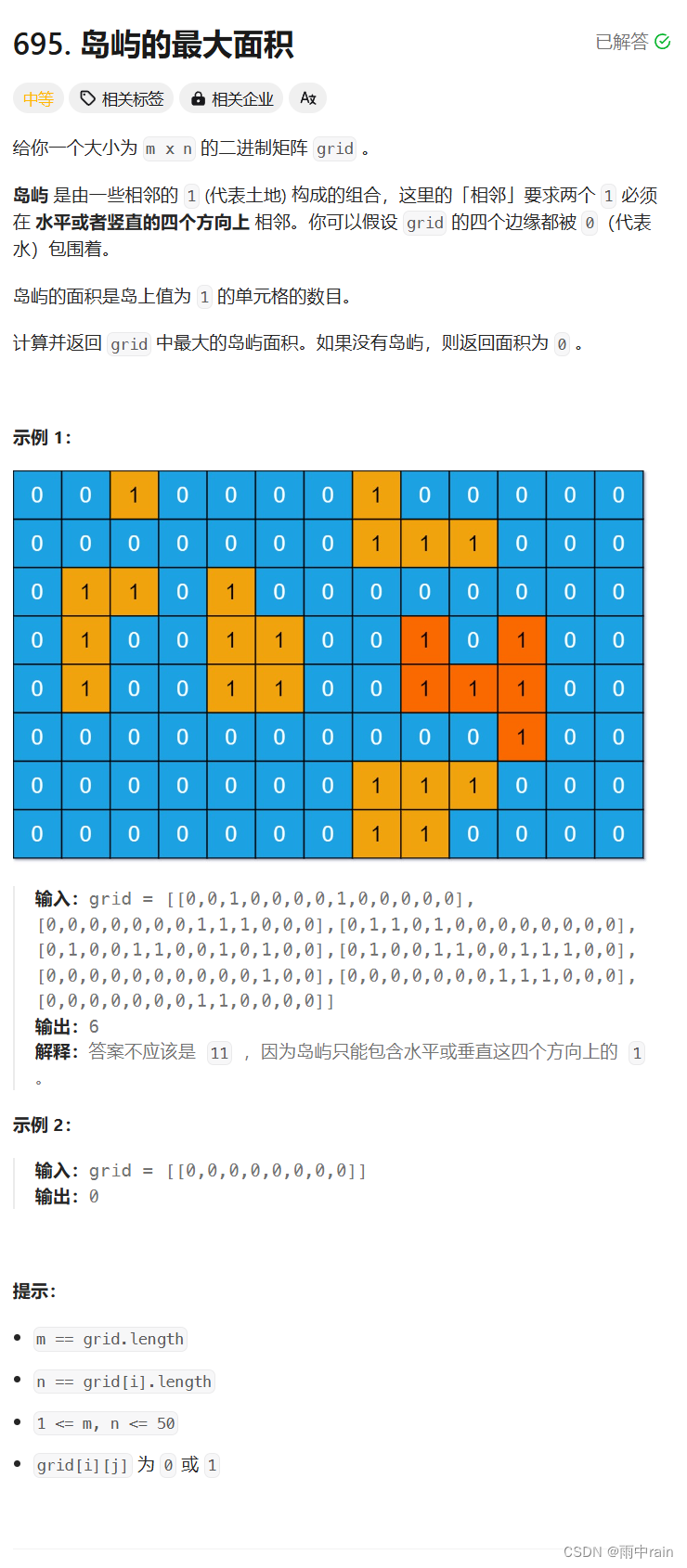
题解：

这道题只需要在每次扩展岛屿的陆地时，记录一共扩展了多少块陆地即可，同理对已经被发现的陆地，不可以重复计算。 

非递归：

class Solution {
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int ret=0,m=grid.size(),n=grid[0].size();
        vector<vector<bool>> vis(m,vector<bool>(n));
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(grid[i][j]==1 && !vis[i][j])
                {
                    int tmp=AreaOfIsland(grid,i,j,vis);
                    ret=max(ret,tmp);
                }
            }
        }
        return ret;        
    }

    int AreaOfIsland(vector<vector<int>>& grid,int i,int j,vector<vector<bool>>& vis)
    {
        int dx[4]={0,0,1,-1};
        int dy[4]={1,-1,0,0};
        queue<pair<int,int>> q;
        q.push({i,j});
        int area=1;
        //++area;
        vis[i][j]=true;
        while(!q.empty())
        {
            auto [a,b]=q.front();
            q.pop();
            for(int k=0;k<4;k++)
            {
                int x=a+dx[k],y=b+dy[k];
                if(x>=0 && x<grid.size() && y>=0 && y<grid[0].size() && grid[x][y]==1 && !vis[x][y])
                {
                    q.push({x,y});
                    vis[x][y]=true;
                    ++area;
                }
            }
        }
        return area;
    } 
};

递归：

class Solution {
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        vector<vector<bool>> vis(grid.size(),vector<bool>(grid[0].size()));
        int ret=0;
        for(int i=0;i<grid.size();i++)
        {
            for(int j=0;j<grid[0].size();j++)
            {
                if(grid[i][j]==1 && !vis[i][j])
                {
                    int tmp=0;
                    dfs(grid,vis,i,j,tmp);
                    ret=max(ret,tmp);
                }
            }
        }
        return ret;
    }

    int dx[4]={0,0,1,-1};
    int dy[4]={1,-1,0,0};
    void dfs(vector<vector<int>>& grid,vector<vector<bool>>& vis,int i,int j,int& area)
    {
        ++area;        
        vis[i][j]=true;//修改当前值
        for(int k=0;k<4;k++)
        {
            int x=i+dx[k],y=j+dy[k];
            if(x>=0 && x<grid.size() && y>=0 && y<grid[0].size() && grid[x][y]==1 && !vis[x][y])
                dfs(grid,vis,x,y,area);
        }        
    }
};

 被围绕的区域

130. 被围绕的区域 - 力扣（LeetCode）icon-default.png?t=N7T8https://leetcode.cn/problems/surrounded-regions/description/

题解：

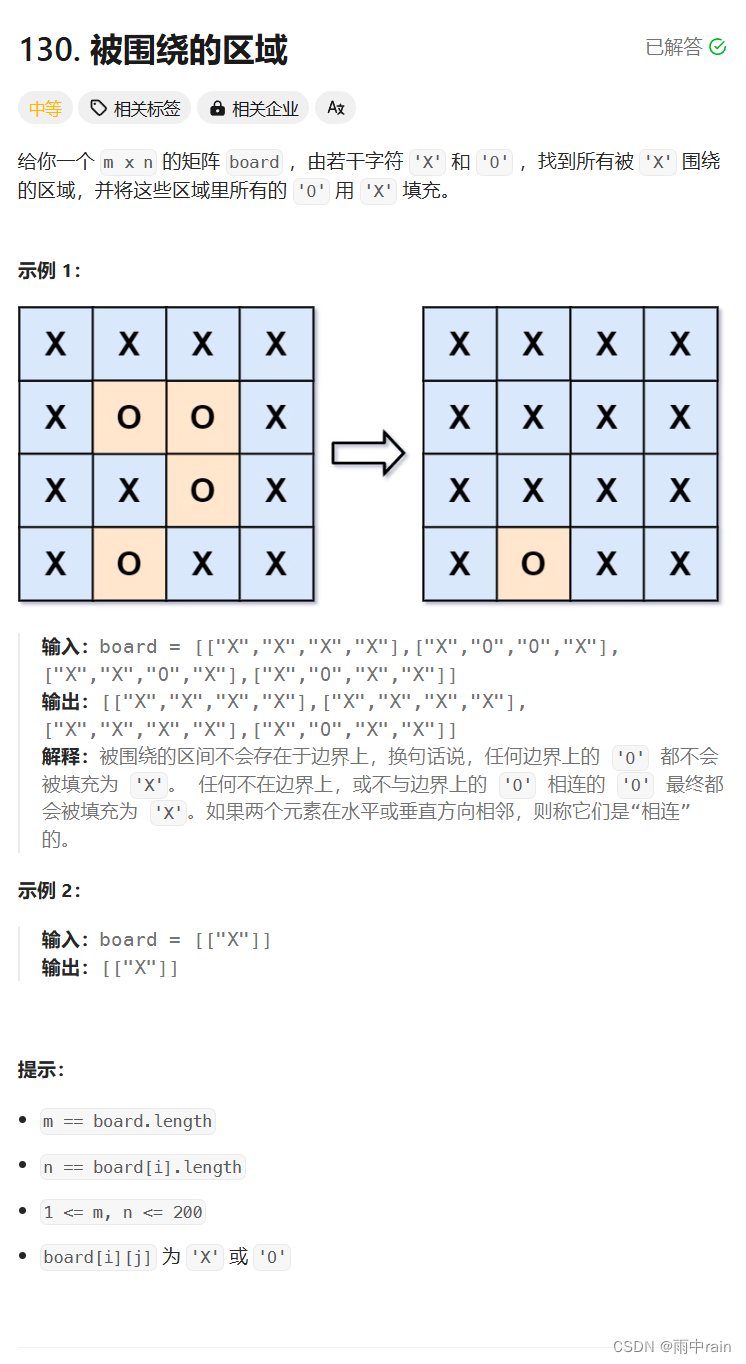
本道题和图像渲染类似，但是如果区域内的 O 与边界的 O 相连，那么这个 O 不可以被修改！这个特殊条件并不好处理。

1、我们可以优先处理和边界相连的 O：

可以设置一个和 board 相同规模的 bool类型的数组 vis，把和边界相连的 O 的对应位置的 vis 设置为 true。

2、用两层 for 循环遍历 board：

a. 如果 board[ i ][ j ] 为 O，且 vis[ i ][ j ] 为 false，说明这个 O 没有和边界的 O 相连，把它修改为 X；

b. 如果 board[ i ][ j ] 为 O，且 vis[ i ][ j ] 为 true，说明这个 O 和边界的 O 相连，不需要修改；

c. 如果 board[ i ][ j ] 为 X，不需要做任何处理。

非递归：

class Solution {
public:
    int dx[4]={0,0,1,-1};
    int dy[4]={1,-1,0,0};
    int m,n;
    void solve(vector<vector<char>>& board) {
        m=board.size(),n=board[0].size();

        vector<vector<bool>> vis(m,vector<bool>(n));

        for(int i=0;i<n;i++)
        {
            if(board[0][i]=='O' && !vis[0][i])//第一行
                SetVisO(board,vis,0,i);
            if(board[m-1][i]=='O' && !vis[m-1][i])//最后一行
                SetVisO(board,vis,m-1,i);
        }

        for(int i=1;i<m-1;i++)
        {
            if(board[i][0]=='O' && !vis[i][0])//第一列
                SetVisO(board,vis,i,0);
            if(board[i][n-1]=='O' && !vis[i][n-1])//最后一列
                SetVisO(board,vis,i,n-1);
        }

        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(board[i][j]=='O' && !vis[i][j])
                    board[i][j]='X';
            }
        }
    }
   
    //处理边界的O
    void SetVisO(vector<vector<char>>& board,vector<vector<bool>>& vis,int i,int j)
    {
        queue<pair<int,int>> q;
        q.push({i,j});
        vis[i][j]=true;//处理当前位置
        while(!q.empty())
        {
            auto [a,b]=q.front();
            q.pop();
            for(int k=0;k<4;k++)//处理上下左右位置
            {
                int x=a+dx[k],y=b+dy[k];
                if(x>=0 && x<m && y>=0 && y<n && board[x][y]=='O' && !vis[x][y])
                {
                    vis[x][y]=true;
                    q.push({x,y});
                }
            }
        }
    }
};

递归： 

class Solution {
public:
    int dx[4]={0,0,1,-1};
    int dy[4]={1,-1,0,0};
    int m,n;
    void solve(vector<vector<char>>& board) {
        m=board.size(),n=board[0].size();

        vector<vector<bool>> vis(m,vector<bool>(n));

        for(int i=0;i<n;i++)
        {
            if(board[0][i]=='O' && !vis[0][i])//第一行
                SetVisO(board,vis,0,i);
            if(board[m-1][i]=='O' && !vis[m-1][i])//最后一行
                SetVisO(board,vis,m-1,i);
        }

        for(int i=1;i<m-1;i++)
        {
            if(board[i][0]=='O' && !vis[i][0])//第一列
                SetVisO(board,vis,i,0);
            if(board[i][n-1]=='O' && !vis[i][n-1])//最后一列
                SetVisO(board,vis,i,n-1);
        }

        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(board[i][j]=='O' && !vis[i][j])//根据O的状态来判断是否修改
                    board[i][j]='X';
            }
        }
    }

    //处理边界的O
    void SetVisO(vector<vector<char>>& board,vector<vector<bool>>& vis,int i,int j)
    {
        vis[i][j]=true;
        for(int k=0;k<4;k++)
        {
            int x=i+dx[k],y=j+dy[k];
            if(x>=0 && x<board.size() && y>=0 && y<vis[0].size() && board[x][y]=='O'&&!vis[x][y])
                SetVisO(board,vis,x,y);
        }
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1708050.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【加密与解密（第四版）】第十四章笔记

【加密与解密（第四版）】第十四章笔记

第十四章 漏洞分析技术 14.1 软件漏洞原理 缓冲区溢出漏洞&#xff1a;栈溢出 堆溢出、整型溢出&#xff08;存储溢出、计算溢出、符号问题&#xff09; UAF&#xff08;Use-After-Free&#xff09;漏洞 14.2 ShellCode 功能模块&#xff1a;下载执行、捆绑、反弹shell 14.3 …
阅读更多...
采用java语言＋B/S架构＋后端SpringBoot前端Vue开发的ADR药品不良反应智能监测系统源码

采用java语言＋B/S架构＋后端SpringBoot前端Vue开发的ADR药品不良反应智能监测系统源码

采用java语言&#xff0b;B/S架构&#xff0b;后端SpringBoot前端Vue开发的ADR药品不良反应智能监测系统源码 ADR监测引擎每日主动获取检验数据、病历内容&#xff08;可拓展&#xff09;、以及其他临床数据&#xff0c;根据知识库内容自动判定患者是否有不良反应迹象&#xf…
阅读更多...
kettle组件之java代码，快速上手必看

kettle组件之java代码，快速上手必看

我们先了解不同于java代码的kettle的一些方法 1、getRow()&#xff1b; 获取每一行数据&#xff0c;循环读数据&#xff1b;返回的是Object[]数组 2、get(Fields.in,"字段名"); 获取具体的某个字段的名称 3、get(Fields.in,"字段名").getString(r); …
阅读更多...
【软考】下篇 第15章 面向服务架构设计理论与实践

【软考】下篇 第15章 面向服务架构设计理论与实践

目录 一、SOA定义二、微服务微服务优势微服务与SOA对比微服务架构模式方案微服务设计约束 三、SOA参考架构四、SOA设计的标准要求五、SOA设计原则六、SOA设计模式七、SOA实施 一、SOA定义 面向服务的体系结构 (Service-Oriented Architecture,SOA), 从应用和原理的角度看&…
阅读更多...
网络原理-HTTPS协议

网络原理-HTTPS协议

在前面说到HTTP中,我们通过抓包,可以看到许多信息内容,其中往往会包含一些敏感信息,这些都是明文传输,当我们的请求被黑客或者不法分子截获后,那就很危险了,因此衍生出了HTTPS协议来对传输数据进行加密。 一、加密原理 基本原理如下&#xff1a; 明文 密钥 > 密文 密文…
阅读更多...
线性稳压电路和开关稳压电路

线性稳压电路和开关稳压电路

稳压二极管稳压电路 电网电压增大&#xff0c;导到u1端的电压增大&#xff0c;从而使输出电压&#xff0c;稳压二极管两端的电压增大&#xff0c;稳压二极管两端电压增大&#xff0c;使流过的电注增大。那么&#xff0c;流过线性电阻R的总电流增大。 Ur电压增大&#xff0c;从…
阅读更多...
网络故障排除—NAT-源进源出

网络故障排除—NAT-源进源出

多网络双出口一边是运营商A,一边是运营商B&#xff0c;将内网服务器分别映射到运营商B和运营商A出口。查了保证内部上网用户网速快管理员开启了运营商选路功能&#xff0c;运营商B的网站从运营商B出去&#xff0c;然后写有两条等价默认路由分别指向两个外网出口。营商A的网站从…
阅读更多...
内网安全-隧道搭建穿透上线内网穿透-nps自定义上线内网渗透-Linux上线-cs上线Linux主机

内网安全-隧道搭建穿透上线内网穿透-nps自定义上线内网渗透-Linux上线-cs上线Linux主机

目录 内网安全-隧道搭建&穿透上线内网穿透-nps-自定义-上线NPS工具介绍搭建过程 nps原理介绍MSF上线CS上线 内网渗透-Linux上线-cs上线Linux主机1.下载插件2.导入插件模块3.配置监听器4.服务端配置5.配置C2监听器并生成木马6.执行木马 内网安全-隧道搭建&穿透上线 内网…
阅读更多...
重学java 49 增强for

重学java 49 增强for

知之俞明&#xff0c;则行之越笃&#xff1b;行之愈笃&#xff0c;则知之愈益&#xff1b; —— 24.5.28 一、基本使用 1.作用: 遍历集合或者数组 2.格式: for(元素类型 变量名:要遍历的集合名或者数组名) 变量名就是代表的每一个元素 3.快捷键: 集合名或者数组名.for package …
阅读更多...
Transformers x SwanLab：可视化NLP模型训练

Transformers x SwanLab：可视化NLP模型训练

HuggingFace 的 Transformers 是目前最流行的深度学习训框架之一&#xff08;100k Star&#xff09;&#xff0c;现在主流的大语言模型&#xff08;LLaMa系列、Qwen系列、ChatGLM系列等&#xff09;、自然语言处理模型&#xff08;Bert系列&#xff09;等&#xff0c;都在使用T…
阅读更多...
Web3探索加密世界：空投常见类型有哪些？附操作教程

Web3探索加密世界：空投常见类型有哪些？附操作教程

每种空投类型都有独特的特征和目的&#xff0c;我们需要了解不同类型的加密空投。本文给大家介绍的是流行的加密货币空投类型&#xff0c;以及一般空投是如何做的。感兴趣的话请看下去。 一、空投常见类型 1、持有者空投 持有者空投向钱包中持有一定数量数字货币的人免费发放…
阅读更多...
基于MyBatisPlus表结构维护工具

基于MyBatisPlus表结构维护工具

SuperTable表结构维护工具 一、简述 用于同步表实体与数据库表结构&#xff0c;同步建表、删改字段、索引&#xff0c;种子数据的工具… 一、开发环境 JDK&#xff1a;JDK8SpringBoot&#xff1a;2.7.2MyBatisPlus: 3.5.6MySQL: 5.7其他依赖&#xff1a;略 二、特性 表结…
阅读更多...
大话C语言：第18篇 函数

大话C语言：第18篇 函数

1 函数概述 函数是c语言的功能单位&#xff0c;实现一个功能可以封装一个函数来实现。函数是一种可重用的代码块&#xff0c;用于执行特定任务或完成特定功能。函数主要作用是对具备相同逻辑的代码进行封装&#xff0c;提高代码的编写效率&#xff0c;实现对代码的重用。例如&a…
阅读更多...
【Spring】深入学习AOP编程思想的实现原理和优势

【Spring】深入学习AOP编程思想的实现原理和优势

【切面编程】深入学习AOP编程思想的实现原理和优势 前言AOP的由来及AOP与代理的关系AOP的实现方式详解静态代理动态代理 AOP的应用场景记录日志权限控制数据库事务控制缓存处理异常处理监控管理 AOP的底层实现全流程解析Spring AOP的简介动态代理的实现原理Spring AOP的实现原理…
阅读更多...
流水账（CPU设计实战）——lab3

流水账（CPU设计实战）——lab3

Lab3 Rewrite V1.0 版本控制 版本描述V0V1.0相对V0变化&#xff1a; 修改了文件名&#xff0c;各阶段以_stage结尾&#xff08;因为if是关键词&#xff0c;所以module名不能叫if&#xff0c;遂改为if_stage&#xff0c;为了统一命名&#xff0c;将所有module后缀加上_stage&a…
阅读更多...
关于Windows中桌面窗口管理器的知识，看这篇文章就可以了

关于Windows中桌面窗口管理器的知识，看这篇文章就可以了

序言 你打开了任务管理器，发现了一个叫做“桌面窗口管理器”的东西，它是恶意软件吗？它应该在任务管理器吗？如果它应该在那里，它的作用什么？以下是你需要了解的所有信息。 什么是桌面窗口管理器 Desktop Window Manager（dwm.exe）是一个合成窗口管理器，可以在Windows…
阅读更多...
SB-OSC，最新的 MySQL Schema 在线变更方案

SB-OSC，最新的 MySQL Schema 在线变更方案

目前主流的 MySQL 在线变更方案有两个&#xff1a; 基于 trigger 的 pt-online-schema-change基于 binlog 的 gh-ost 上周 Sendbird 刚开源了他们的 MySQL Schema 在线变更方案 SB-OSC: Sendbird Online Schema Change。 GitHub 上刚刚 25 颗星星&#xff0c;绝对新鲜出炉。 …
阅读更多...
Java | Leetcode Java题解之第104题二叉树的最大深度

Java | Leetcode Java题解之第104题二叉树的最大深度

题目&#xff1a; 题解&#xff1a; class Solution {public int maxDepth(TreeNode root) {if (root null) {return 0;}Queue<TreeNode> queue new LinkedList<TreeNode>();queue.offer(root);int ans 0;while (!queue.isEmpty()) {int size queue.size();wh…
阅读更多...
go语言基准测试Benchmark 最佳实践-冒泡排序和快速排序算法基准测试时间复杂度对比

go语言基准测试Benchmark 最佳实践-冒泡排序和快速排序算法基准测试时间复杂度对比

在go语言中Benchmark基准测试( 在后缀为_test.go的文件中&#xff0c;函数原型为 func BenchmarkXxx(b *testing.B) {}的函数 )可以用来帮助我们发现代码的性能和瓶颈&#xff0c; 其最佳实践 应该是我们最常用的 冒泡排序和快速排序的测试了&#xff0c;废话不说&#xff0c;直…
阅读更多...
RDD实战：过滤算子 - filter()

RDD实战：过滤算子 - filter()

阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023